A wire in the form of a circular loop of radius 10cm lies in a plane normal to a magnetic field of 100T. If this wire is pulled to take a square shape in the same plane in 0.1s, find the average induced emf in the loop.
To solve the problem of finding the average induced emf in the loop, we can follow these steps:
Step 1: Calculate the initial area of the circular loop
The area A of a circular loop is given by the formula:
A=πr2
where r is the radius of the loop. Given that the radius r=10cm=0.1m:
A=π(0.1)2=π(0.01)=0.01πm2
Step 2: Calculate the final area of the square loop
Since the length of the wire remains constant, we can find the side length A of the square loop. The circumference of the circular loop is equal to the perimeter of the square:
2πr=4a
Thus, we can solve for a:
a=2πr4=πr2
Substituting r=0.1m:
a=π(0.1)2=0.1π2=0.05πm
Now, the area As of the square is:
As=a2=(0.05π)2=0.0025π2m2
Step 3: Calculate the change in magnetic flux
The magnetic flux Φ is given by:
Φ=B⋅A
where B is the magnetic field strength. The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=B⋅As−B⋅A
Substituting the values:
ΔΦ=100⋅(0.0025π2)−100⋅(0.01π)
Calculating each term:
ΔΦ=100⋅0.0025π2−100⋅0.01π
=0.25π2−1π
Now, we can approximate π≈3.14:
ΔΦ≈0.25(3.142)−1(3.14)≈0.25(9.86)−3.14≈2.465−3.14≈−0.675Wb
Step 4: Calculate the average induced emf
The average induced emf E is given by Faraday's law:
E=−ΔΦΔt
Given that Δt=0.1s:
E=−−0.6750.1=6.75V
Final Answer
The average induced emf in the loop is approximately:
E≈6.75V
---
The area A of a circular loop is given by the formula:
A=πr2
where r is the radius of the loop. Given that the radius r=10cm=0.1m:
A=π(0.1)2=π(0.01)=0.01πm2
Since the length of the wire remains constant, we can find the side length A of the square loop. The circumference of the circular loop is equal to the perimeter of the square:
2πr=4a
Thus, we can solve for a:
a=2πr4=πr2
Substituting r=0.1m:
a=π(0.1)2=0.1π2=0.05πm
Now, the area As of the square is:
As=a2=(0.05π)2=0.0025π2m2
The magnetic flux Φ is given by:
Φ=B⋅A
where B is the magnetic field strength. The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=B⋅As−B⋅A
Substituting the values:
ΔΦ=100⋅(0.0025π2)−100⋅(0.01π)
Calculating each term:
ΔΦ=100⋅0.0025π2−100⋅0.01π
=0.25π2−1π
Now, we can approximate π≈3.14:
ΔΦ≈0.25(3.142)−1(3.14)≈0.25(9.86)−3.14≈2.465−3.14≈−0.675Wb
The average induced emf E is given by Faraday's law:
E=−ΔΦΔt
Given that Δt=0.1s:
E=−−0.6750.1=6.75V
The average induced emf in the loop is approximately:
E≈6.75V
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.24videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.34videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A wire of length l in the from of a circular loop lies in a plane normal to a magnetic firld B0 . If this wire is converted into a square loop in time t0 , find the average induced emf.
View SolutionA wire of length l in the form of a square loop lies in a plane normal to a magnetic field B0. If this wire is converted into a circular loop in time, then find the average induced emf.
View Solution
Knowledge Check
- Question 1 - Select One
A circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
AπBr2t(1−π2)BπBr2t(1−π3)CπBr2t(1−π4)DπBr2t(1−π5) - Question 2 - Select One
A given wire is bent into a circular loop of radius 7cm and is placed perpendicular to a magnetic field of 1.0T.Within 0.1 second ,the loop is changed to a 100cm square and the field increases to 1.8T .The induced emf in the coil will be
A13mVB26mVC39mVD52mV - Question 3 - Select One
The figure shows a uniform, 3.0 T magnetic field that is normal to the plane of a conducting, circular loop with a resistance of 1.5 Ω and a radius of 0.024 m. The magnetic field is directed out of the paper as shown . Note: The area of the non-circular portion of the wire is considered negligible compared to that of the circular loop.
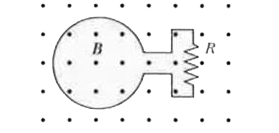
If the magnetic field is held constant at 3.0 T and the loop is pulled out of the region that contains the field in 0.2 s, what is the magnitude of the average induced emf in the loop?A2.7×10−2VB6.4×10−2VC9.8×10−2VD5.4×10−2V
A conducing circular loop having a radius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
View SolutionA circular loop of radius 0⋅2m carrying a current of 1A is placed in a uniform magnetic field of 0⋅5T. The magnetic field is perpendicular to the plane of the loop. What is the force experienced by the loop?
View SolutionA conducing circular loop is placed in a uniform magnetic field of 0.02 T, woth its plane perpendicular to the field. If the redius of the loop starts shrinking at a constant rate of 1.0mm/s, then find the emf induced in the loop, at the instant when radius is 4 cm.
View SolutionA square loop of side 44 cm is changed to a circle in time 0.5 sec with its plane normal to a magnetic field 0.6 T. The emf induced is
View SolutionA square loop of side 22cm is changed to a circle in time 0.4sec with its plane normal to a magnetic field 0.2T. The emf induced is
View Solution

