A rod of length 3l rotated with an angular velocity ω as shown in figure. The unfiorm magnetic field B is into the paper. Find
(a) VA−VC (b) VA−VD
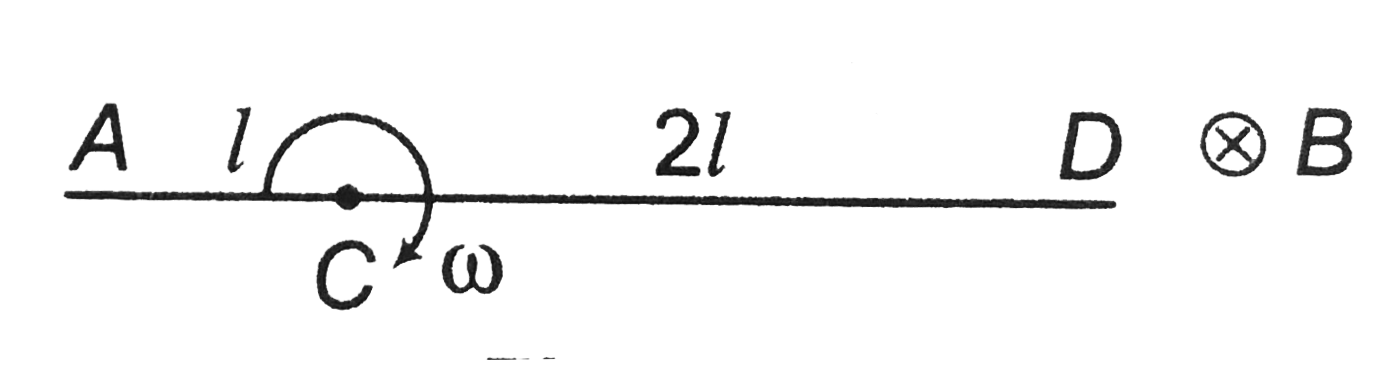
Bω(2l)24 Bω(2l)22 −3Bωl2/2
Bω(2l)22 Bω(2l)22 −3Bωl2/2
Bω(2l)22 Bω(2l)22 3Bωl2/2
Bω(2l)22 Bω(l)22 −3Bωl2/2
The correct Answer is:B
VA−VC=Bωl22
VD−VC=Bω(2l)22
From these two equations we find
VA−VD=−3Bωl2/2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.34videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.43videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.18videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
 View Solution
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating - Question 2 - Select One
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
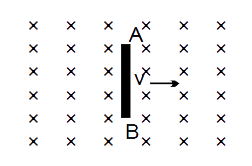 AThe rod becomes electrically chargedBThe end A becomes positively chargedCThe end B becomes positively chargedDThe rod becomes hot because of Joule heating
AThe rod becomes electrically chargedBThe end A becomes positively chargedCThe end B becomes positively chargedDThe rod becomes hot because of Joule heating - Question 3 - Select One
A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA conducting rod AC of length 4l is rotated about point O in a uniform magnetic field →B directed into the plane of the paper. AO=landOC=3l. Find VA−VC.
 View Solution
View SolutionIn the uniform electric field shown in figure, find :
a. VA−VD
b. VA−VC
c. VB−VD
d. VC−VD
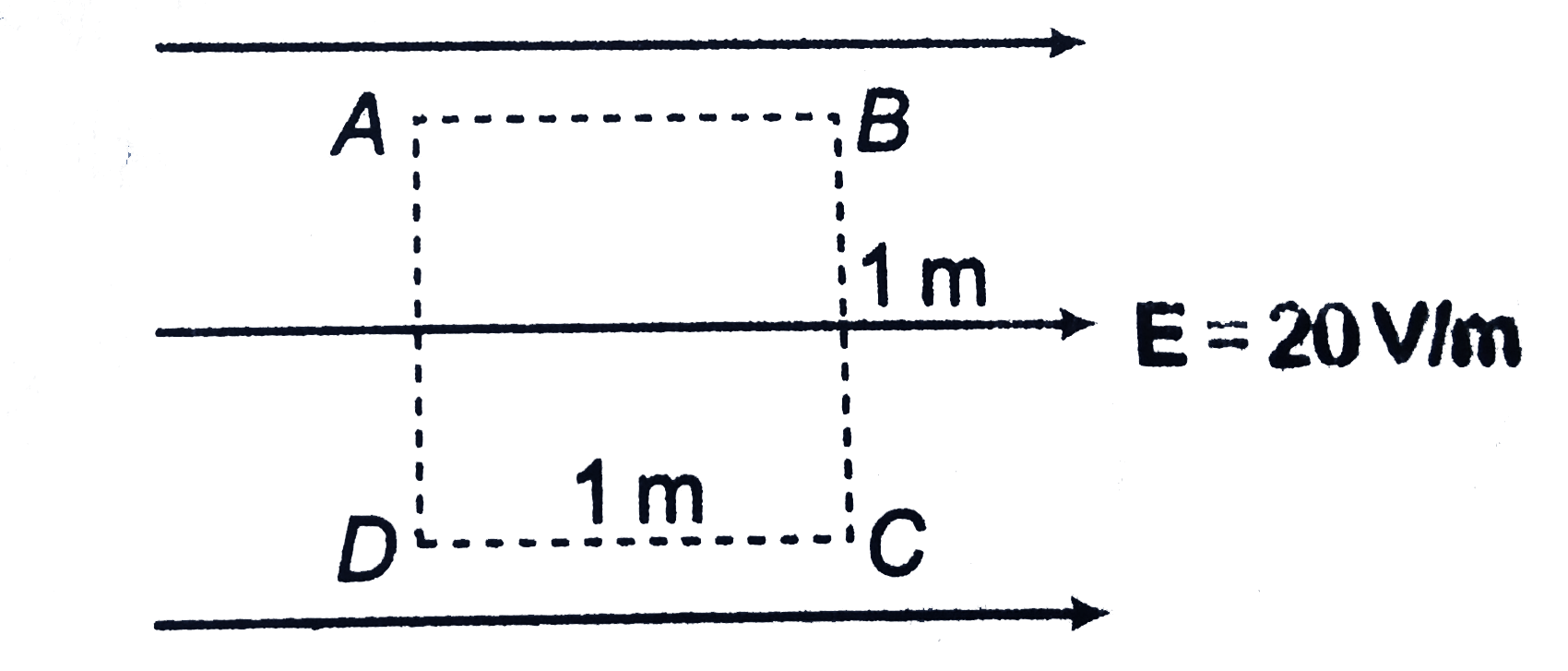 View Solution
View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
View SolutionIn the figure shown a T-shaped conductor moves with constant angular velocity ω in a plane perpendicular to uniform magnetic field B. The potential difference VA−VB is
 View Solution
View Solution

