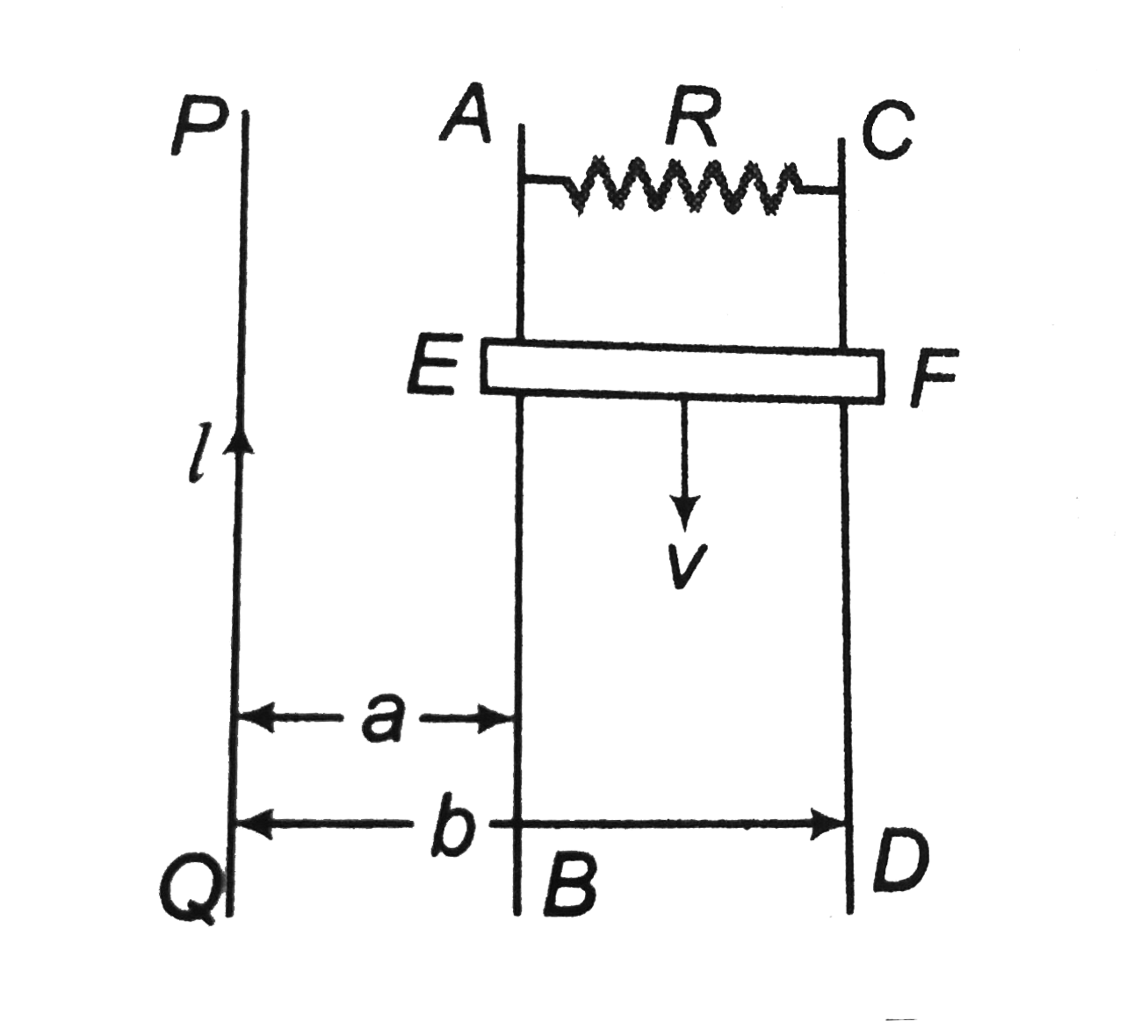
PQ is an infinite current carrying conductor. AB and CD are smooth conducting rods on which a conductor EF moves with constant velocity v as shown. The force needed to maintain constant speed of EF is
1VR[μ0IV2πln(b)a]2
vR[μ0IV2πln(a)b]2
vR[μ0IV2πln(b)a]2
None of these
The correct Answer is:A
Bx=μ02πIx
de=Bxvdx=μ02πIxvdx
e=∫badeμ0Iv2πln(ba)
i=eR=μ0Iv2πrln(ba)=induced current
dF=(i)(dx)Bx
[μ0Iv2πRln(ba)][μ02πIx]dx
F=∫badF
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Comprehension Based
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.
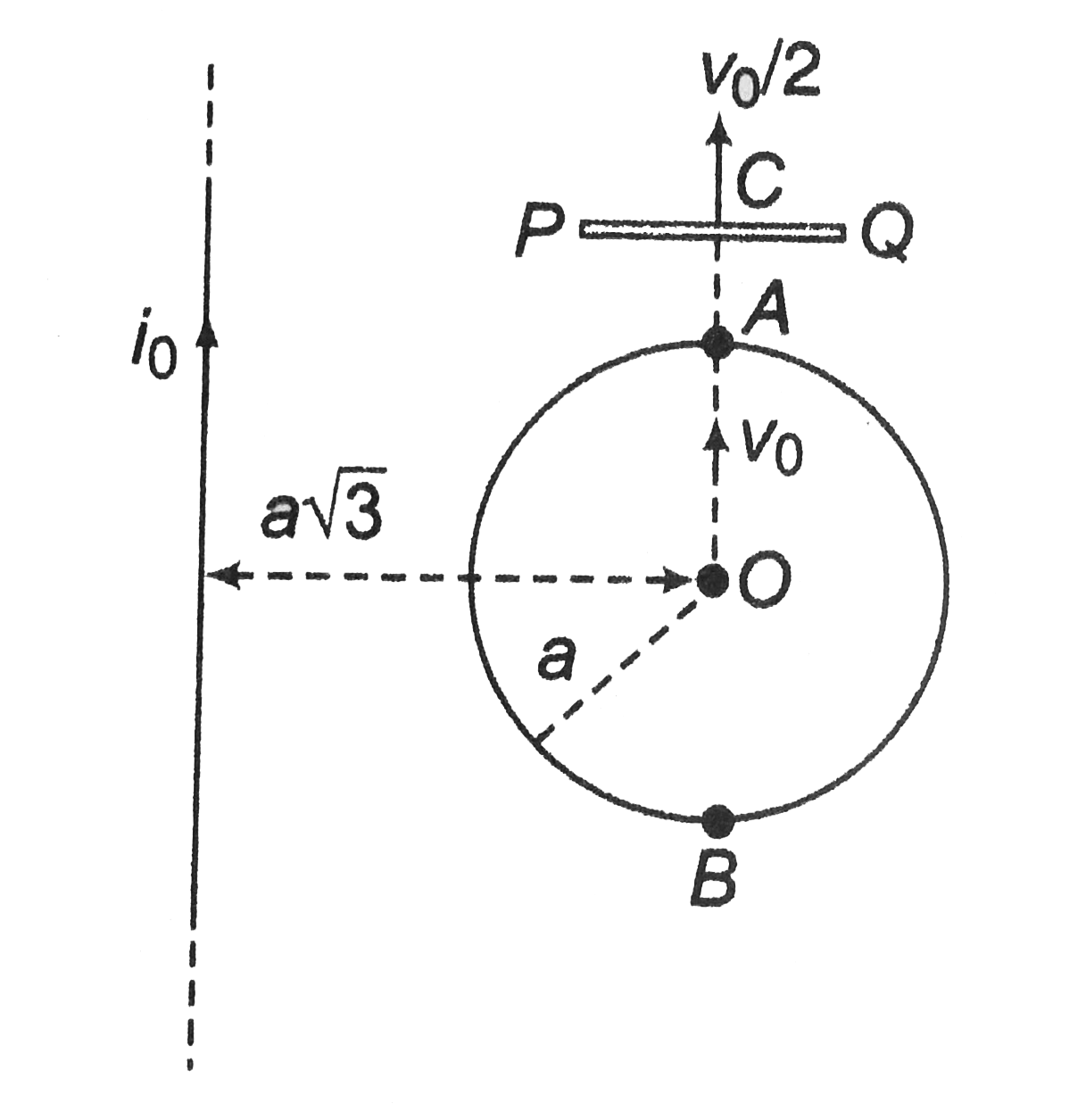
(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA conducting rod is moved with a constant velocity v in a magnetic field. A potential difference appears across the two ends
View Solution
Knowledge Check
40V A constant force →F is acting on a body of mass m makes it move with constant velocity →v as shown in the M figure. The power P exerted is
 AFcosθvBFcosθmgCFmgcosθvDmgsinθF
AFcosθvBFcosθmgCFmgcosθvDmgsinθF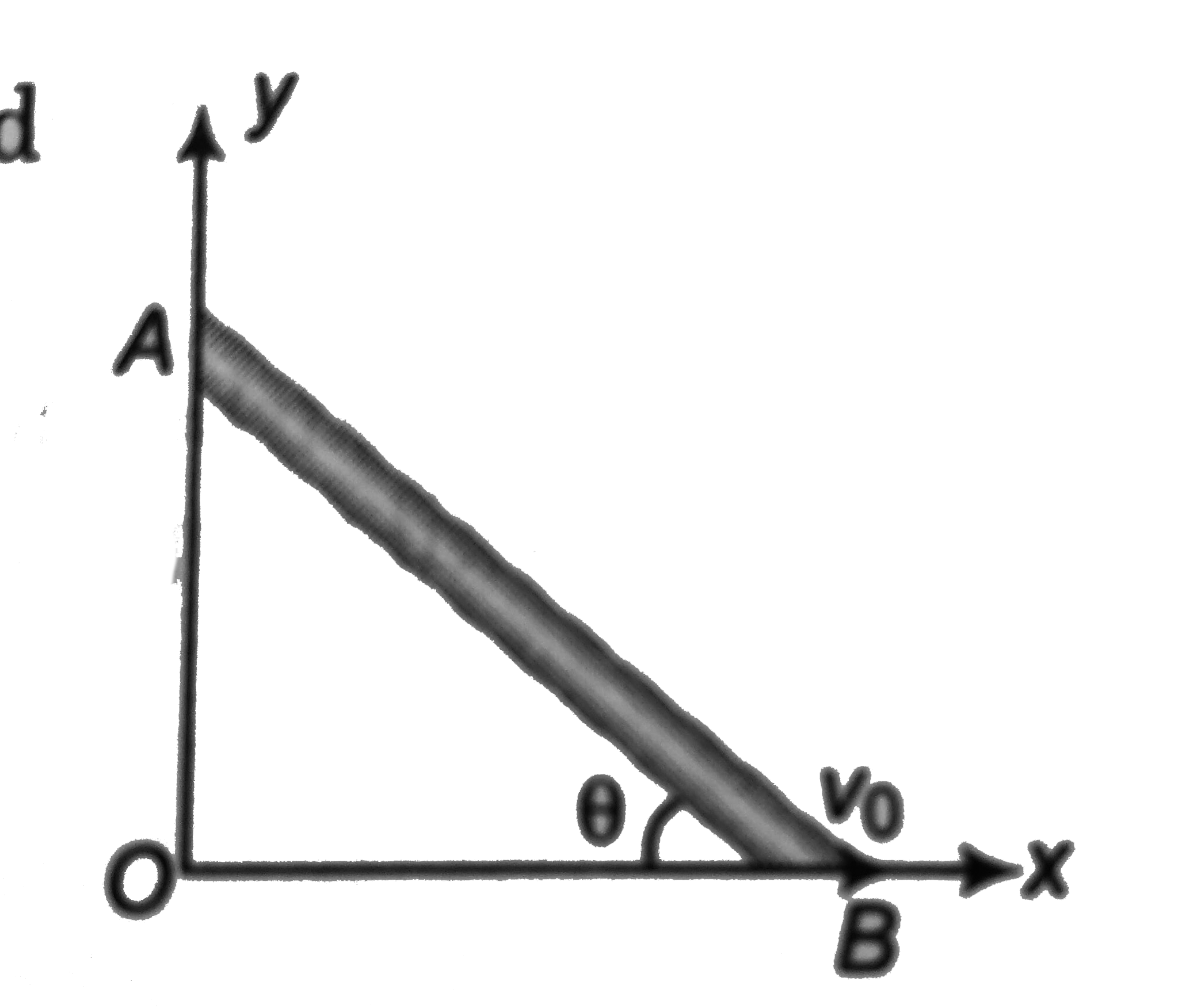
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.A conductor PQ , with PQ=r , moves with a velocity v in a uniform magnetic field of induced B . The emf induced in the rod is
A(→v×→B).→rB→v.(→r×→B)C→B.(→r×→v)D∣∣→r×(→v×→B)∣∣
In the above question find the force required to move the rod with constant velocity v, and also find the power delivered by the external agent.
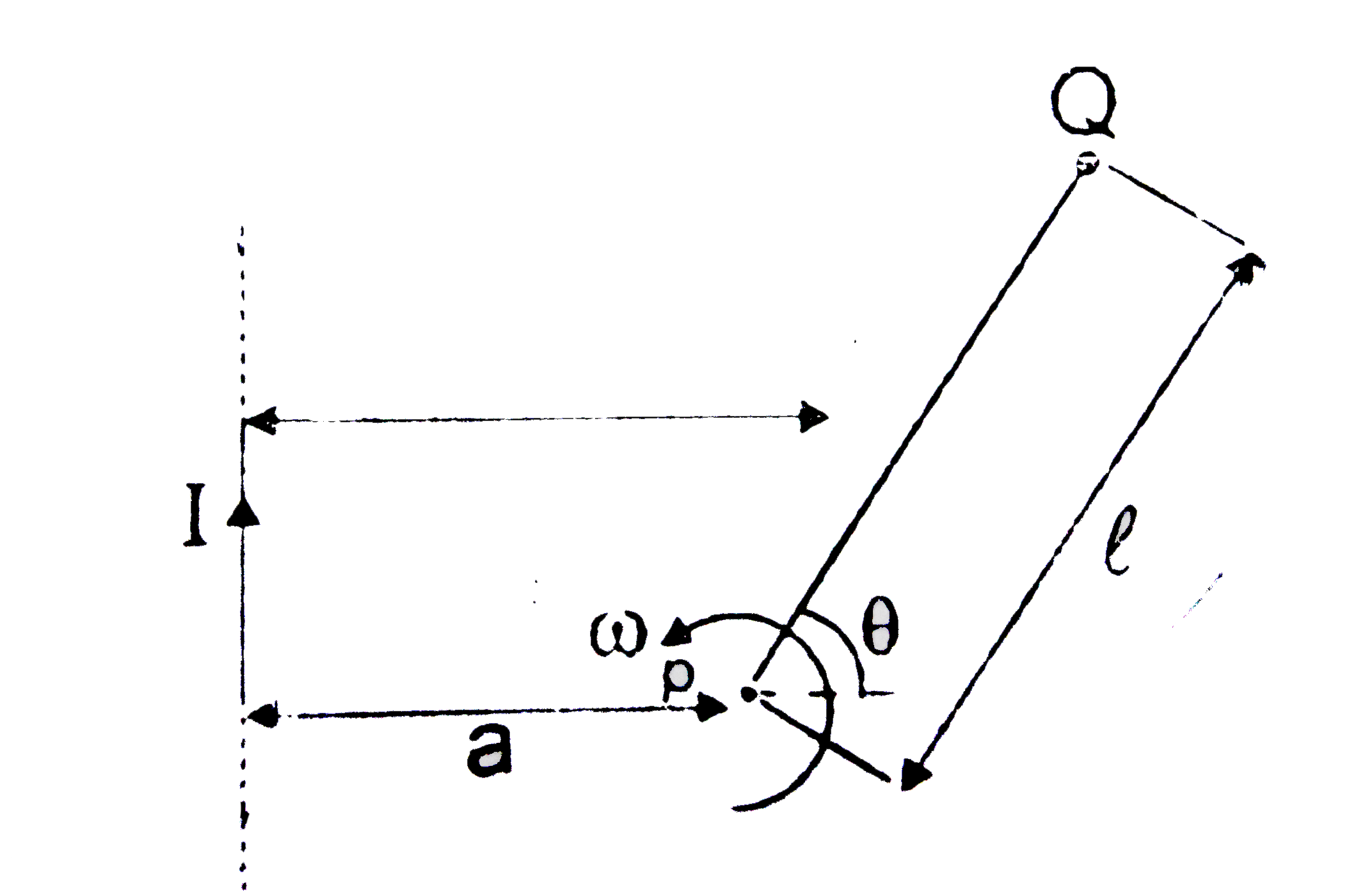
View SolutionIn the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.
View SolutionTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward with a constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
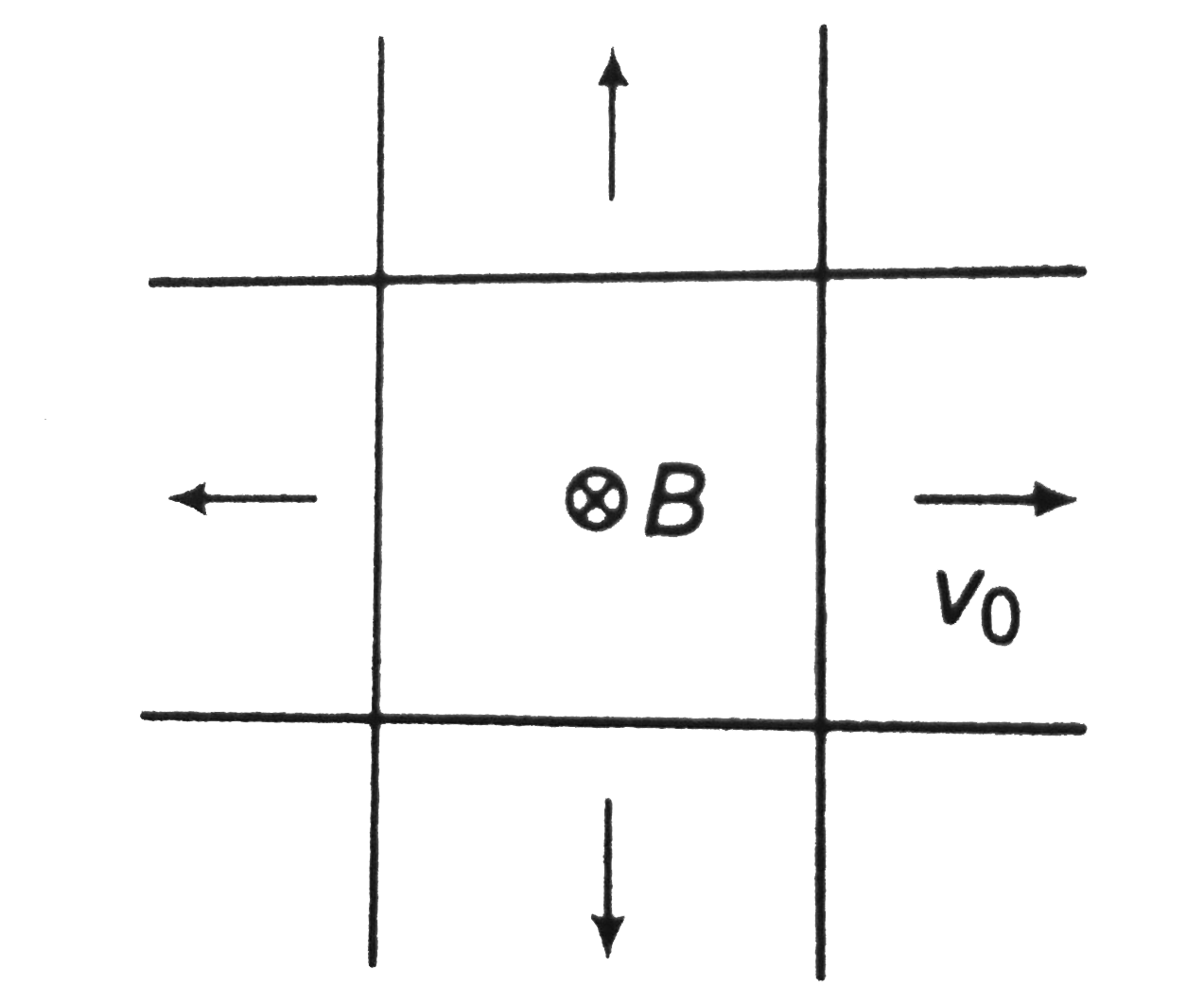
View Solution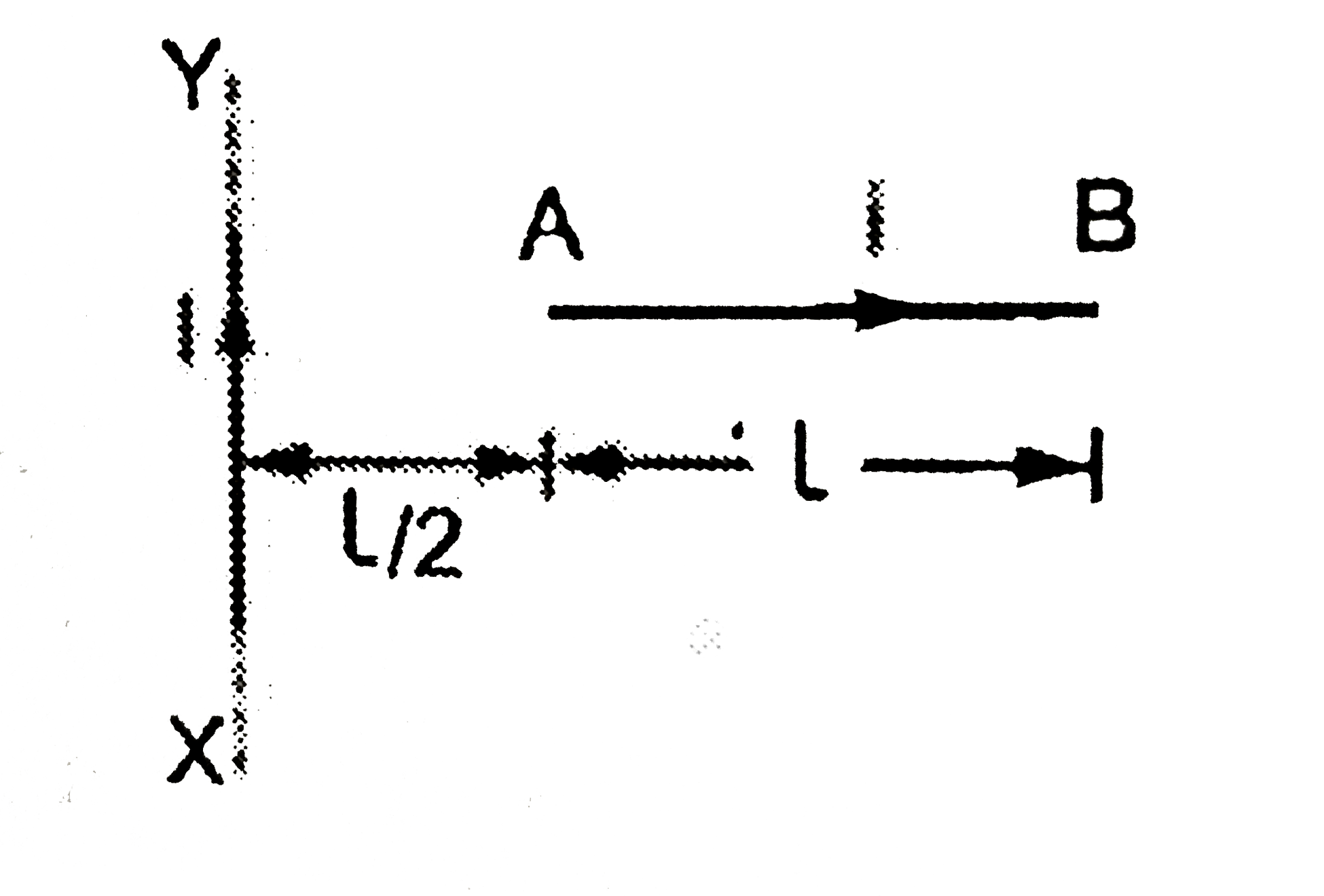
A conductor AB of length l carrying a current i is placed perpendicular to a long straight conductor XY carrying a current I, as shown. The force on AB will act
View SolutionA conducting rod of resistence r moves uniformely with a constant speed v. If the rod keeps moving uniformly, then the amount of force required is -
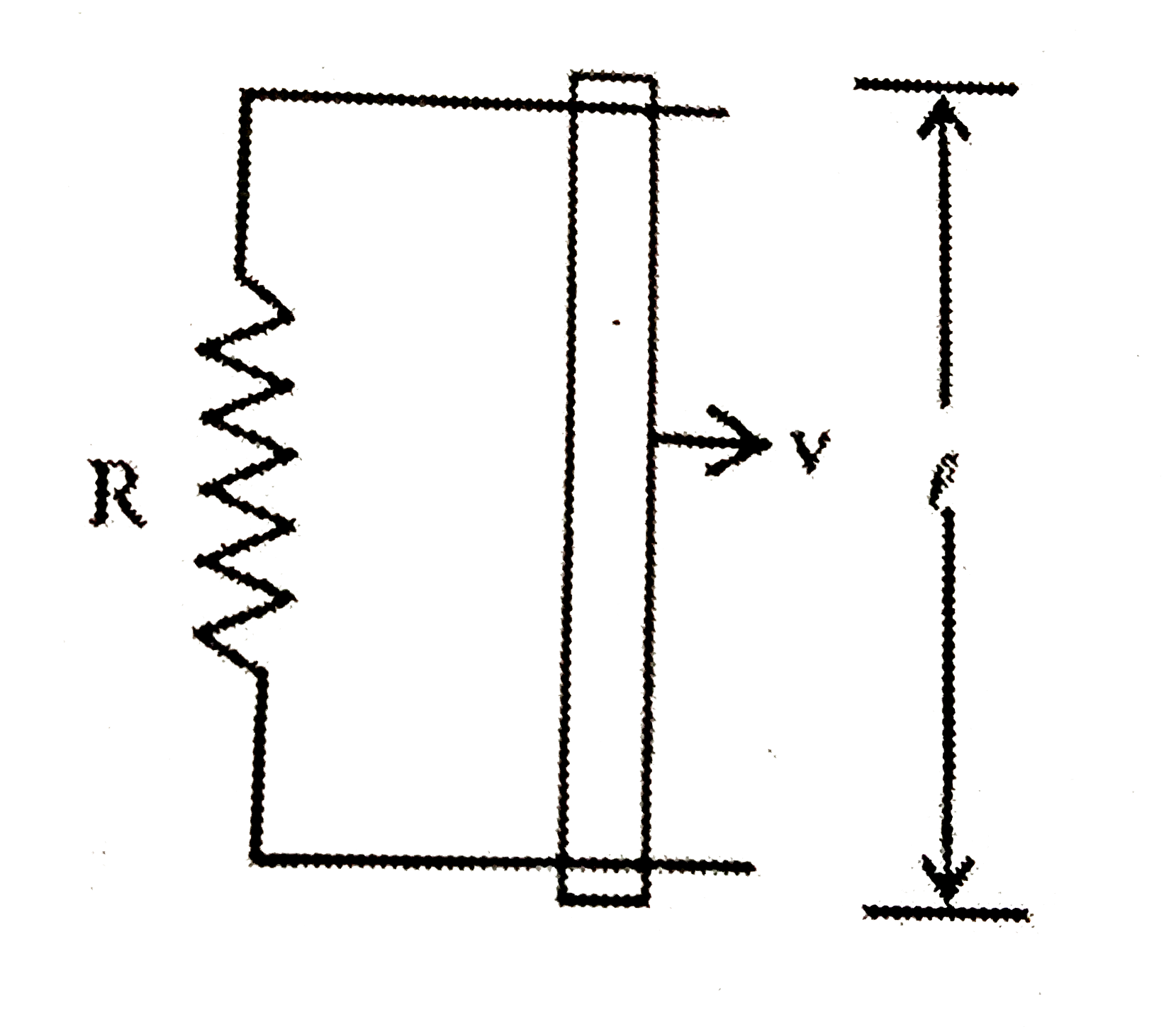
View Solution
