A conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
The correct Answer is:B, C
a. At the given instant
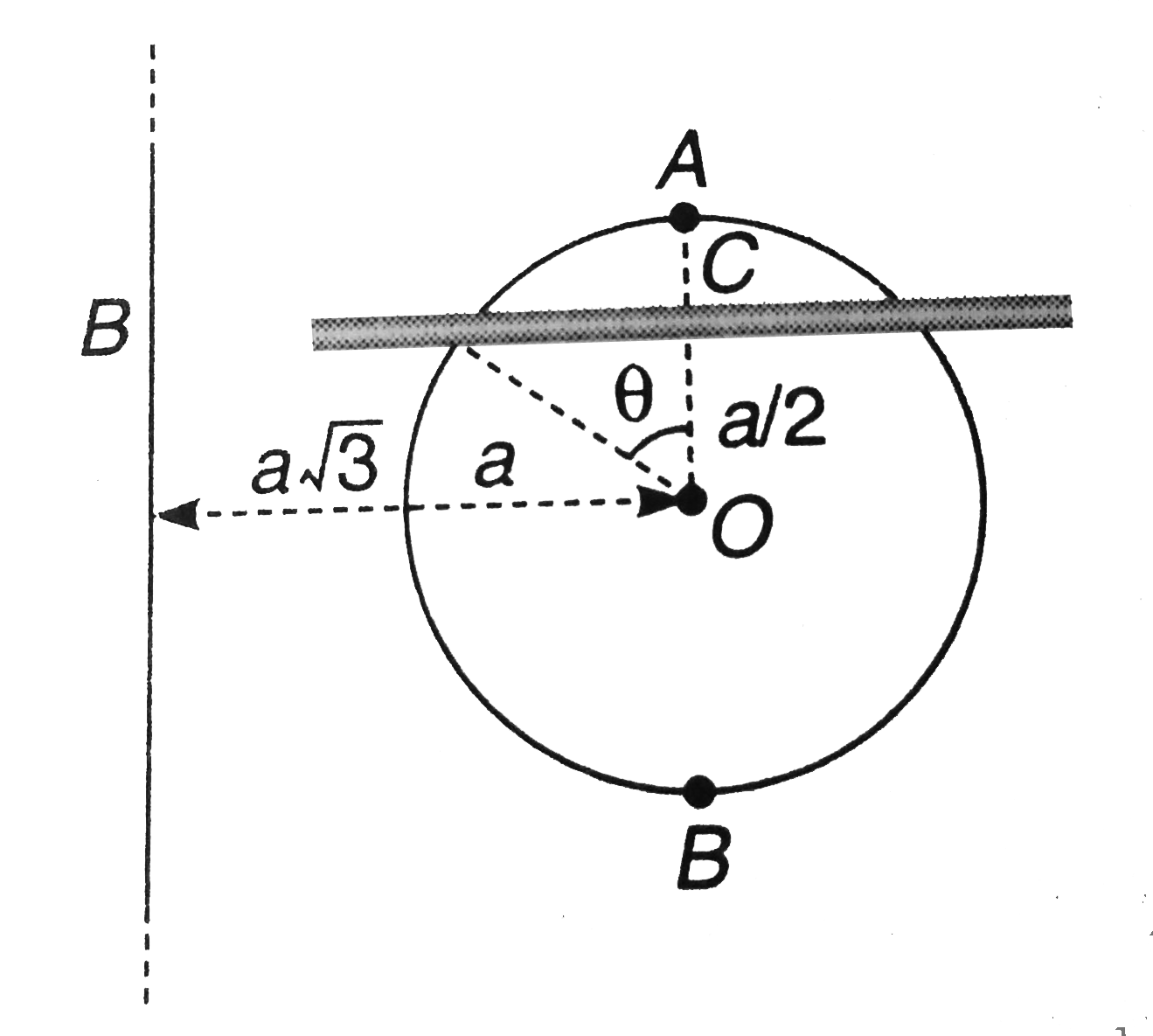
AC=a2,OC=a2
and cosθ=a2a=12,θ=π3
∴ Velocity of rod
=(+v02) along the direction of current.
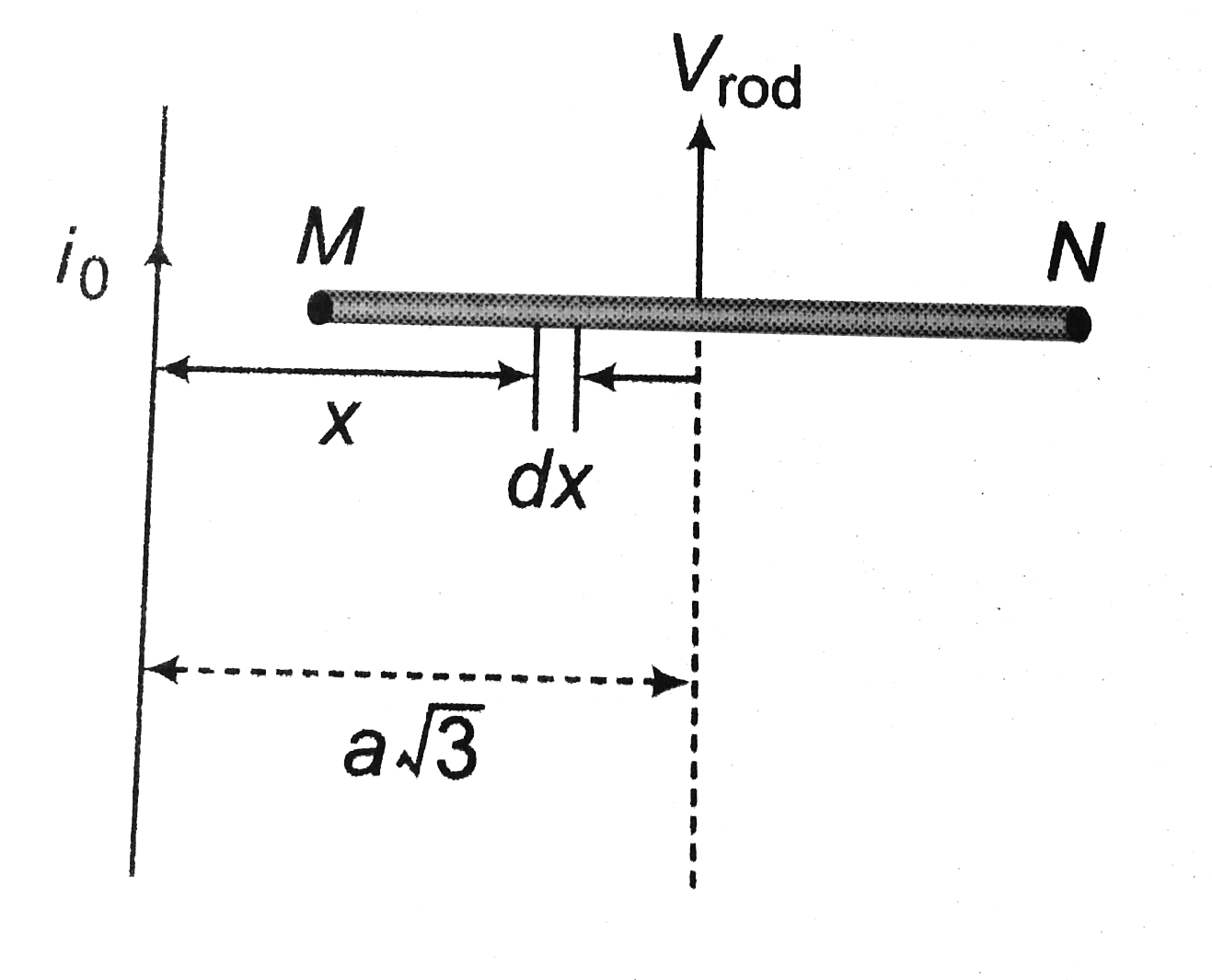
Emf induced across the ends M and N
Erod=∫a√3+a√32a√3−a√32vrodBdx
=vrod∫3a√32a√32μ0i02πxdx
(v02)μ0i02πln(31)
with end M at higher potential.
Since, the effective length of both the arcs MAN and MBN is MN.
∴EMAN=EMBN+Vloopμ0i02πln3
=v0μ0i02πlne
with point M at higher potential.
Resistance of arc MAN
⇒R1=(R)2(aθ)=2aRπ3
⇒ Resistance of arc MBN
⇒R2=(R)a(2π−2θ)=4aRπ3
Equivalent circuit at the given instant is shown in figure.

Current through the rod MN,
i=(i1+i2)=(EMAN−ErodR1)+(EMBN−RrodR2)
i=(EMAN−Erod)[1R1+1R1]
=(v0μ0i0)(ln304π)[912+14][3aRπ]
9v0i0μ016aRπ2ln(3)
b. Force on the rod

Frod=∫3a√32a√32B
=iμ0i02πln3=9μ20i20v032aRπ3(ln3)2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A small conducting loop of radius r & resistance R is pulled with velocity v perpendicular to long straight current carrying conductor carrying a current i. If the power dissipated (P ) in the loop is constant find the variation of the velocity of the loop with the displacement x.

View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
View Solution
Knowledge Check
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2RA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to LA small square loop of edge a and resistance R is moved with velocity v0 away from an infinitely long current carrying conductor carrying current I so that the conductor and side of square are always in same plane. Find induced current in loop at a separation of r
Aμ0ia2vπr2RBμ0ia2v4πr2RCμ0ia2v2πr2RDμ0iav2πrR
A circular conducting loop of radius R and resistance per unit length λ is pulled out from the regio of uniform magnetic filed with constant velocity v. The situation shown in the figure corresponds to that is at t=0. Mark out the correct statement (s)

View SolutionA conducting loop is pulled with a constant velocity towards a region of unifrom maganetic field of induction B as shown in the figure. Then the current involved in the loop is (d>r)
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is parallel to the plane of the loop. The magnetic torque acting on the loop is-
View SolutionA very long uniformly charged rod falls with a constant velocity V through the centre of a circular loop. Then the magnitude of induced emf in the loop is
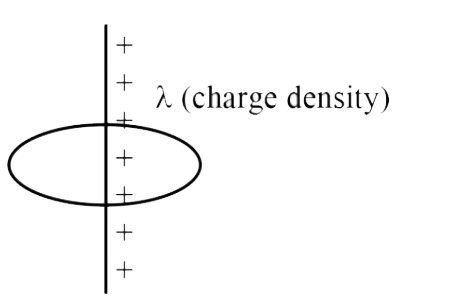
View SolutionA circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
View Solution
