Distance between two slits is d. Wavelength of light is λ. There is a
source of light S behind S2 at a distance D1. A glass slab of thickness t and
refractive index μ is kept in front of S1. Find.

(a) Net path difference at point P at an angular position θ.
(b) Write the equation for finding two angular positions corresponding to second order
minima (y2andy2').
If θ in part (b) does not come out to be small, then find two y-coordinates corresponding
to them.
(a) Δx1=SS1−SS2=(d/2)(d)D1
=d22D1(Using Δx=ydD)
Δx2=dsinθ
Δx3=(μ−1)t
∴Δxnet=(Δx1+Δx3)~dsinθ
={(d22D1+(μ−1)t}~dsinθ
(b) Corresponding to second order minima, net path difference should be 3λ2. So, let θ1andθ2 be
the two angular positions, then
{ d^2/(2D_1) + (mu-1)t} - dsin theta_1 = (3lambda)/2 <br> and d sin theta_2 -{d^2/(2D_1) + (mu - 1)t} = (3lambda)/ 2 <br>Fromthesetwoequations,wecanf∈dtheta_1 and theta_2.<br> (c) Even if theta is not small, we can write<br> tan theta = y/D_2<br> :. y= D_2tantheta <br> Therefore, two y-coordinates are <br> y_1 = D_2 tan theta_1 <br>and y_2 = D_2 tan theta_2 .
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 3
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - type-3
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 1
2 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
If v is the velocity of light in air or vacuum, find the time taken by the light to travel through a glass slab of thickness x and having refraction index μ.
View SolutionTwo parallel rays are travelling in a medium of refractive index μ1=43 . One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=32 The path difference between the two rays due to the glass slab will be
View Solution
Knowledge Check
A ray of light passes throught a plane glass slab of thickness t and refractive index μ=1.5. The angle between incident ray and emergent ray will be
A0∘B30∘C45∘D60∘In a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is
 A(a) Decreases by (μ−1)tB(b) Increases by (μ−1)tC(c) Does not changeD(d) Increases by μt
A(a) Decreases by (μ−1)tB(b) Increases by (μ−1)tC(c) Does not changeD(d) Increases by μtIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)
There is a large circle (not a screen this time) around two coherent
sources S−1 and S2 kept at a distance d=3.4λ.
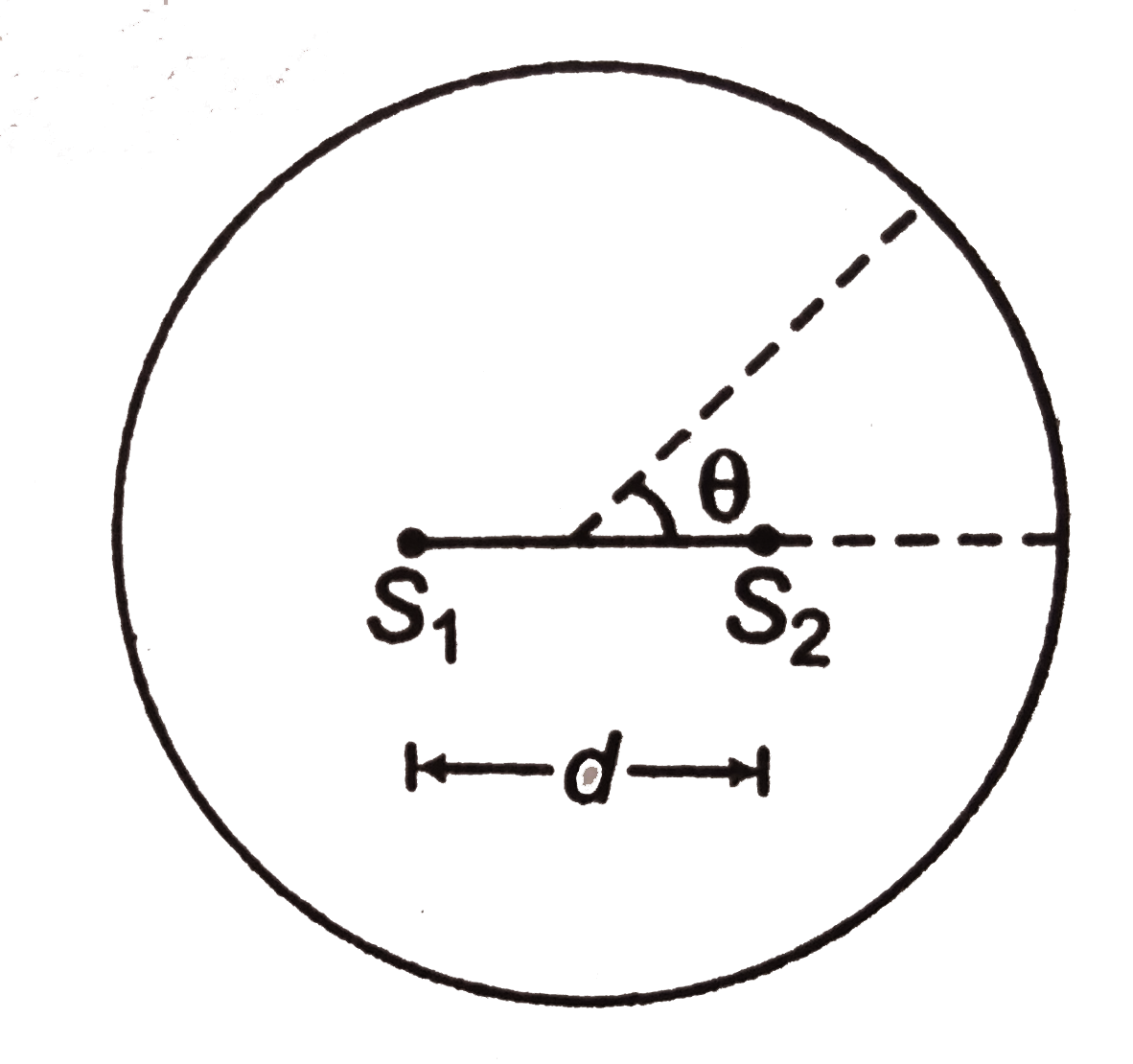
(a) Find total number of maximas on this circle.
(b) Four angular positions corresponding to third order maxima on this circle.
View SolutionA transparent slab of thickness t and refractive index μ is inserted in front of upper of YDSE apparauts. The wavelength of ligth used. is λ. Assume that there is no absorption of light by the slab. Mark the correct statement(s).
View SolutionIn the Young's double slit experiment , a mica slip of thickness t and refractive index μ is introduced in the ray from first source S1 . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
View SolutionA monochromatic light of λ=5000Å is inciden on two slits seperated by a distance of 5×10−4m. if a thin glass of thickness 1.5×10−6 m and refractive index 1.5 placed between one of the slits and screen. The pahses difference introduced at the position of central maxima is
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
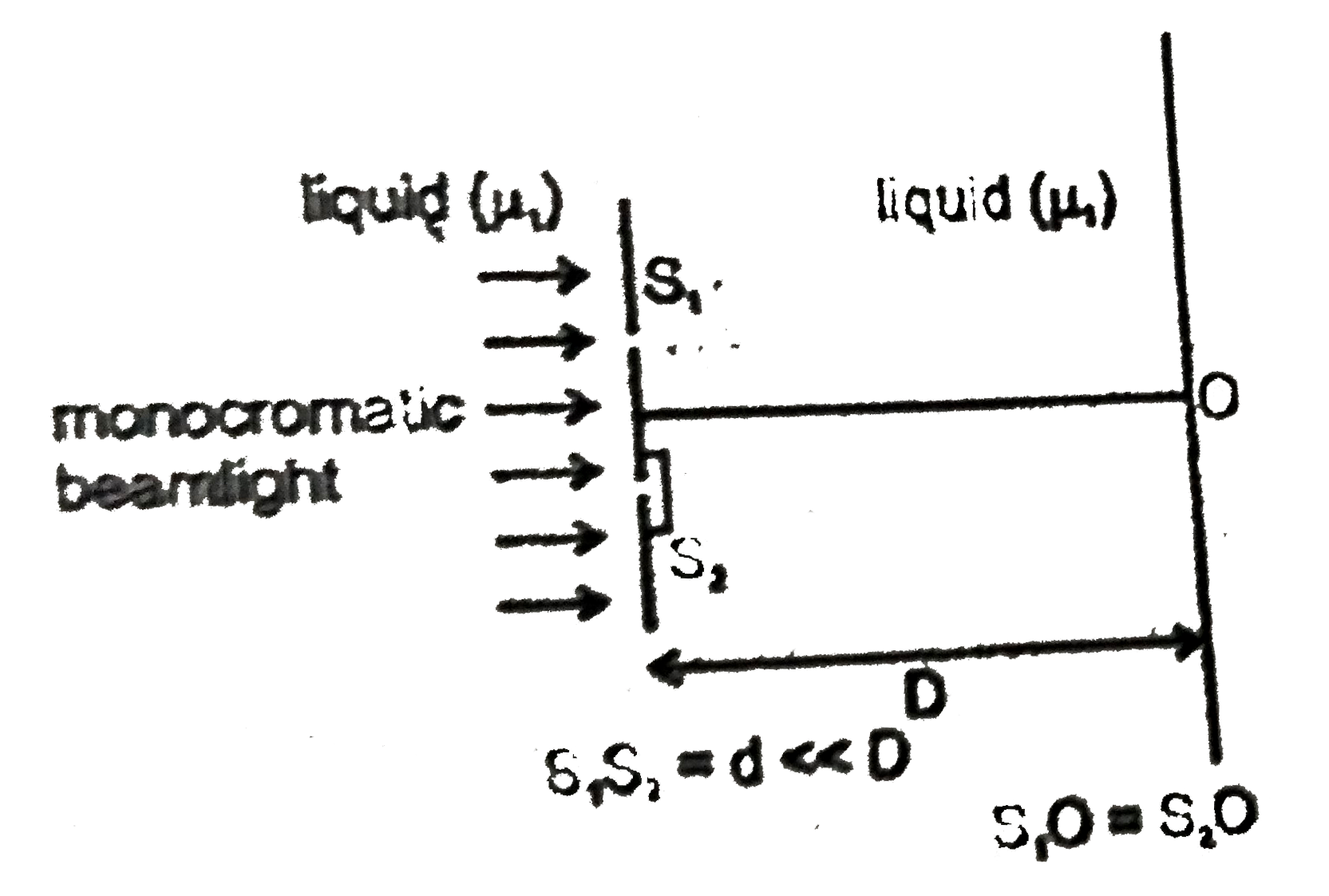
View Solution
