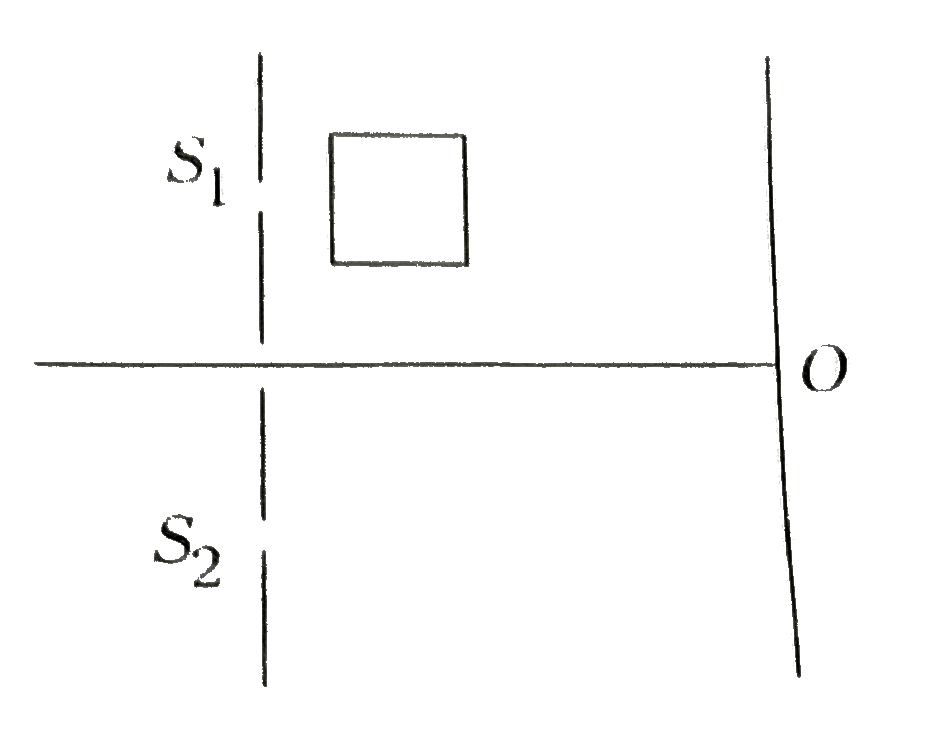
Assertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.

Reason: For 11th order maxima path difference should be more.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:D
At centre, path difference is maximum and this is
equal to S1S2. Then, path difference decreases as
we move away on the screen. So, order of fringe
also decreases. Hence, 11th order maxima occurs
before 10th order maxima.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Objective11videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question2videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.26videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions120videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
Assertion In the YDSE set up shown in figure a glass slab is inserted in front of the slit S1 as shown in figure Then zero order maxima (where path difference =0) will lie above point O.
Reason Glass slab will produce an extra path difference in the path of the ray passing through S1
 View Solution
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 isView Solution
Knowledge Check
- Question 1 - Select One
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circles - Question 2 - Select One
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpoints - Question 3 - Select One
Assertion: In the figure shown, zero order maxima will lie above point O.

Reason: Zero order maxima normally means a point where path difference is zero.A(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.B(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.C(c) If Assertion is true, but the Reason is false.D(d) If Assertion is false, but the Reason is true.
For nth order maxima in Fraunhoffer diffraction by a single slit, aperature, the value of path difference should be
View SolutionStatement I: Two point coherent sources of light S1 and S2 are placed on a line as shown in figure. P and Q are two points on that line. If at point P maximum intensity is observed, then maximum intensity should also be observed at Q.

Statement II: In figure the distance |S1P−S2P| is equal to distance |S1Q−S2Q|.View SolutionThree coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.
 View Solution
View SolutionTwo coherent sources of wavelength 6.2×10−7 m produce interference . The path difference corresponding to 10th order maximum will be ?
View SolutionAssertion: Distance between two coherent sources S1andS2 is 4λ. A large circle is drawn around these sources with centre of circle lying at centre of S1andS2. There are total 16 maxima on this circle.
Reason: Total number of minimas on this circle are less, compared to total number of maximas.View Solution

