A parallel beam of light $(λ = 5000 Å)$ is incident at an angle $θ = 30^{\circ}$ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I_0. Point O is equidistant from $S_{1} and S_{2}$ . The distance between slits is 1mm.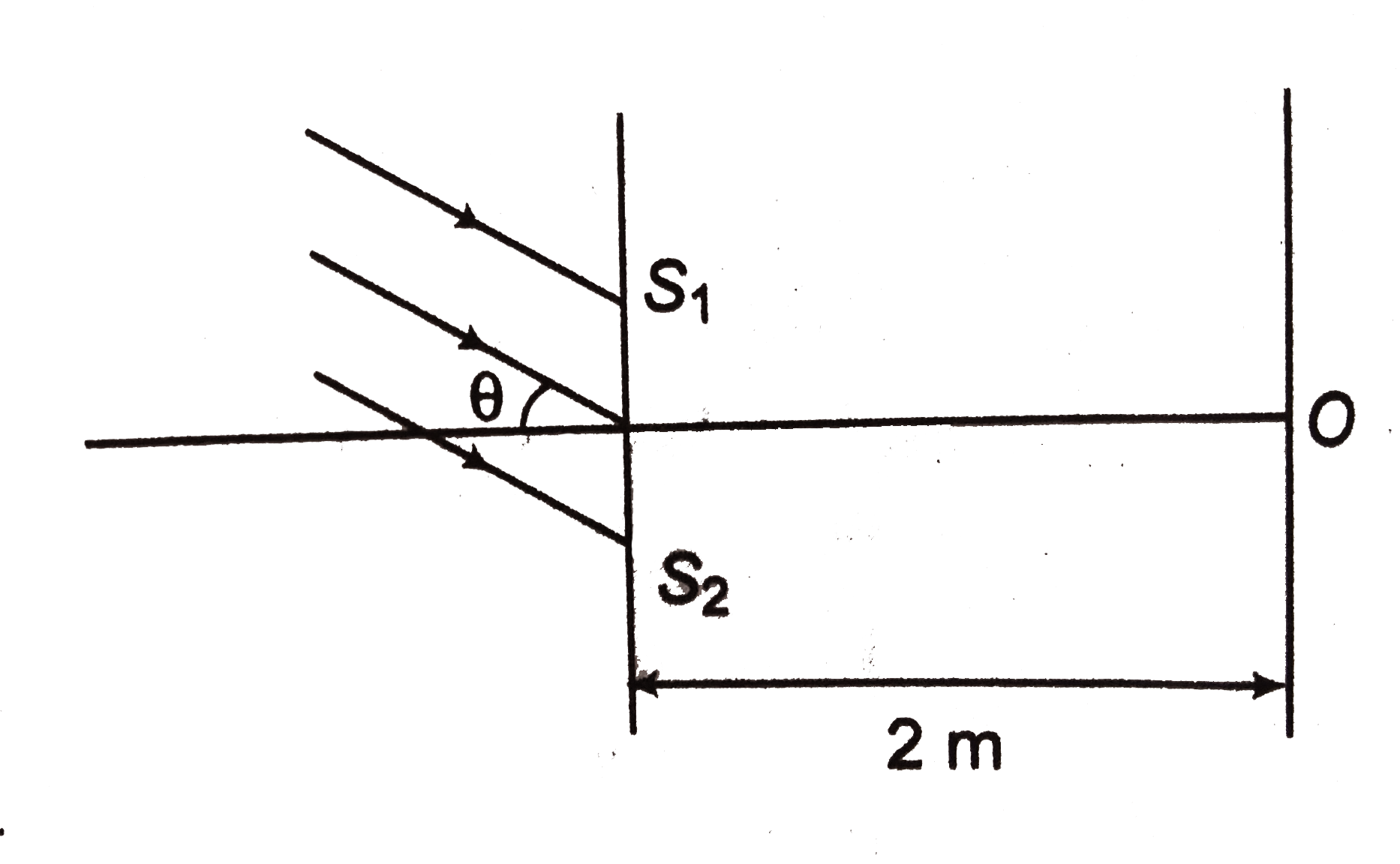

A

the intensity at P is $4 I_{0}$ .

B

The intensity at O is zero.

C

The intensity at a point on the screen 2mm above O is $4 I_{0}$ .

D

The intensity at a point on the screen 4 mm above O is zero.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$Δ x_{0} = d sin θ = (10^{- 3}) (\frac{1}{2})$
$= 5 \times 10^{- 4} m = (10^{3}) λ$
Since, $Δ x_{0}$ is integer multiple of $λ$ , it will produce
maximum intensity or $4 I_{0}$ at O.
$ω = \frac{λ D}{d} = \frac{(5 \times 10^{- 7}) (2)}{10^{- 3}}$
$= 10^{- 3} m = 1 m m$
At 4 mm, we will get 4th order maxima.

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A thin glass plate of thickness $t (= λ / 3, λ$ being the wavelength of incident light ) and refractive index $μ = 1.5$ is inserted between one of the slits and the screen in Young's double slit experiment. If the intensity at a point on the screen equidistance from the slit is i, then
Aintensity at the same point before introduction of glass plate was 31/2
Bintensity at the same point before introduction of glass plate was 41/3
Ccentral maximum will be in the lower half of screen after introduction of glass plate
Dshape of fringes will be straight line on the screen
Question 2 - Select One
In figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit $S_{1}$ passes through a medium of variable refractive index $μ = 1 + a x$ (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on $S_{1}$ . Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength $λ$ in air) is

A $\frac{λ}{l}$
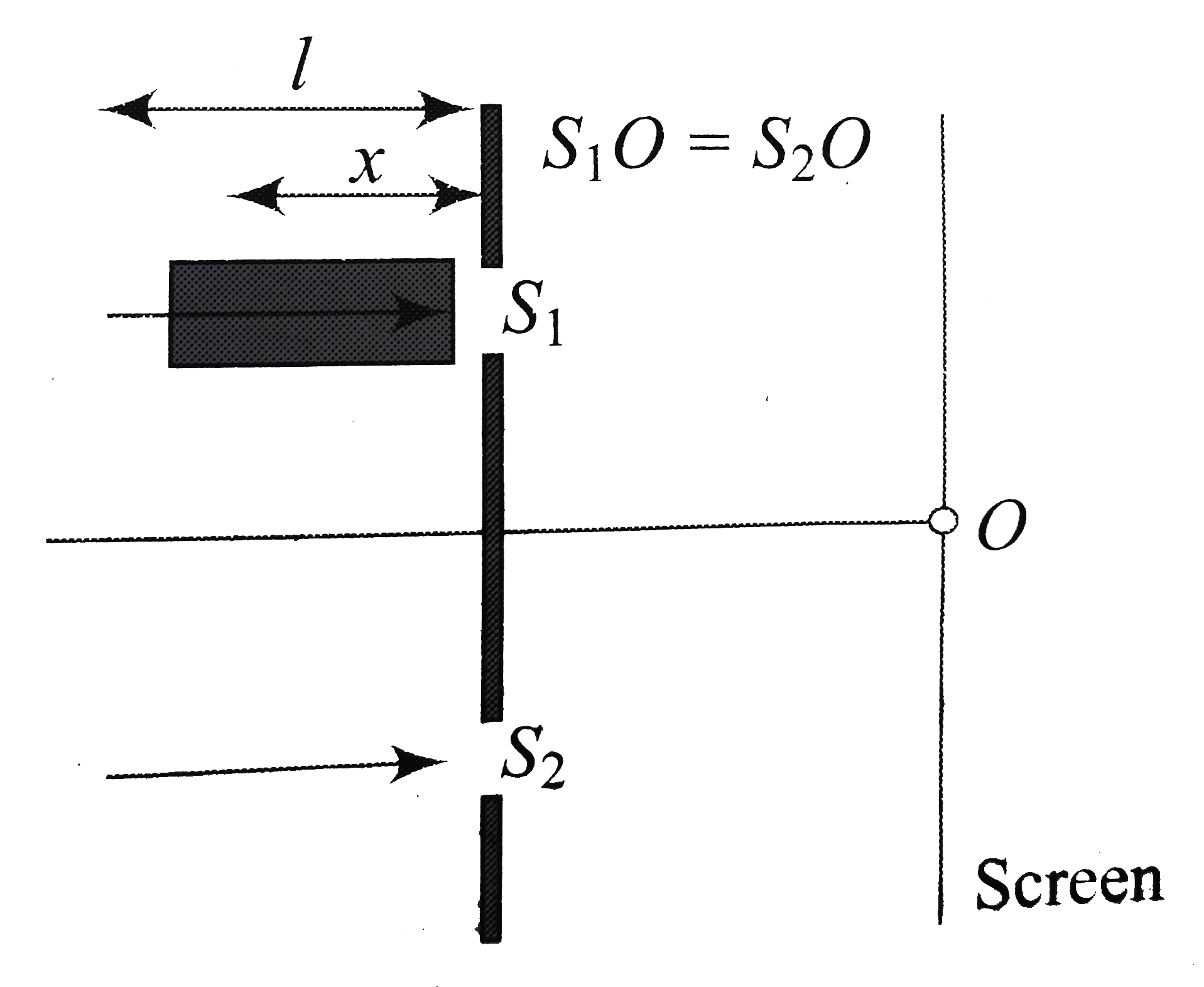B $\frac{λ}{l^{2}}$
C $\frac{l^{2}}{λ}$
Dnone of these
Question 3 - Select One
In Young’s double slit experiment, the distance between the two slits is made half, then the fringe width will become
AHalf
BDouble
COne fourth
DUnchanged

DC PANDEY-INTERFERENCE AND DIFFRACTION OF LIGHT-Level 2 More Than One Correct

Home
Ask Doubt
Profile