A convergent lens with a focal length of f=10cm is cut into two halves that are then moved apart to a distance of d=0.5 mm (a double lens). Find the fringe width on screen at a distance of 60 cm behind the lens if a point sources of monochromatic light (λ=5000Å) is placed in front of the lens at a distance of a = 15cm from it.
The correct Answer is:A
Applying lens formula , 1v−1u=1f
1v+115=110
∴V=30cm
m=vu=30−15=−2 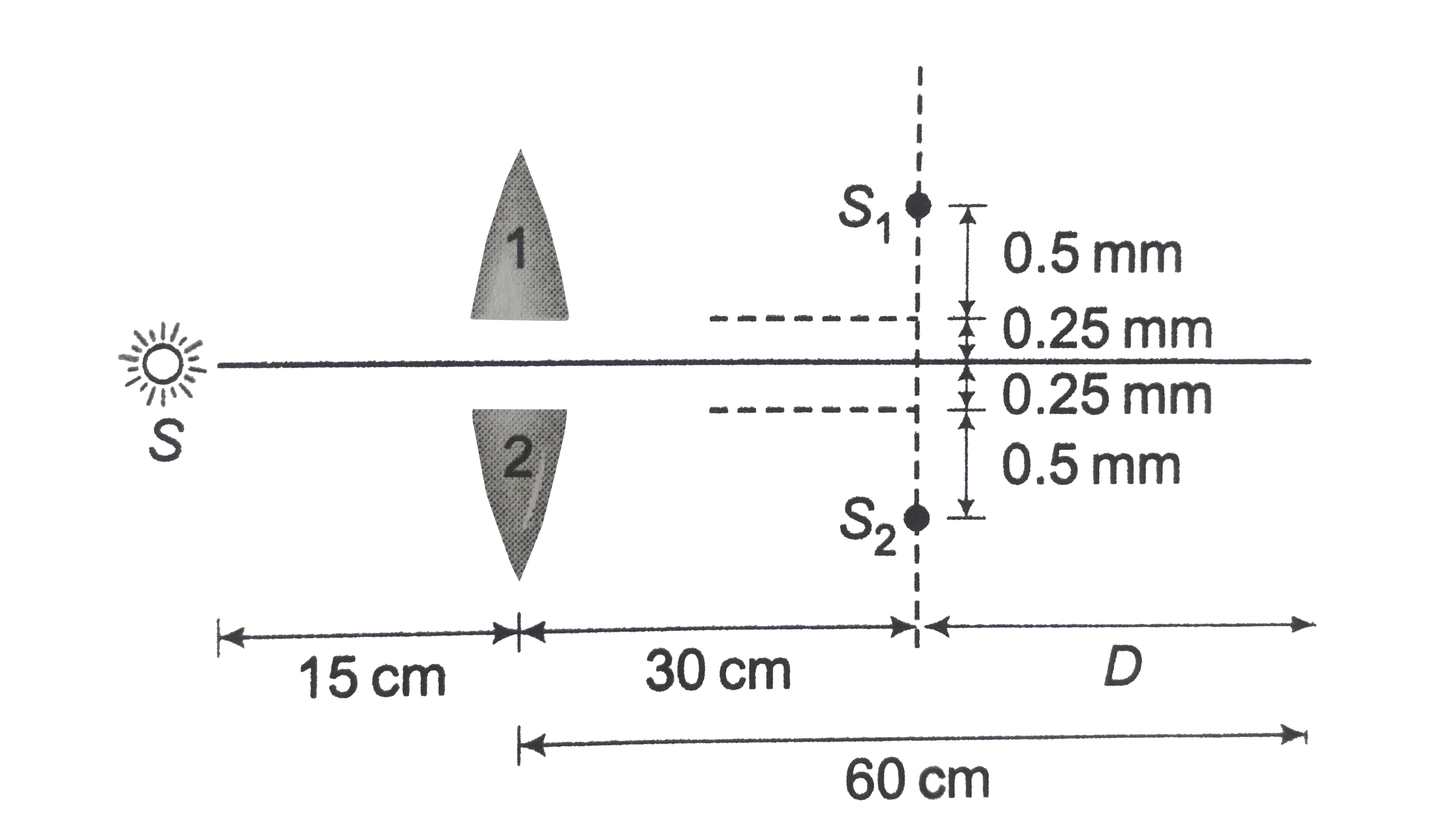
Distance between two slits,
d = 1.5 mm, D =30 cm
Fringe width, ω=λDd
=(5.0×10−7)(0.3)(1.5×10−3)=10−4m
=0.1 mm
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective
22 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
A convergent lens with a focal length of f = 10 cm is cut into two halves that are then moved apart to a distance of d =0.5 mm (a double lens). Find the fringe width on screen at a distance of 60 cm behind the lens if a pont source of monochromatic light (λ=5000Å) is placed in front of the lens at a distance of a = 15 cm from it.
View SolutionAn object is kept at a distance of 60 cm in front of a convex lens. Its real and inverted image is fonned at a distance of 20 cm from the lens. Find the focal length of the lens.
View Solution
Knowledge Check
A thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
A37.5 cmB16.25 cmC12.5 cmD13.5 cmA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
Avirtual and at a distance of 16 cm from the mirrorBreal and at a distance of 16 cm from the mirrorCvirtual and at a distance of 20 cm from the mirrorDreal and at a distance of 20 cm from the mirrorA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
AVirtual and at a distance of 16 cm from the mirrorBReal and at a distance of 16 cm from the mirrorCVirtual and at the distance of 20 cm from the mirrorDNone of the above
A convex lens of focal length 15 cm is split into two halves and the two halves are placed at a separation of 120 cm. Between the two halves of convex lens a plane mirror is placed horizontally and at a distance of 4 mm below the principal axis of the lens halves. An object AB of length 2 mm is placed at a distance of 20 cm from one half lens as shown in.figure. The final image of the point A is formed at a distance ofn3mm from the principle axis. Determine the value of n

View SolutionA lens with a focal length of 16cm produces a sharp image of an object in two positions, which are 60cm apart. Find the distance from the object to the screen.
View SolutionThe optical system consișt of a thin convex lens of focal length 30cmand a plane mirror 15cm behind the lens. An object is placed 15cm in front of the lens. The distance (in cm ) of final image from the lens is
View SolutionA thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
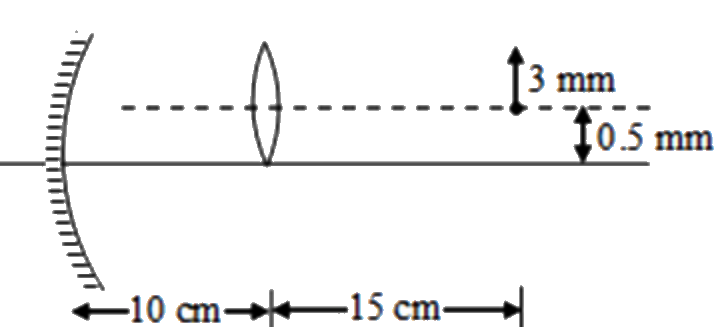
View Solution
