A candle of diameter d is floating on a liquid in a cylindrical container of diameter D(D<<d) as shown in figure. If is burning at the rate of 2cm/h then the top of the candle will :
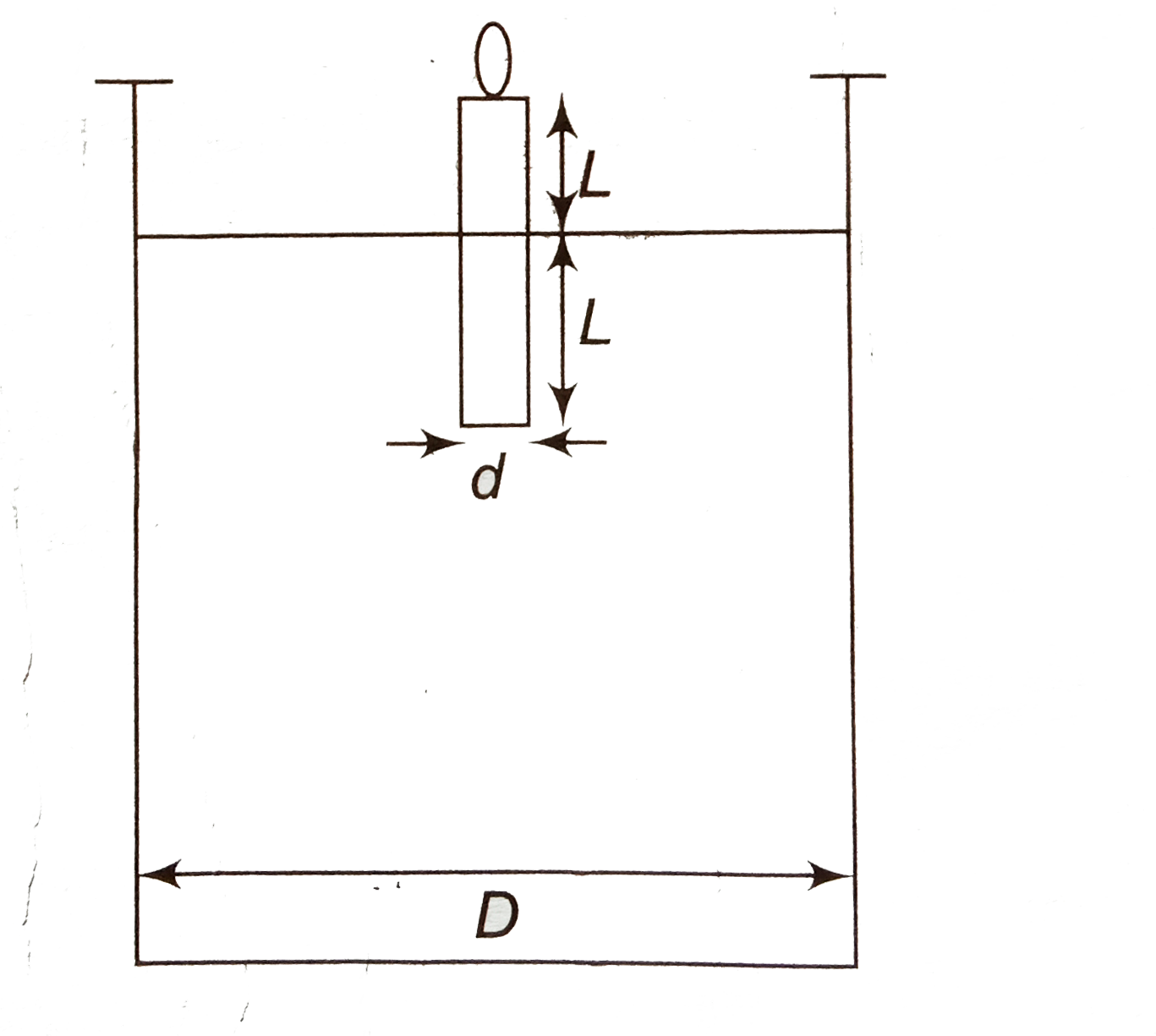
remain at the same height
fall at the rate of 1 cm/hour
fall at the rate of 2 cm/hour
go up at the rate of 1 cm/hour
The correct Answer is:B
Initial weight of the candle = weight of liquid displaced
ρCVCg=ρL (volume displaced) g
⇒ρCπ(d2)22L=ρLπd22Lg⇒ρCρL=12 ….(i)
When 2 cm has been burnt, total length =2L−2 But ρC(2L−2)=ρL(L−x)
ρC2(L−1)=2ρC(L−x) [Using eqn. (i)]
∴ x=1cm.
Outside also it has decreased 1 cm as the total decrease is 2 cm. The lelvel of the candle comes down at half
Topper's Solved these Questions
Similar Questions
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.
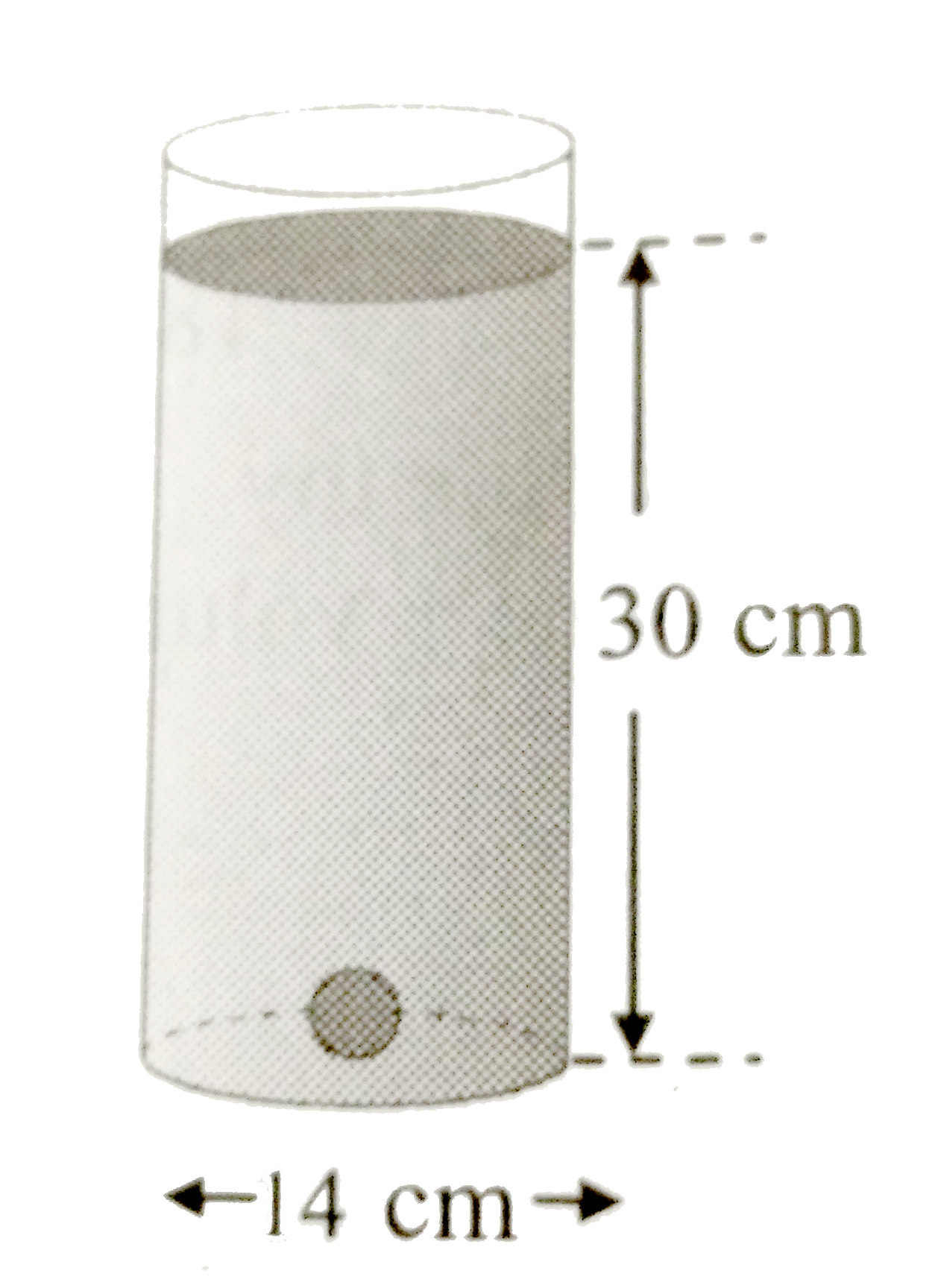 View Solution
View SolutionThe inner diameter ofa cylindrical container is 7 cm and its top is of the shape of a hemisphere, as shown in the figure. If the height of the container is 16 cm, find the actual capacity of the container.
View Solution
Knowledge Check
- Question 1 - Select One
A metallic sphere of diameter D has a cavity of diameter d at its centre. If the sphere is heated, the diameter of the cavity will:
ADecreaseBIncreaseCRemain unchangedDDecrease if d<D/2 and increase if d>D/2 - Question 2 - Select One
A beam of diameter 'd' is incident on a glass hemisphere as shown in the figure. If the radius of curvature of the hemisphere is very large in comparision to d, then the diameter of the beam at the base of the hemisphere will be:
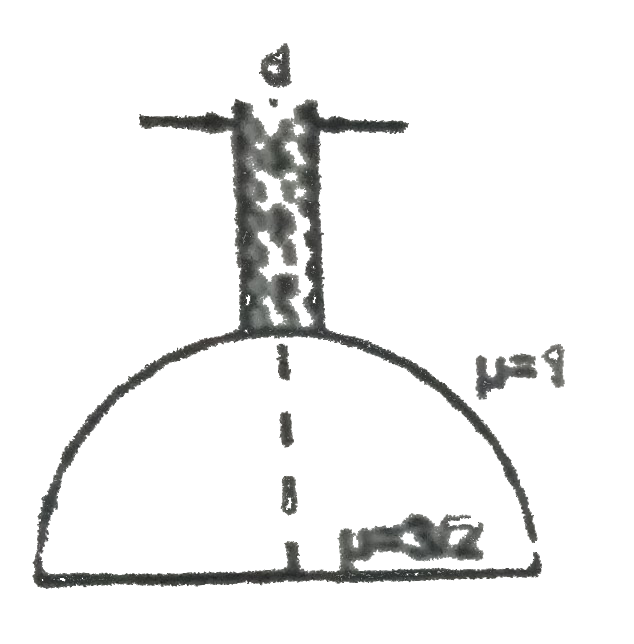 A34dBdCd3D23d
A34dBdCd3D23d - Question 3 - Select One
When a body of density d1 and volume V is floating in a liquid of density d2
Aits true weight is Vd2gBloss in its weight is Vd2gCits apparent weight is zeroDits density d1 is greater than that of liquid d2 .
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it . Find the volume of the water.
 View Solution
View SolutionAs shown in the figure, a cylindrical glass contains water with a metallic sphere of diameter 2 cm immersed in it. Find the volume of the water.
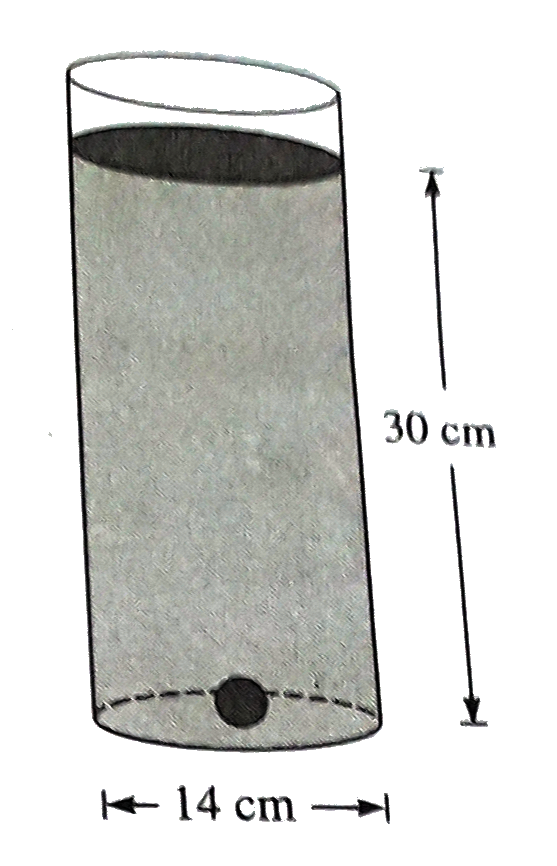 View Solution
View SolutionA hemispherical bowl of internal radius 12 cm contains liquid. This liquid is to be filled into cylindrical container of diameter 4 cm and height 3 cm. The number containers that is necessary to empty the bowl is (a) 80 (b) 96 (c) 100 (d) 112
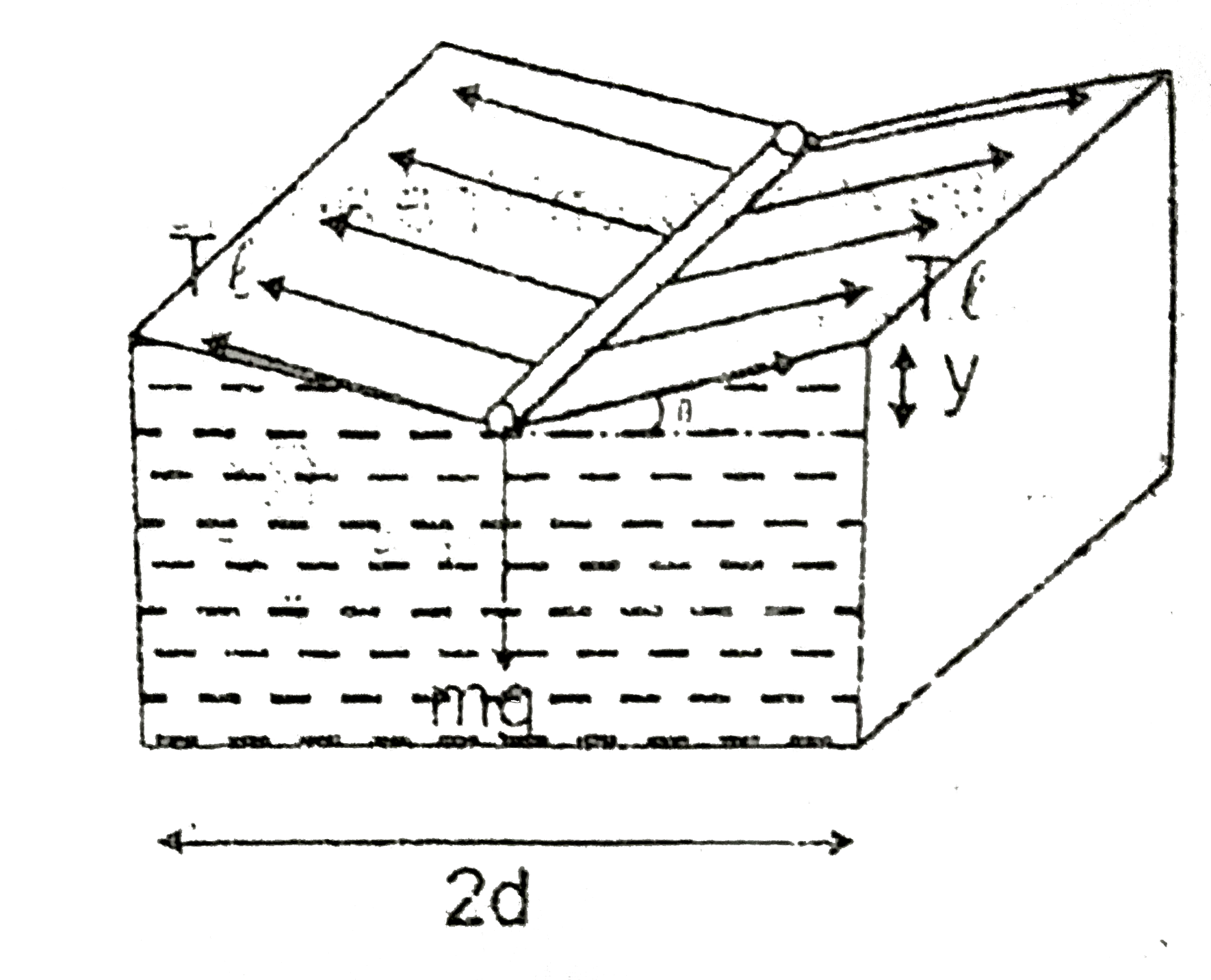
View SolutionA long thin straight uniform wire of negligible radius is supported on the surface of a liquid. The width of the container is 2d and the wire is kept at its centre, parallel to its length (as shown in figure). The surface of the liquid is depressed by a veritcal distance y(y<<d) at the centre as shown in figure. If the wire has mass λ per unit length, what is the surface tension of the liquid? igonre end effects.
 View Solution
View SolutionA drop of liquid of density p is floating half-immersed in a liquid of density d. If σ is the surface tension, then the diameter of the drop of the liquid is
View Solution

