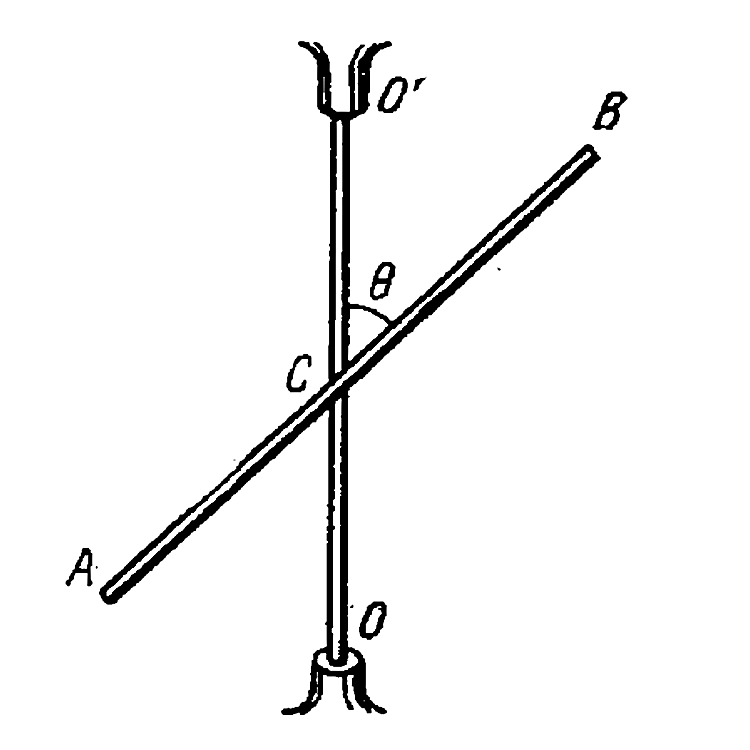
A given shaped glass tube having uniform cross-section is filled with water and is mounted on a rotatable shaft as shown in figure. If the tube is rotated with a constant angular velocity ω then :

water levels in both sections A and B go up
water level in section A goes up and that in B comes down
water level in section A comes down and that in B it goes up
water levels remain same in both sections
The correct Answer is:A
Due to rotation about the axis OO', a force is acting on the luqiid column AB outwards, pushing up the liquid column on the right. This centrifugal force acting on the right. This centrifugal force acting on the small element dx f area of cross- section dx, distant x from the axis is dmω2x=Adxρω2x
The total force due to column of length L(=AB) is
LA0ρω2⋅xdx=Aρω2L22
Pressure at B= atmospheric pressure +h1ρg+Aρω2AL22
Pressure at B due to liquid column on the right hand side = atmospheric pressure +h2ρg
Net pressure due to the left hand side = pressure at B due to liquid column
atm, pressure +h1ρg+ρω2L22= atm. pressure +h2ρg
∴ h2−h1=H0=ω2L22g
Here one has

H2=ω2t222g,H1=ω2L212g
As ω is the same, and L2>L1,H2>H1. But Both will go up.

Topper's Solved these Questions
Similar Questions
A midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.
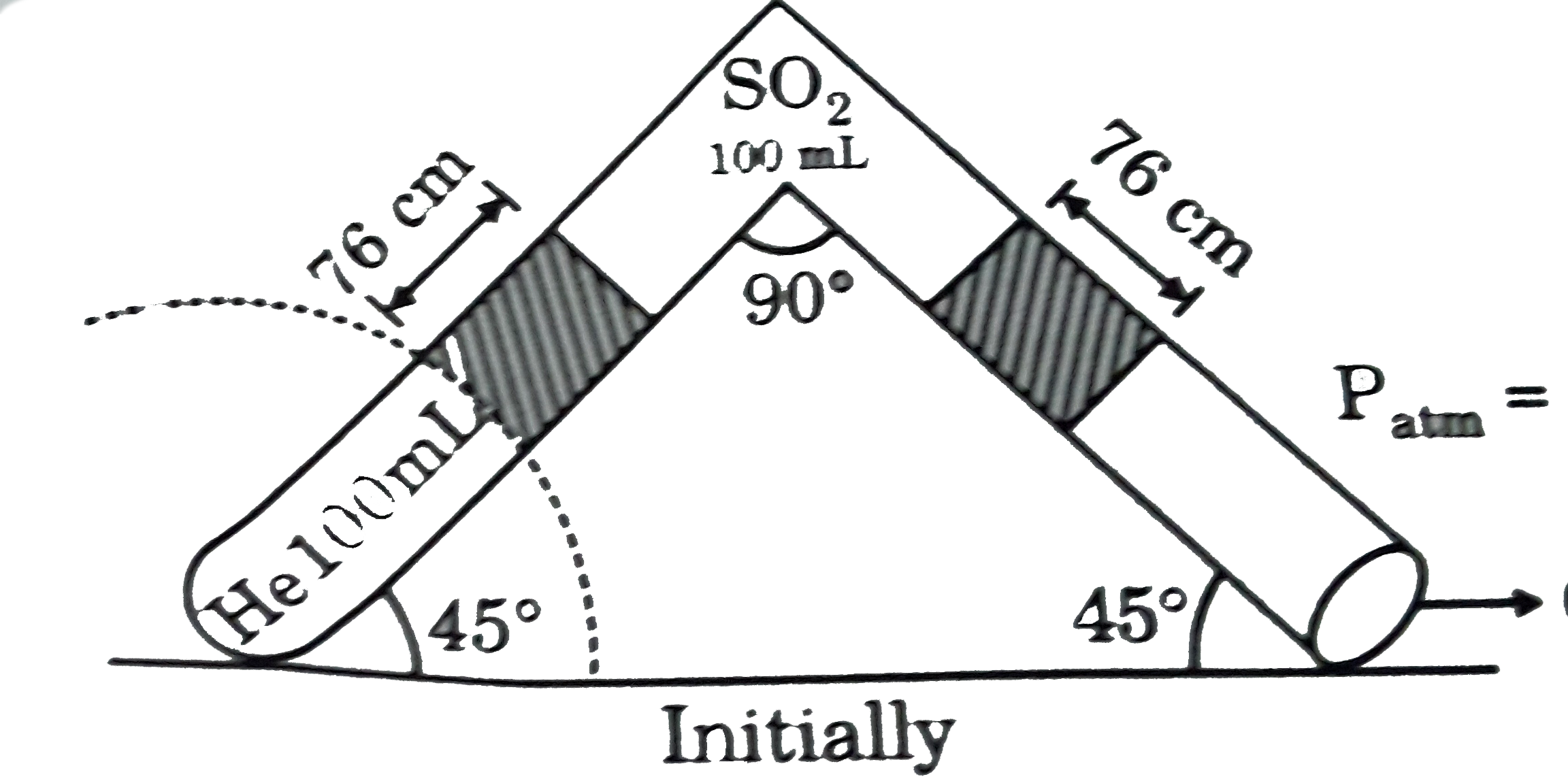
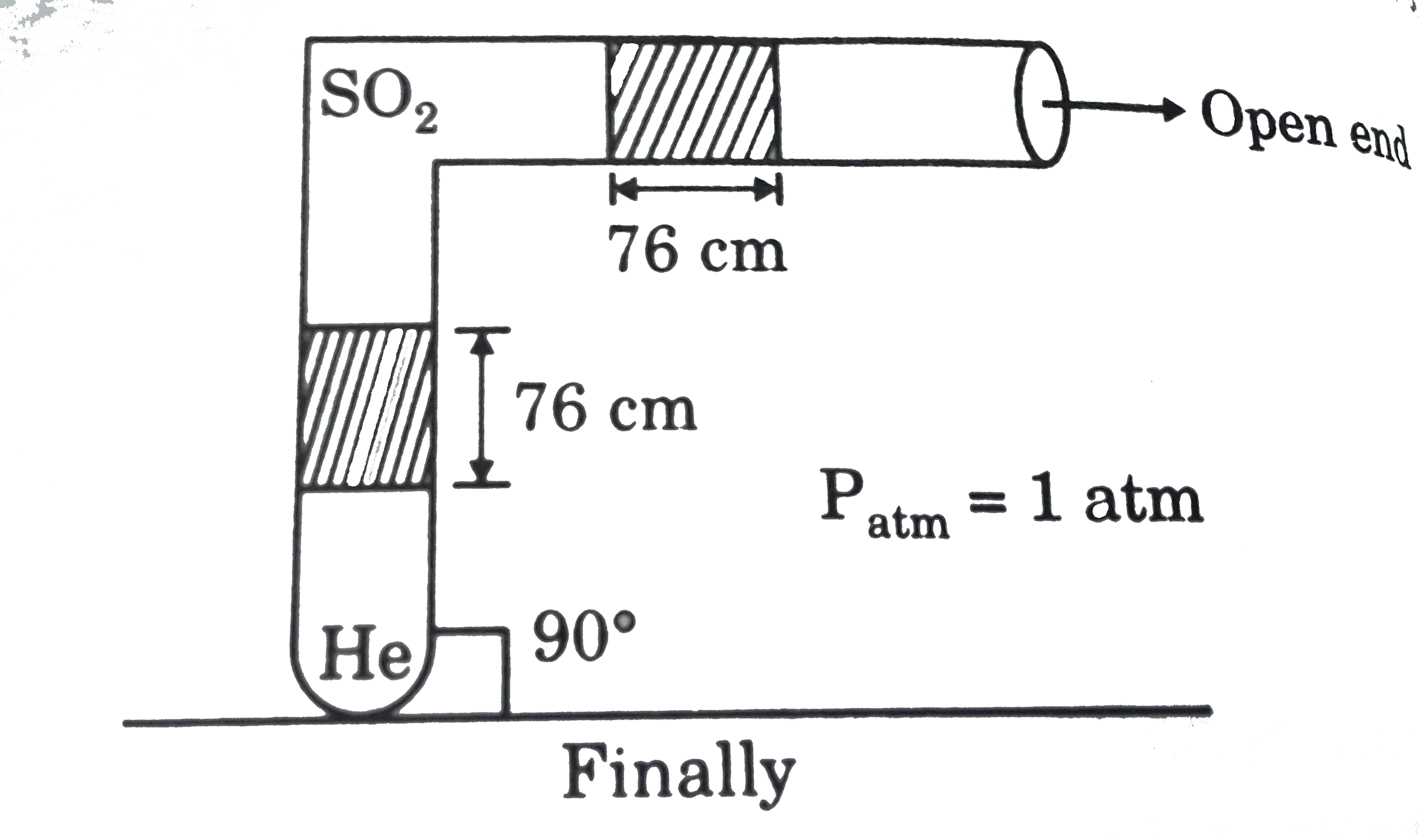
View SolutionA thin glass tube (uniform cross-section) is filled with He and SO2 in between Hg column as shown in diagram. When it is rotated by angle 45∘ anticlockwise as shown in diagram, calculate the sum of final volume of both gases (Assume T remains constant) [Use : 1√2=0.7]
View Solution
Knowledge Check
In the above problem, if the coil rotates with a constant angular velocity ω, the emf induced in it
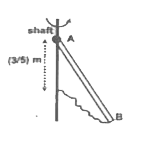
A(a) is zeroB(b) changes non-linearly with timeC(c ) has a constant value =BanωD(d ) has a maximum value =BanωA rod AB of length l = 1m and mass m = 2kg is pinned to a vertical shaft and a massless string is tied with the shaft at the lower end of the rod ( length of the string is 45m ) as shown in figure.If the shaft starts rotating with a constant angular velocity ω=5 rad / sec. Then find the tension in the string.
 A1NB2NC3ND0N
A1NB2NC3ND0NA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.
 Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of these
Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of these
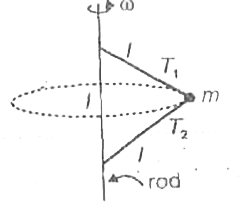
In the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA rotating disc moves in the positive direction of x-axis as shown. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre C of the disc was located at origin after which
a. it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity ω. b. it moved with constant velocity v while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).
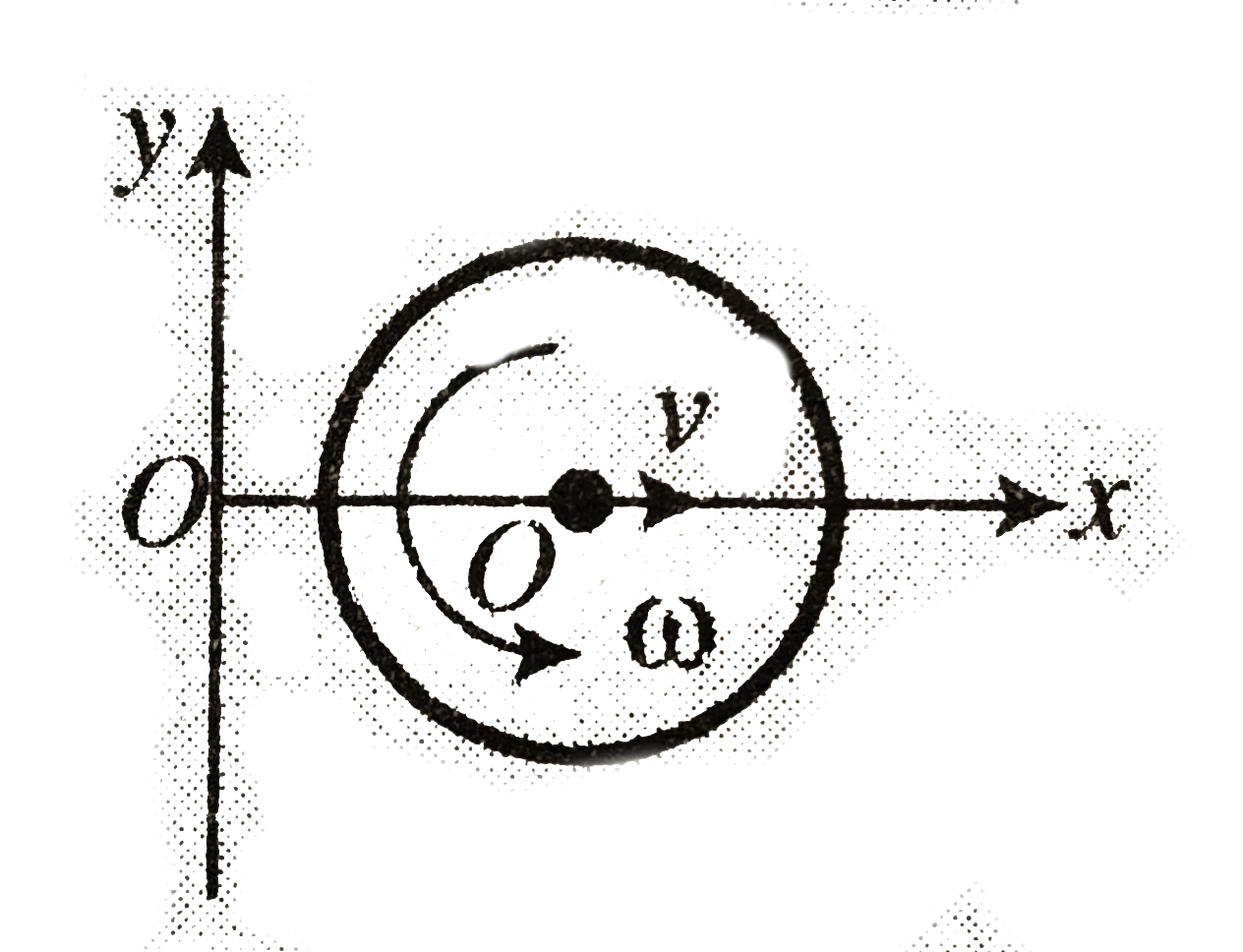
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
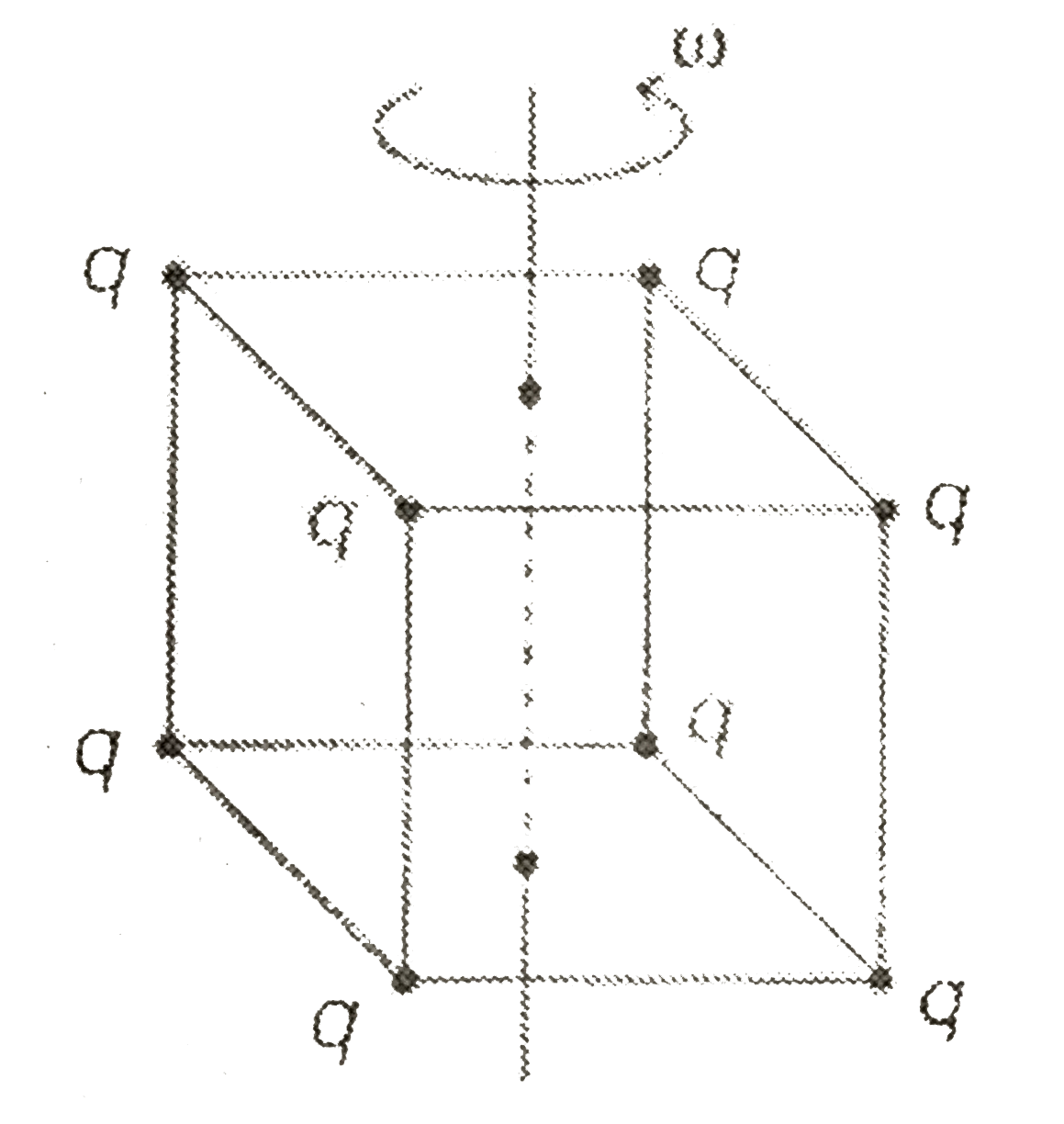
View SolutionConsider a cube of side 'a' as shown. Eight point charges are placed at the corners. The cube is rotated about the centroidal axis with constant angular velocity ω :
View SolutionA coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
View Solution
