Assertion : When a sphere is rolls on a horizontal table it slows down and eventually stops.
Reason : When the sphere rolls on the table, both the sphere and the surface deform near the contact. As a result, the normal force does not pass through the centre and provide an angular declaration.
Assertion is correct, reason is correct, reason is a correct explanation for assertion.
Assertion is correct, reason is correct, reason is not a correct explanation for assertion
Assertion is correct, reason is incorrect
Assertion is incorrect, reason is correct
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
A sphere is rolled on a rough horizontal surface. It gradually slows down and stops. The force of friction tries to
Adecrease the angular velocity of the sphereBincrease the angular velocity of the sphereCdecrease the linear velocity of the sphereDincrease the linear momentum of the sphereAssertion: When a sphere of perfectly hard material is rolled on a perfectly hard surface then sphere never stops.
Reason: Friction becomes zero at the contactAIf both assertion and reason are correct and reason is the correct explanation of the assertion.BIf both assertion and reason are correct but reason is not the correct explanation of assertion.CIf assertion is correct but reason is incorrect.DIf assertion is incorrect but reason is correct.When a sphere rolls down an inclined plane, then identity the correct statement related to the work done by friction force.
Athe friction force does positive translational workBthe friction force does negative rotational workCThe net work done by friction is zeroDall of the above
When a sphere rolls down an inclined plane, then identity the correct statement related to the work done by friction force.
View SolutionA solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be 7nmvR/. Find the value of n
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then :
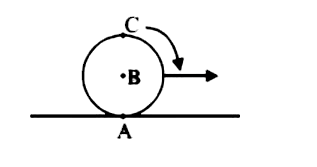
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact. B is the centre of the sphere and C is its topmost point. Then
 .
.
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
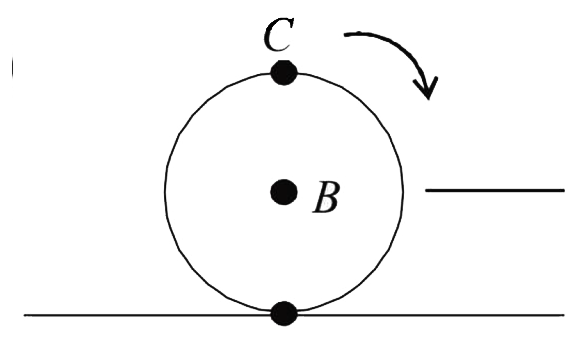
View Solution
