A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then :
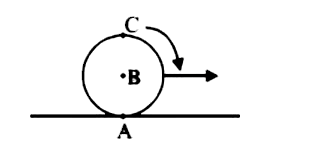
→VC−→VA=2(→VB−→VC)
→VC−→VB=→VB−→VA
∣∣→VC−→VA∣∣=2∣∣→VB−→VC∣∣
∣∣→VC−→VA∣∣=4∣∣→VB∣∣
The correct Answer is:C
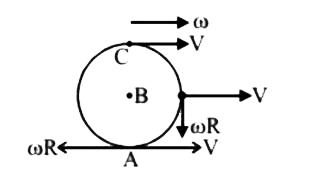
→VA=Vˆi+ωR(−ˆi),→VB=Vˆi,→VC=Vˆi+ωRˆi
→VC−→VA=2ωRˆi
2[→VA−→VC]=2[V(i)−V(i)−ωR(i)]=−2ωR(i)
Hence →VC−→VA=−2(→VB−→VC)
Topper's Solved these Questions
Similar Questions
Knowledge Check
When a hollow sphere is rolling without slipping on a rough horizontal surface then the percentage of its total K.E. which is translational is
A72%B28%C60%D40%A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative
 AThe acceleration of the centre of the sphere is 9.8m/s2BThe acceleration of the centre of the sphere is 10m/s2CThe direction of frictional force on the sphere is towards rightDThe value of frictional force is 3N
AThe acceleration of the centre of the sphere is 9.8m/s2BThe acceleration of the centre of the sphere is 10m/s2CThe direction of frictional force on the sphere is towards rightDThe value of frictional force is 3NAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.AAssertion is True, Reason is True, Reason is a correct explanation for AssertionBAssertion is True, Reason is True, Reason is not a correct explanation for AssertionCAssertion is False but, Reason is True.DAssertion is True, Reason is False
A uniform sphere of radius R has a spherical cavity of radius R2 (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find:
(a) The kinetic energy of the sphere at this moment.
(b) The velocity of the centre of mass at this moment.
(c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing

View SolutionA disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
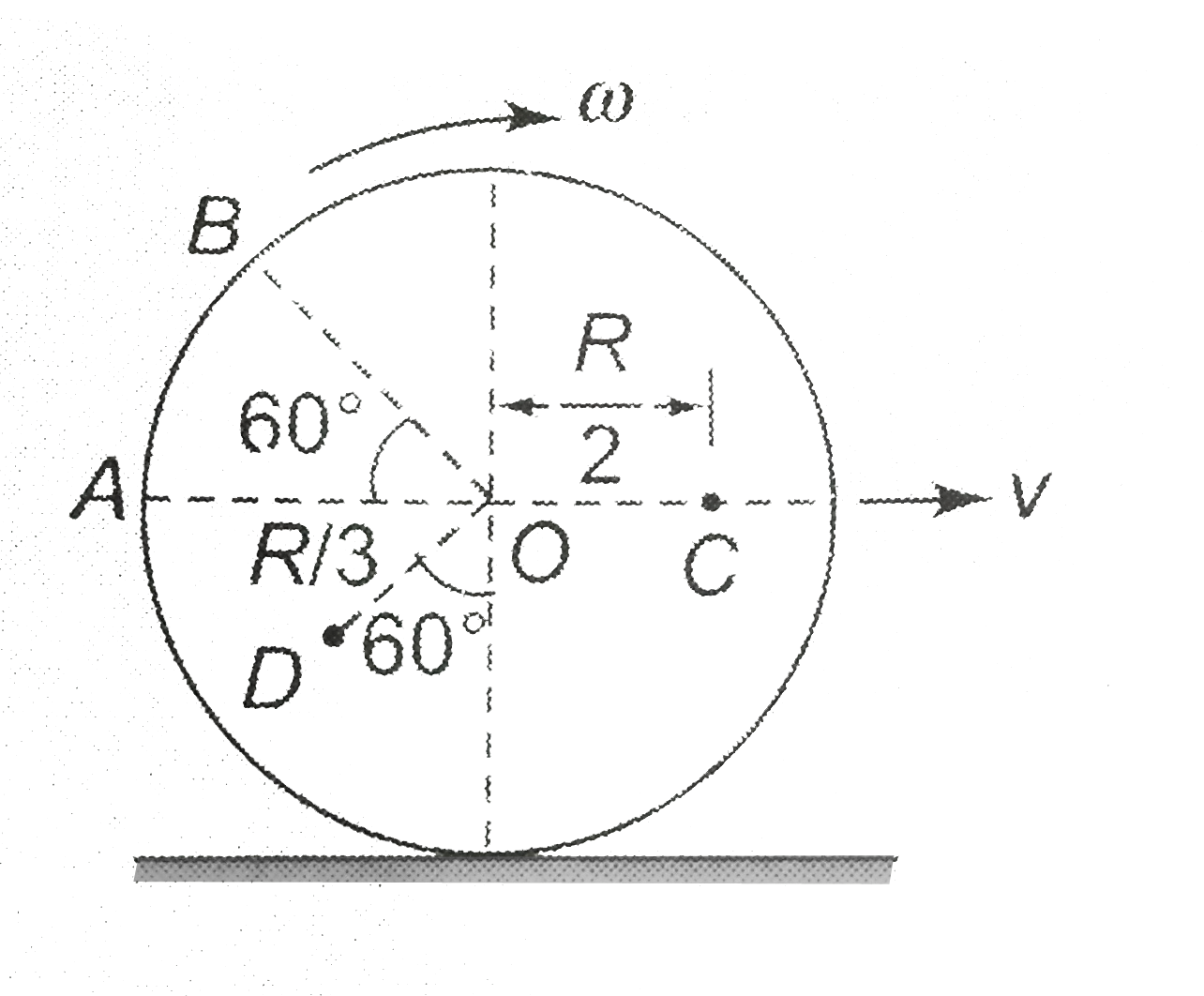
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View SolutionA solid sphere rolls without slipping along a horizontal surface. What percentage of its total kinetic energy is rotational kinetic energy?
View Solution
