Two rods of the same length L but cross-section in the ratio SB/SA=4 are joined at a heater H and a heat sink S as shown. The rate of heat flow to s is found to be Ro If points of A and B at distance L/3 each from H are now joined by a conductor C of length L and the cross-section of C is such that 3c=2S/A, the new rate of heat flow to S will be (See figure)

65Ro
1312Ro
Ro
75Ro
The correct Answer is:C
The fall of temperature from H to A is the same as the fail of temperature from H to B. Hence on joining A and B by the conductor. No heat transfer will take place through the conductor .
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
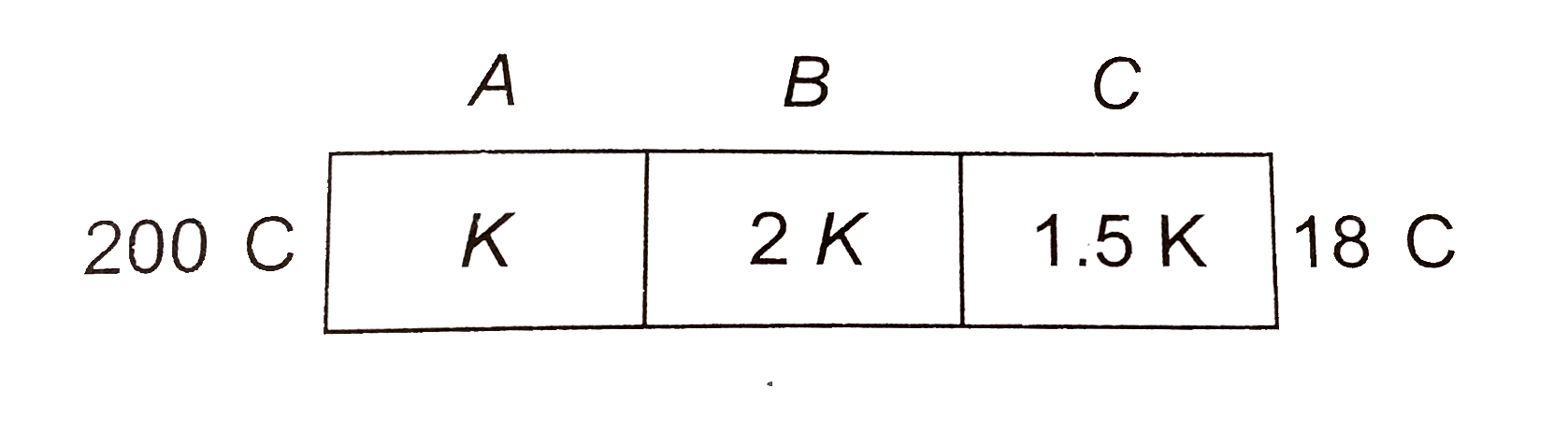 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘CA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
Ai2lρπr2Bi2(lρπr2)2Ci2lρ/rDilρ/r
Resistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionThree rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.

View SolutionThree rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.

View Solution
