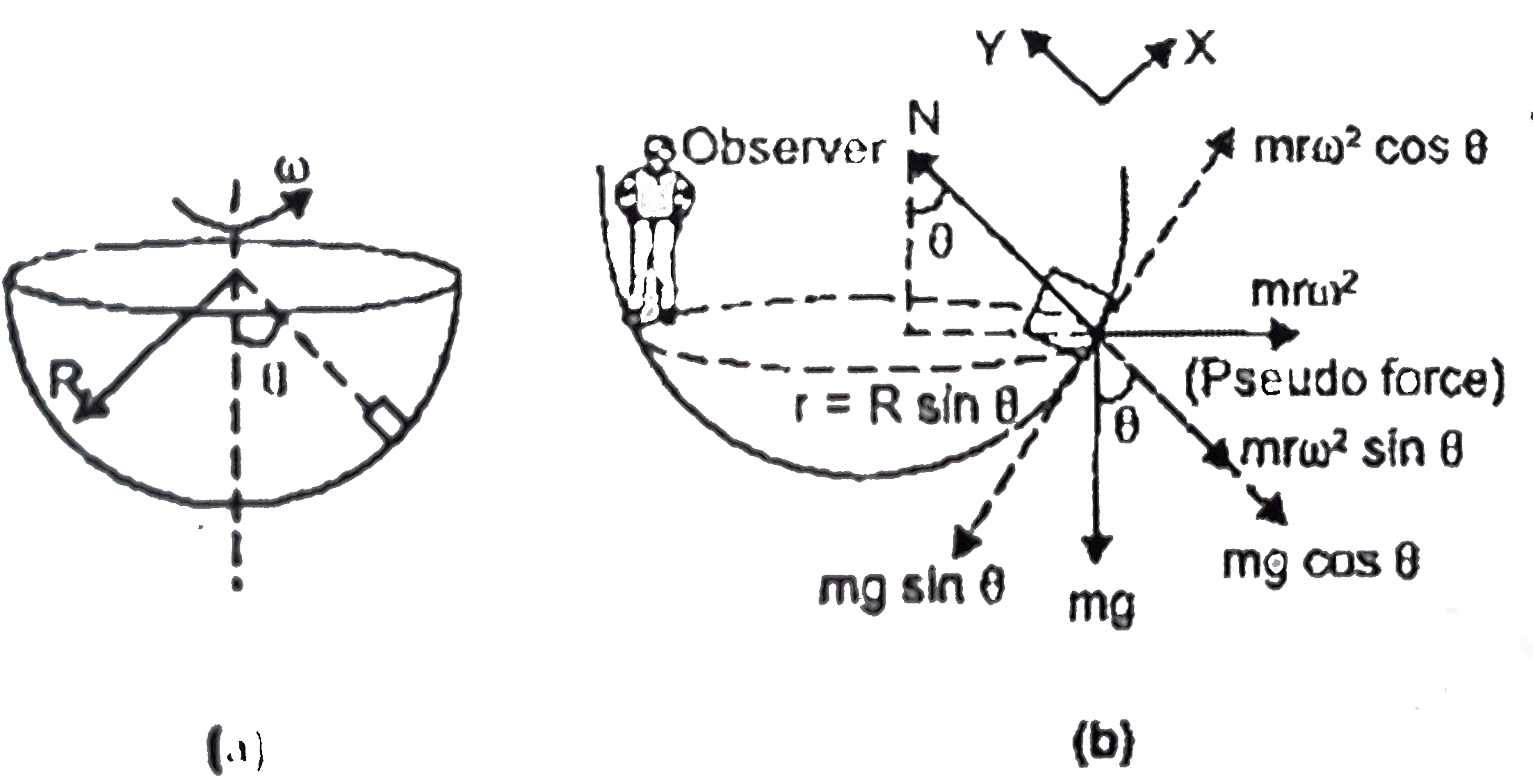
A spherical bowl of radius R rotates about the verical diameter with angular velocity .The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle with the vertical (see figure). Then

The correct Answer is:A
Reaction N has component in vertical direction equal to the weight of the object . The horizontal component of N provides the centripetal force. Now { can be calculated }
Topper's Solved these Questions
Similar Questions
A spherical bowl of radius R rotates about the vertical diameter. The bowl contains a samll object whose radius vector in the course of rotation makes an angle α with the vertical (Fig.). What should be the minimum angular velocity ω of the bowl in order to prevent the object from sliding down, if the coefficient of static friction is μstat?

View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png) Ag√3B2g√3rC√3grDgr
Ag√3B2g√3rC√3grDgr
A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View Solution
