Question

A spherical bowl of radius R rotates about the vertical diameter. The bowl contains a samll object whose radius vector in the course of rotation makes an angle $\alpha$ with the vertical (Fig.). What should be the minimum angular velocity $\omega$ of the bowl in order to prevent the object from sliding down, if the coefficient of static friction is ${\mu }^{\text{stat}}$?

Answer

`sqrt((g tan (alpha-varphi))/(R sin alpha)) le omega le sqrt((g tan (alpha+varphi))/(R sin alpha))`, where `varphi="arc tan"mu`

Explanation

Since the object is at rest, the direction of the force of friction is not known. For this reason we shall imagine the angular velocity to be decreased until the object starts sliding downwards. The force of friction will then be directed as shown in Fig. The equations of motion are of the form
`N sin alpha - T cos alpha - m omega^(2)R sin alpha`
`N Cos alpha | T sin alpha - mg = 0`
where `T= mu^("stat")= tan varphi` we obtain after some simple transformations
`omega_(1)= sqrt((g tan (alpha-varphi))/(R sin alpha))`
Suppose we imagine the angular velocity to be increased, so that the object starts sliding upwards. Then the direction of the force of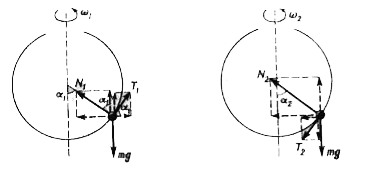
friction will change sign (Fig.) and the equations of motion will assume the form
`N sin alpha + T cos alpha = m omega^(2) R sin alpha`
`N cos alpha - T sin alpha - mg = 0`
`T = mu^("stat")N = N tan varphi`
from which we get
`omega_(2) = sqrt((g tan (alpha+varphi))/(R sin alpha))`
Thus the body will be in equilibrium if
`sqrt((g tan (alpha-varphi))/(R sin alpha)) le omega le sqrt((g tan (alpha+varphi))/(R sin alpha)) `
Obviously, if `alpha le varphi`, i.e. if `tan alpha le mu^("stat")`, the object will not slide down, even when the bowl stops rotating.
As a particular case of the solution when static friction is absent `(mu^("stat")=tan varphi = 0)` equilibrium will be established when the bowl rotates at an angular velocity of
`omega_(0)= sqrt(g//R cos alpha)`