A disc of radius 20 cm and mass half kg is rolling on an inclined plane. Find out frictio force so that disc performs pure rolling.

A

$\frac{5 \sqrt{2}}{3} N$

B

$\frac{5}{3 \sqrt{2}} N$

C

$\frac{5}{\sqrt{2}} N$

D

$\frac{5}{2 \sqrt{3}} N$

Text Solution

Verified by Experts

The correct Answer is:B

$M g sin θ - f = m a_{c m}$ . . . (i)
$f_{R} = \frac{M R^{2}}{2} (\frac{a_{m c}}{R})$
$f = \frac{M a_{c m}}{2}$
or $a_{c m} = \frac{2 f}{M}$
so $m g sin θ - f = M (\frac{2 f}{M})$
$f = \frac{m g sin θ}{3}$
$f = \frac{1}{2} \times \frac{10}{3} \times \frac{1}{\sqrt{2}} = \frac{5}{3 \sqrt{2}}$ newton

|

Updated on:21/07/2023

Class 12 PHYSICS AIIMS 2019 25 MAY MORNING SHIFT

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A $\frac{7}{6}$
B $\frac{5}{4}$
C $\frac{3}{2}$
Ddepends on angle of inclination
Question 2 - Select One
A disc of radius R is rolling down an inclined plane whose angle of inclination is $θ$ Its acceleration would be
A $\frac{5}{7} g sin θ$
B $\frac{2}{3} g sin θ$
C $\frac{1}{2} g sin θ$
D $\frac{3}{5} g sin θ$
Question 3 - Select One
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)

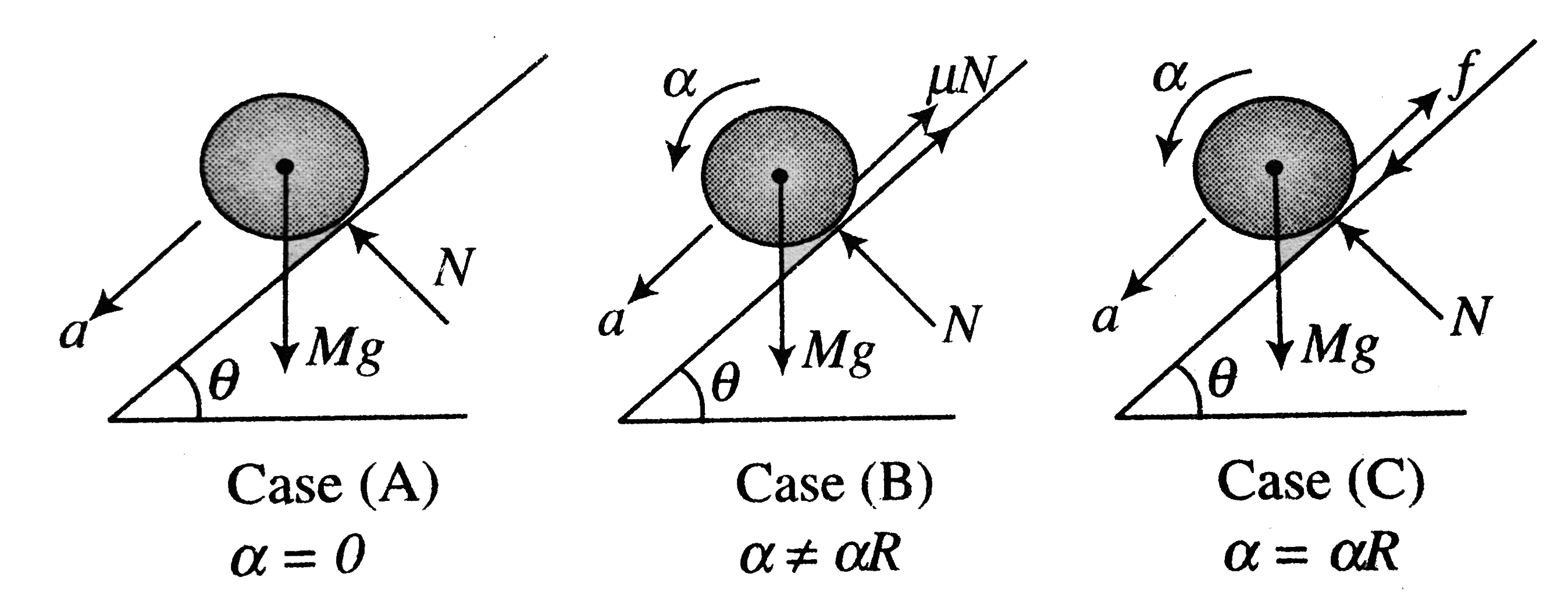
We have four objects: a solid sphere, a hollow sphere, a ring and a disc, all of same radius. When these are released on an inclined plane, it may happen that all of them do not perform pure rolling. But from the information of pure rolling, if one object can be confirmed to be purely rolling then it can be said that rest all will perform pure rolling. This object whose pure rolling confirms pure rolling of all other objects is
Ahollow sphere
Bsolid sphere
Cring
Ddisc

AIIMS PREVIOUS YEAR PAPERS-AIIMS 2019 25 MAY MORNING SHIFT-PHYSICS

Home
Ask Doubt
Profile