In maxwell's speed distribution curve, for N2 gas, the average of |relative velocity| between two molecules at 300 k will be : -
300 m/sec
610 m/sec
920 m/sec
zero
The correct Answer is:B
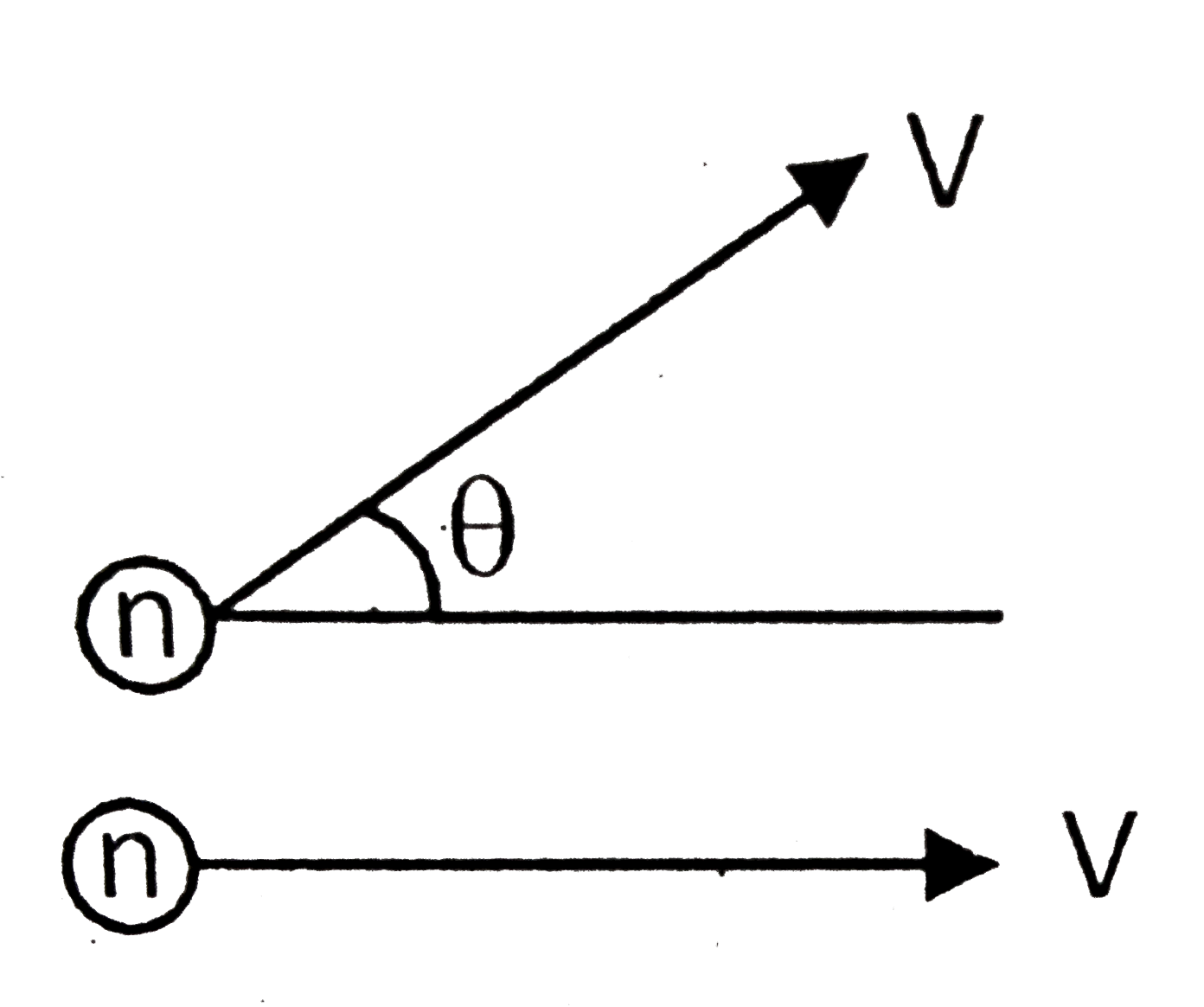
|Vrel|=√V2+V2−2(V)(V)cosθ=2V∣∣∣sinθ2∣∣∣
⟨Vrel⟩=π∫02V1∣∣sinθ2∣∣dθπ∫0dθ=4Vπ
⟨Vrel⟩=4πVaverage=4π√8RTπm0=4π√8×8.3×3003.14×28×10−3=606 m/sec
Topper's Solved these Questions
Similar Questions
Knowledge Check
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
AvB(π/4)vC(4/π)vDZeroStatement-1 : Rotational KE of a gas molecule follows Maxwell's speed distribution curve.
Statement-2: Rotational KE & translational KE of a diatomic gas molecule is same,A1-true 2-falseB1-false 2-trueC1-false 2-falseD1-true 2-falseWhat is the average velocity of H2 molecules at 100K relative to their velocity at 50K?
A2.00 times the velocity at 50KB1.41 times the velocity at 50KC0.71 times the velocity at 50KD0.50 times the velocity at 50K
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
View SolutionMaxwell’s Speed Distribution Curve||Collision Frequency || Mean free Path
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
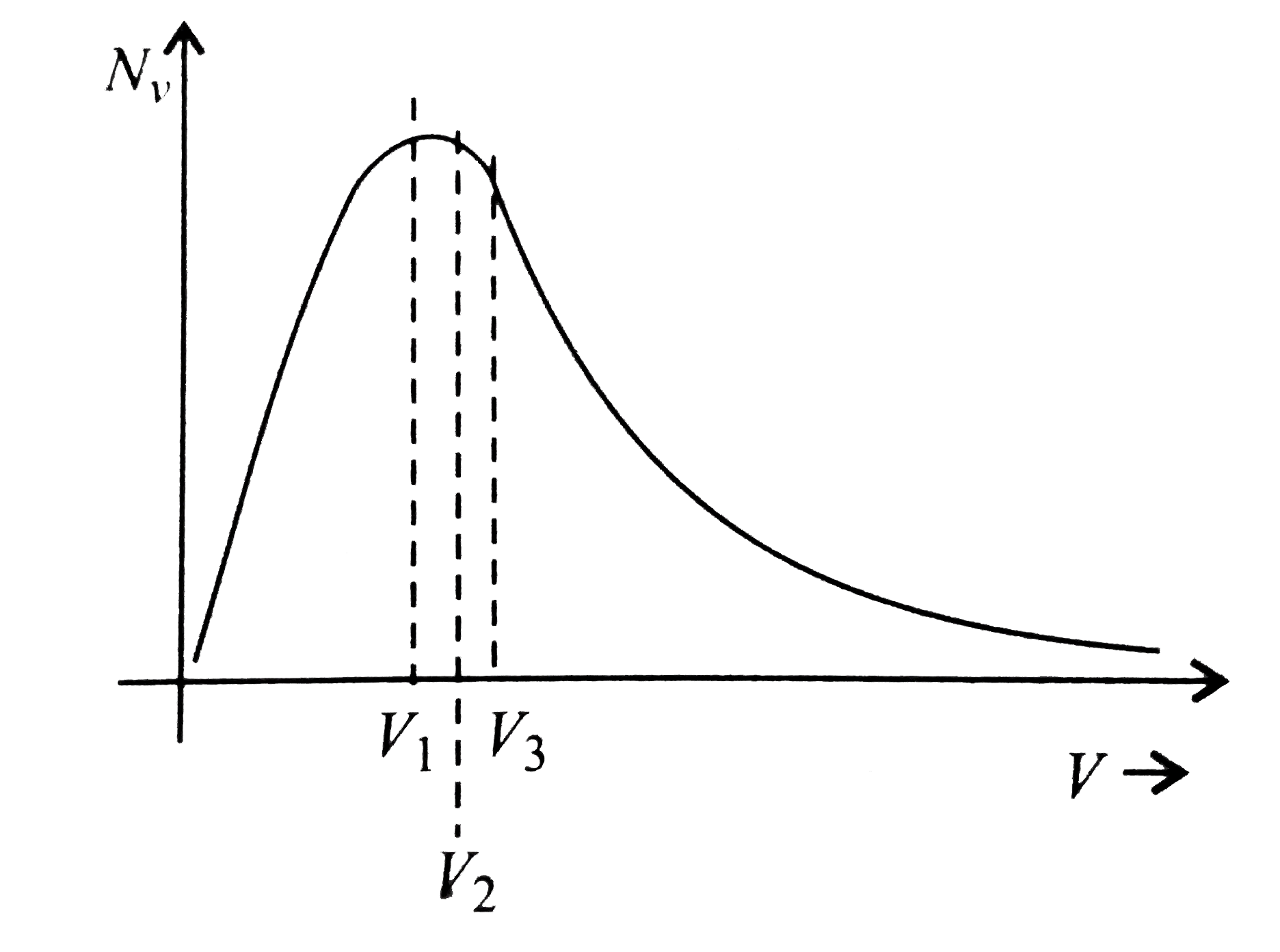
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr where
View Solution
