A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
v
(π/4)v
(4/π)v
Zero
The correct Answer is:C
To find the average relative velocity between any two particles moving with speed v and having randomly distributed directions, we can follow these steps:
Step 1: Understand Relative Velocity
The relative velocity vr between two particles can be expressed as:
vr=v1−v2
where v1 and v2 are the velocities of the two particles.
Step 2: Magnitude of Relative Velocity
If both particles have the same speed v and the angle between their directions is θ, the magnitude of the relative velocity can be calculated using the formula:
|vr|=|v1−v2|=√v2+v2−2v2cosθ
This simplifies to:
|vr|=√2v2(1−cosθ)=v√2(1−cosθ)
Step 3: Use Trigonometric Identity
Using the trigonometric identity 1−cosθ=2sin2(θ/2), we can rewrite the expression for the magnitude of the relative velocity:
|vr|=v√2⋅2sin2(θ/2)=2vsin(θ/2)
Step 4: Average Over All Angles
To find the average relative velocity, we need to average this expression over all possible angles θ from 0 to 2π:
⟨|vr|⟩=12π∫2π02vsin(θ/2)dθ
Step 5: Change of Variable
Let u=θ/2, then dθ=2du and the limits change from 0 to π:
⟨|vr|⟩=12π∫π04vsin(u)du
Step 6: Evaluate the Integral
The integral of sin(u) is:
∫sin(u)du=−cos(u)
Thus,
∫π0sin(u)du=(−cos(u))π0=−cos(π)−(−cos(0))=1+1=2
Step 7: Final Calculation
Substituting back into our average expression:
⟨|vr|⟩=12π⋅4v⋅2=4vπ
Conclusion
The average relative velocity between any two particles is:
⟨|vr|⟩=4vπ
The relative velocity vr between two particles can be expressed as:
vr=v1−v2
where v1 and v2 are the velocities of the two particles.
If both particles have the same speed v and the angle between their directions is θ, the magnitude of the relative velocity can be calculated using the formula:
|vr|=|v1−v2|=√v2+v2−2v2cosθ
This simplifies to:
|vr|=√2v2(1−cosθ)=v√2(1−cosθ)
Using the trigonometric identity 1−cosθ=2sin2(θ/2), we can rewrite the expression for the magnitude of the relative velocity:
|vr|=v√2⋅2sin2(θ/2)=2vsin(θ/2)
To find the average relative velocity, we need to average this expression over all possible angles θ from 0 to 2π:
⟨|vr|⟩=12π∫2π02vsin(θ/2)dθ
Let u=θ/2, then dθ=2du and the limits change from 0 to π:
⟨|vr|⟩=12π∫π04vsin(u)du
The integral of sin(u) is:
∫sin(u)du=−cos(u)
Thus,
∫π0sin(u)du=(−cos(u))π0=−cos(π)−(−cos(0))=1+1=2
Substituting back into our average expression:
⟨|vr|⟩=12π⋅4v⋅2=4vπ
The average relative velocity between any two particles is:
⟨|vr|⟩=4vπ
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-01
Explore 55 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-02
Explore 57 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionIn maxwell's speed distribution curve, for N2 gas, the average of |relative velocity| between two molecules at 300 k will be : -
View SolutionA particle is moving with speed v in a circle of radius R. Find the magnitude for average velocity of point
for the half revolution
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionThe magnitude of average velocity is equal to the average speed when a particle moves:-
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in the Fig. The distance traversed by the particle between (a) t=0s→10s .
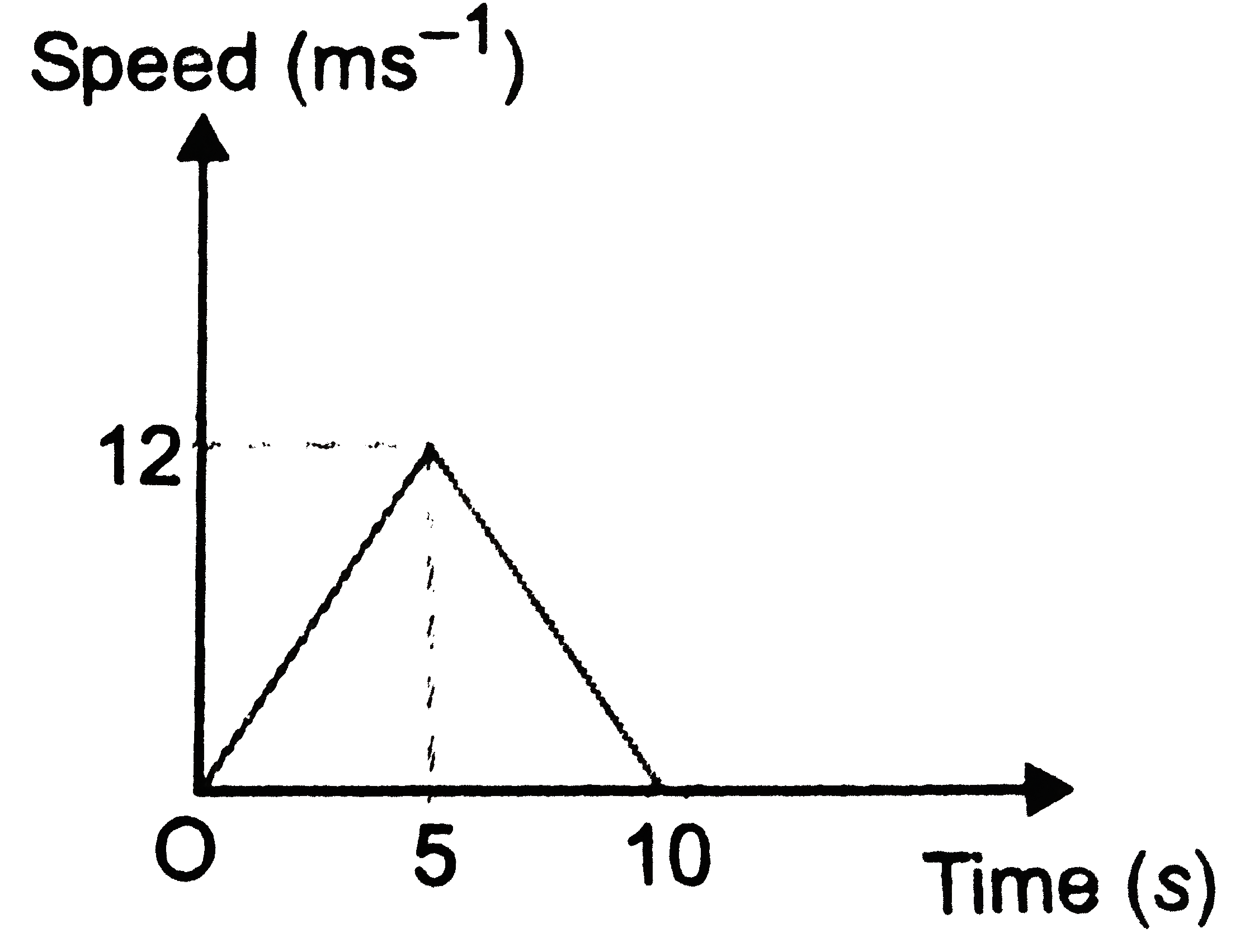 .
what is the average speed of the particle over the intervals?
.
what is the average speed of the particle over the intervals?
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionA particle travels two and a half revolutions of the circle of radius R in time t. The ratio of the average speed of the particle to the magnitude of the average velocity in this time interval is
View SolutionThe velocity and time graph for a particle moving in a straight line s shown in the figure. Then, the average velocity between t=4 s and t=6 s is _____

View SolutionThe fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
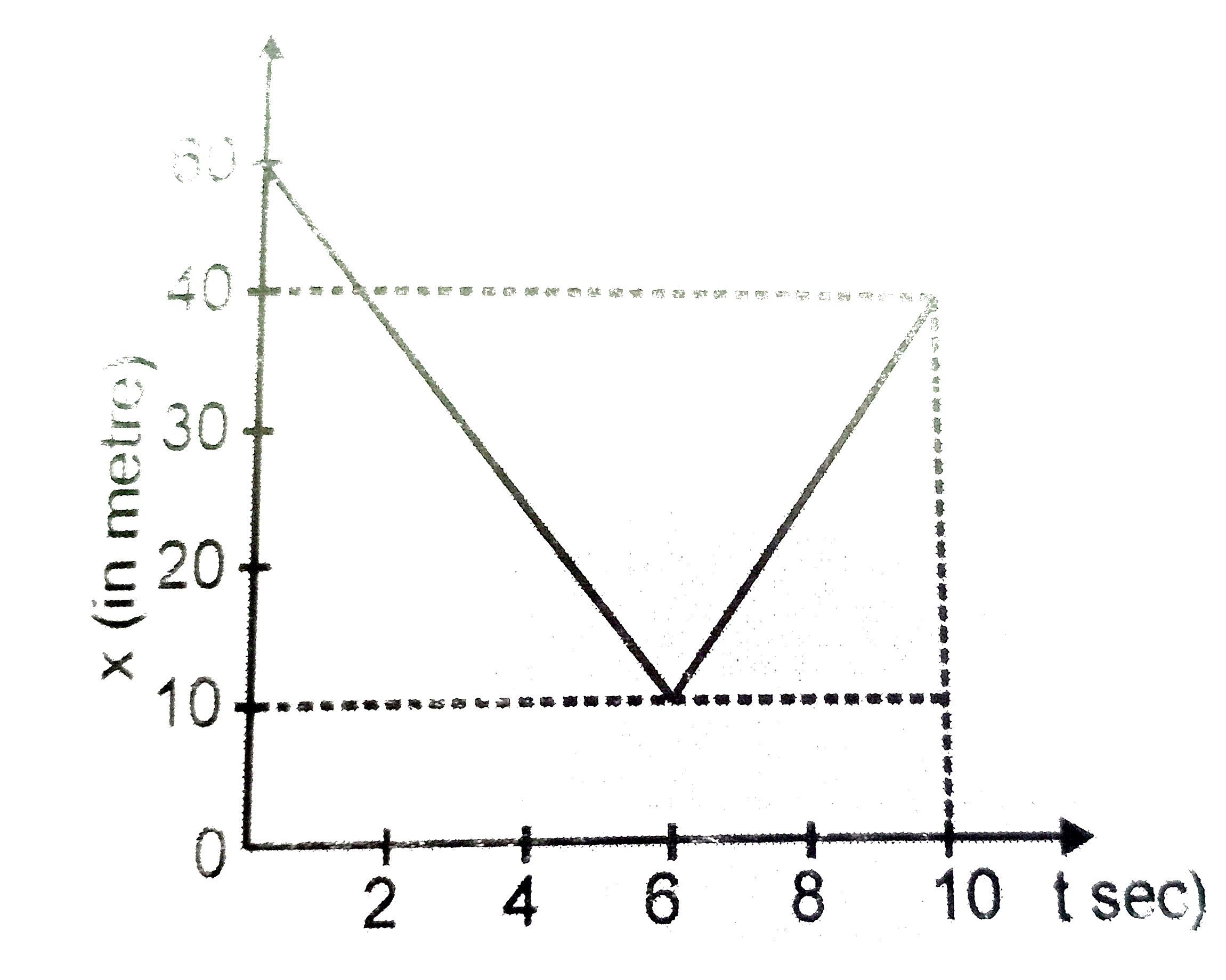
View Solution
