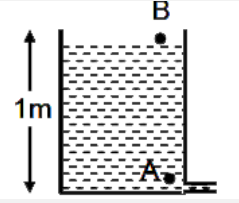
A container of height 10 cm is filled with water. There is hole at bot

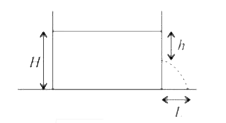
A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :

A $2 \sqrt{h (H - h)}$
B $\sqrt{h (H - h)}$
C $2 \sqrt{\frac{h^{2}}{H - h}}$
D $\sqrt{\frac{h^{2}}{H - h}}$
In a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
Aproportional to h
Bproportional to $h^{1 / 2}$
Cproportional to $h^{2}$
Dindependent of h

A container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .