The manometer has a water column difference of 50 cm . If the atmospheric pressure is 105 Pa, find the pressure of the gas in the container .
To find the pressure of the gas in the container using the given information about the manometer, we can follow these steps:
1. Understand the Manometer Setup:
- A manometer measures the pressure difference between the gas in the container and the atmospheric pressure. The height difference of the water column in the manometer is given as 50 cm.
2. Convert Height to Meters:
- Since the standard unit for height in physics is meters, convert 50 cm to meters:
h=50cm=0.50m
3. Use the Formula for Pressure Difference:
- The pressure difference caused by the height of the water column can be calculated using the formula:
P=ρgh
where:
- ρ is the density of water (approximately 1000kg/m3),
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height of the water column in meters.
4. Calculate the Pressure Difference:
- Substitute the values into the formula:
P=1000kg/m3×9.81m/s2×0.50m
P=4905Pa
5. Determine the Total Pressure in the Container:
- The pressure of the gas in the container (Pgas) can be found by adding the atmospheric pressure (Patm) to the pressure difference (P):
Pgas=Patm+P
- Given that Patm=105Pa:
Pgas=105Pa+4905Pa
Pgas=104905Pa
6. Convert to Kilopascals:
- To express the pressure in kilopascals (kPa):
Pgas=104.905kPa
Final Answer:
The pressure of the gas in the container is approximately 104.905 kPa.
- A manometer measures the pressure difference between the gas in the container and the atmospheric pressure. The height difference of the water column in the manometer is given as 50 cm.
- Since the standard unit for height in physics is meters, convert 50 cm to meters:
h=50cm=0.50m
- The pressure difference caused by the height of the water column can be calculated using the formula:
P=ρgh
where:
- ρ is the density of water (approximately 1000kg/m3),
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height of the water column in meters.
- Substitute the values into the formula:
P=1000kg/m3×9.81m/s2×0.50m
P=4905Pa
- The pressure of the gas in the container (Pgas) can be found by adding the atmospheric pressure (Patm) to the pressure difference (P):
Pgas=Patm+P
- Given that Patm=105Pa:
Pgas=105Pa+4905Pa
Pgas=104905Pa
- To express the pressure in kilopascals (kPa):
Pgas=104.905kPa
The pressure of the gas in the container is approximately 104.905 kPa.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)10videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - SOLVED PROBLEMS (OBJECTIVE )14videos
FLUID MECHANICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
Similar Questions
The heights of mercury surfaces in the tow arms of the manometer shown in figure are 2 cm and 8cm. Atmospheric pressure =1.01×105Nm−2 . Find a. the pressure of the gas in the cylinder and b. the pressure of mercury at the bottom of the U tube.
 View Solution
View SolutionWater is filled in a flask upto a height of 20cm. The bottom of the flask is circular with radius 10cm. If the atmospheric pressure is 1.013×105 Pa, find the force exerted by the water on the bottom . Take g=10ms−2 and density of water =1000kgm−3.
View Solution
Knowledge Check
- Question 1 - Select One
A manometer is connected to gas container. Then the mercury level rises by 2 cm in the arm of the manometer which is not connected to the container.
If the atmospheric pressure is 76 cm of mercury, then the pressure of the gas is ________ cm of mercury.A80B76C72D78 - Question 2 - Select One
An iar tight container having a lid with negli-gible mass and an area of 8cm2 is partially evacuated. If a 48 N forces is required to pull the lig of the container and the atmospheric pressure is 1.0×105Pa the pressure in the container before it is opened must be
A0.6 atmB0.5 atmC0.4 atmD0.2 atm
Water is filled in a flask up top a heightof 20 cm. The bottom of the flask is circular with radius 10 cm.If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
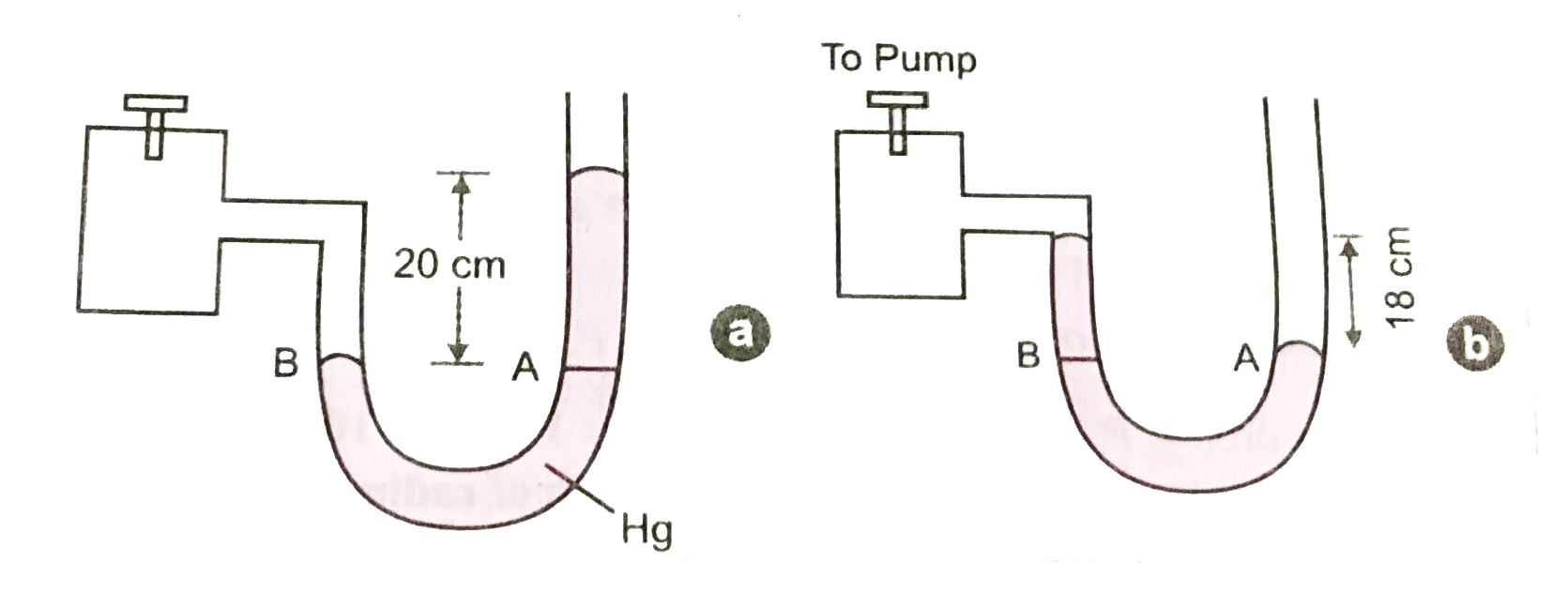
View SolutionA manometer reads the pressure of a gas in a enclosure as shown in figure(a) When some of the gas is removed by a pump, the manometer reads as in (b). The liquid used in the manometers is mercury and the atmospheric pressure is 76cm of mercury.

(i) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b) in units of cm of mercury .
(ii) How would the level change in case (b) if 13.6cm of water are poured into the right limb of the manometer?View SolutionA manometer reads the pressure of a gas in an encloure as shown in fig. when some of the gas is removed by the pump, the manometer reads as in fig. the liquid used in mano-meters is mercury and the atmospheric pressure is 76 cm of mercury.
(i) Given the absolute and gauge pressure of the gas in the two cases (in units of cm. of mercury).
(ii) How would the levels change in case(b) if 13.6cm of water are poured into the right limb of manometer? (Ignore the change in volume of the gas).
 View Solution
View SolutionA gas is filled into a bulb connected to an open limb manometer. The level of mercury in the open arm is 2.1 cm lower than that in the other arm of the manometer. The atmospheric pressure is 740 mm. What is the pressure of the gas?
View SolutionA manometer is connected to a gas containing bulb. The open arm reads 43.7cm whereas the arm connected to the bulb reads 15.6cm. If the barometric pressure is 743mm mercury , calculate the pressure of the gas in bar?
Strategy : The pressure of the gas inside the bulb is greater than the external atmospheric pressure because the height of mercury column in the left arm is less than in the right arm.Therefore ,
pgas(in cm)=patom(in cm)+hcmView SolutionA gas is filled into a bulb connected to an open limb manometer. The level of mercury in the open arm is 2.1 cm lower than that in the other arm of the manometer. The atmospheric pressure is 740 mm. What is the pressure of the gas?
View Solution

