नीचे की आकृति में केन्द्र O वाले एक चाप पर तीन बिन्दु A,B और C इस प्रकार है की ∠BOC=30∘ तथा ∠AOB=60∘ है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है तो ∠ADC ज्ञात कीजिए।
प्रश्न से ∠AOB+∠BOC=60∘+30∘=90∘
∴∠AOC=90∘
चूँकि किसी वृत्त में केन्द्र का कोण उसके एकान्तर वृत्तखंड के कोण का दुगुना होता है,
इसलिए ∠AOC=2∠ADC
∴∠ADC=12∠AOC=12×90∘=45∘

Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - वृत्त EXERCISE - EXERCISE 12.1 (अतिलघु उत्तरीय प्रश्न )29videos
वृत्त
- BOOK - KC SINHACHAPTER - वृत्त EXERCISE - EXERCISE 12.1 (लघु उत्तरीय प्रश्न )5videos
वृत्त
- BOOK - KC SINHACHAPTER - वास्तविक संख्याओं पर संक्रियाएँ एवं वास्तविक संख्याओं के घातांक EXERCISE - Objective Questions30videos
वास्तविक संख्याओं पर संक्रियाएँ एवं वास्तविक संख्याओं के घातांक
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न9videos
समांतर चतुर्भुज
Similar Questions
तीन अरैखिक बिन्दुओं से कितने वृत्त खींचे जा सकते है ।
04:04View Solutionबगल के चित्र में O वृत्त के केन्द्र है ∠OBA=25∘ एवं ∠OCA=35∘ है, तो, ∠BAC ज्ञात करे।
05:04View Solutionपरिमेय संख्या का दशमलव प्रसार कैसा होता है?
04:21View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
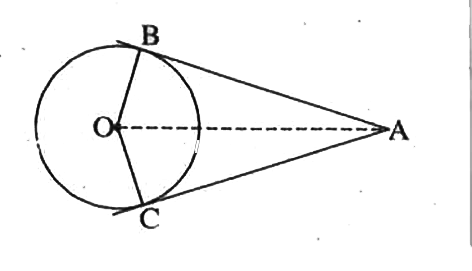
06:54View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
 05:05View Solution
05:05View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।
 05:37View Solution
05:37View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
04:32View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
02:29View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
04:26View Solutionएक दीर्घवृत्त जिसका केन्द्र मूलबिंदु पर है, की उत्केंद्रता 12 है। यदि उसकी एक नियता x=-4 है, तो उसके बिन्दु (1,32) पर उसके अभिलम्ब का समीकरण है
04:06View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:29View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
07:49View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
05:40View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
02:01View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
05:04View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
02:05View Solution

