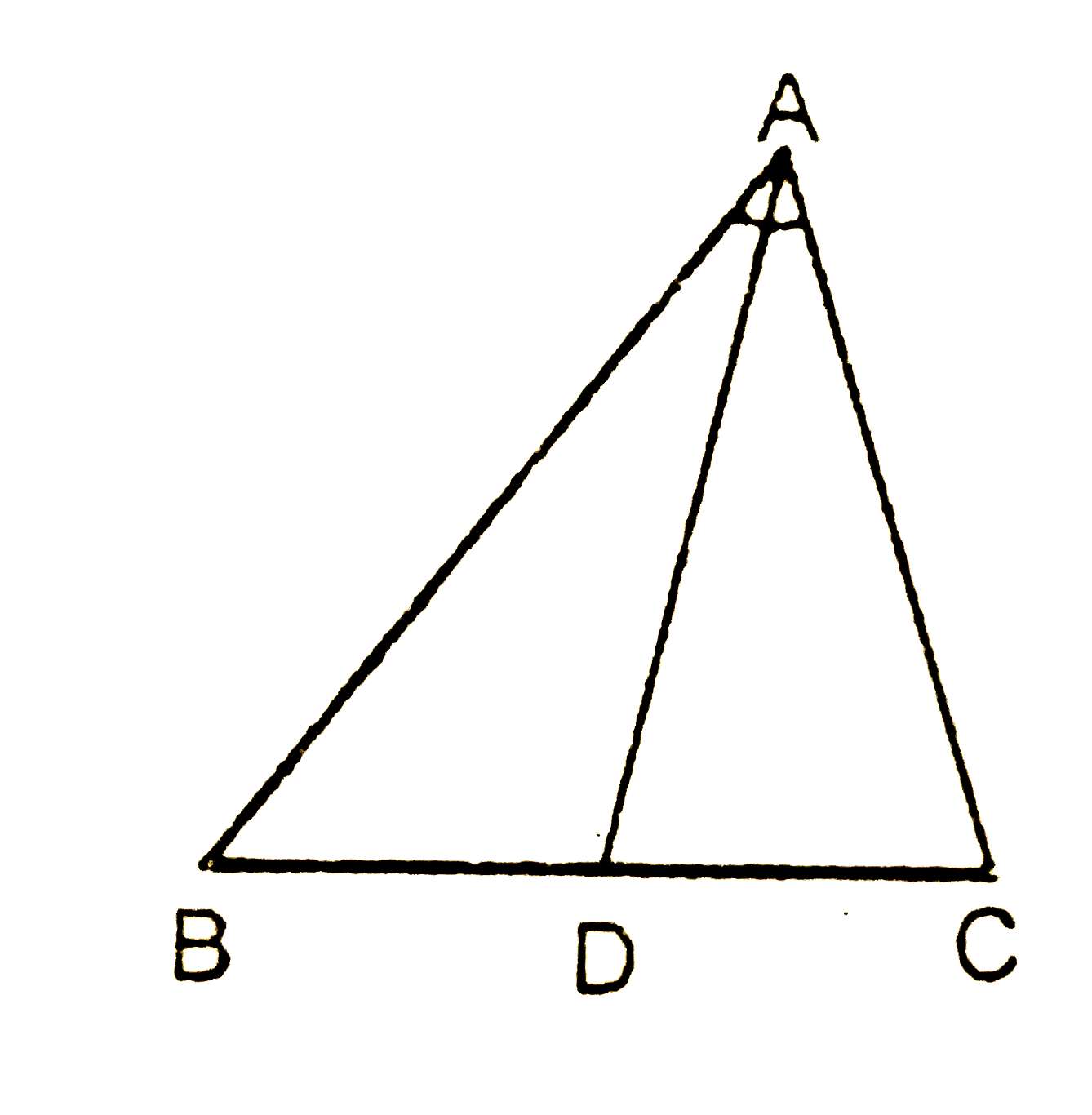
दिए गये चित्र में , ΔABC की भुजा BC पर D इस प्रकार है कि ∠ADC=∠BAC. सिद्ध करें कि CA2=CB×CD.
दिया है : ΔABC में ,D भुजा BC पर एक बिन्दु इस प्रकार है कि ∠ADC=∠BAC.
सिद्ध करना है : CA2=CB×CD
उपपत्ति : ΔABC और ΔDAC में
∠BAC=∠ADC ( दिया हुआ है )
∠ACB=∠DCA ( उभयनिष्ट)
अतः ΔABC~ΔDAC (A A समरूपता से)
इसलिए ΔABC और ΔDAC की भुजाएँ समानुपाती है ।
⇒CACB=CDCA
⇒CA2=CB×CD (प्रमाणित)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)02:34View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
02:24View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..03:01View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
01:56View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
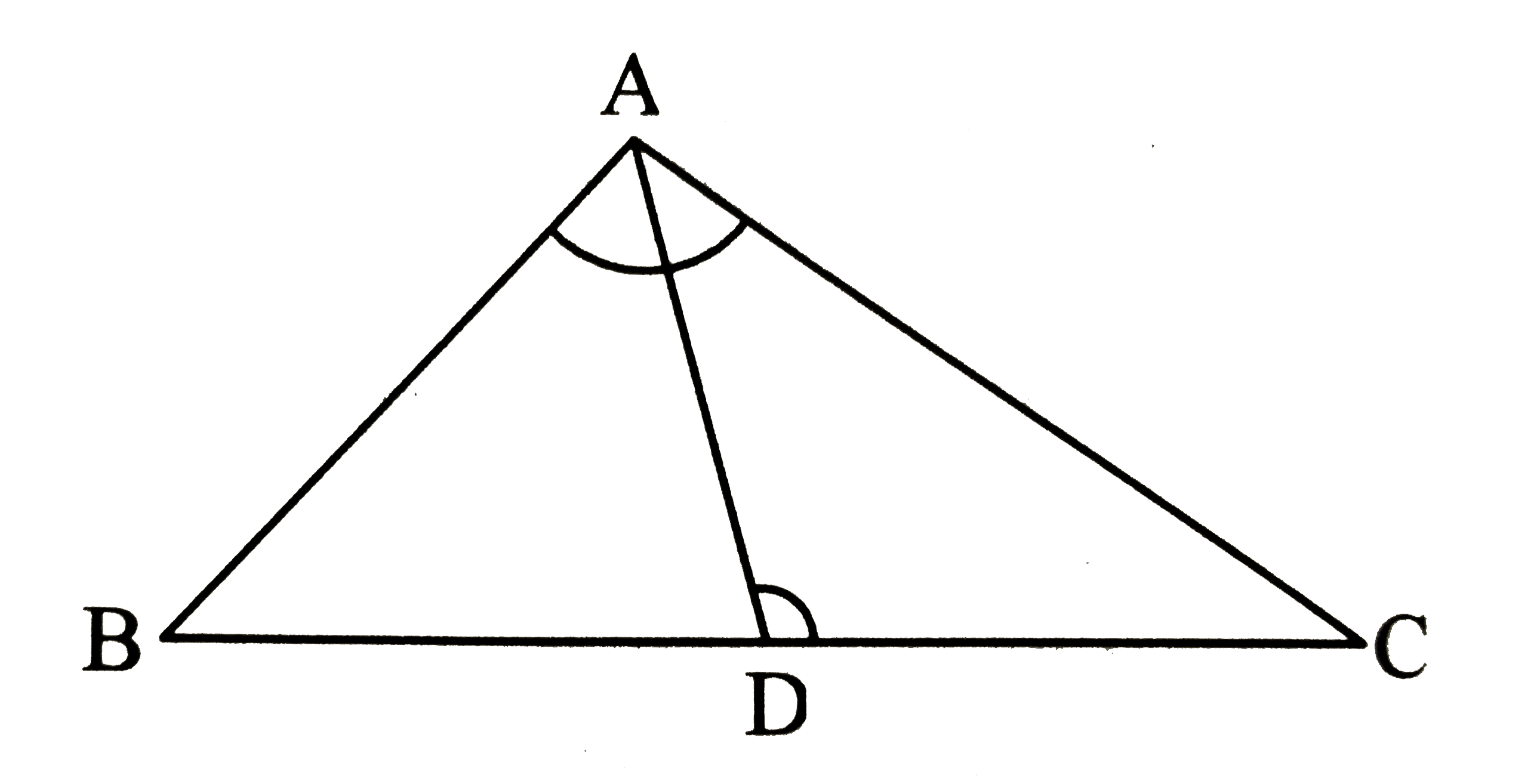
03:21View SolutionIn the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
 02:50View Solution
02:50View SolutionΔABC की भुजा BC पर एक बिंदु D इस प्रकार है कि है ∠ADC=∠BAC सिद्ध कीजिये कि CA2=CB×CD
02:42View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।
 02:09View Solution
02:09View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
02:39View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
02:56View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
02:19View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
01:24View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में वर्धमान है ।
f(x)=logsinx,x∈(0,π2)01:33View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=x2−2x+3,x<101:38View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए हुए अन्तराल में ह्रासमान है -
f(x)=x2−2x+3,x<101:30View Solutionदिये गये चित्र में स्पर्श रेखा है -
 05:15View Solution
05:15View Solution

