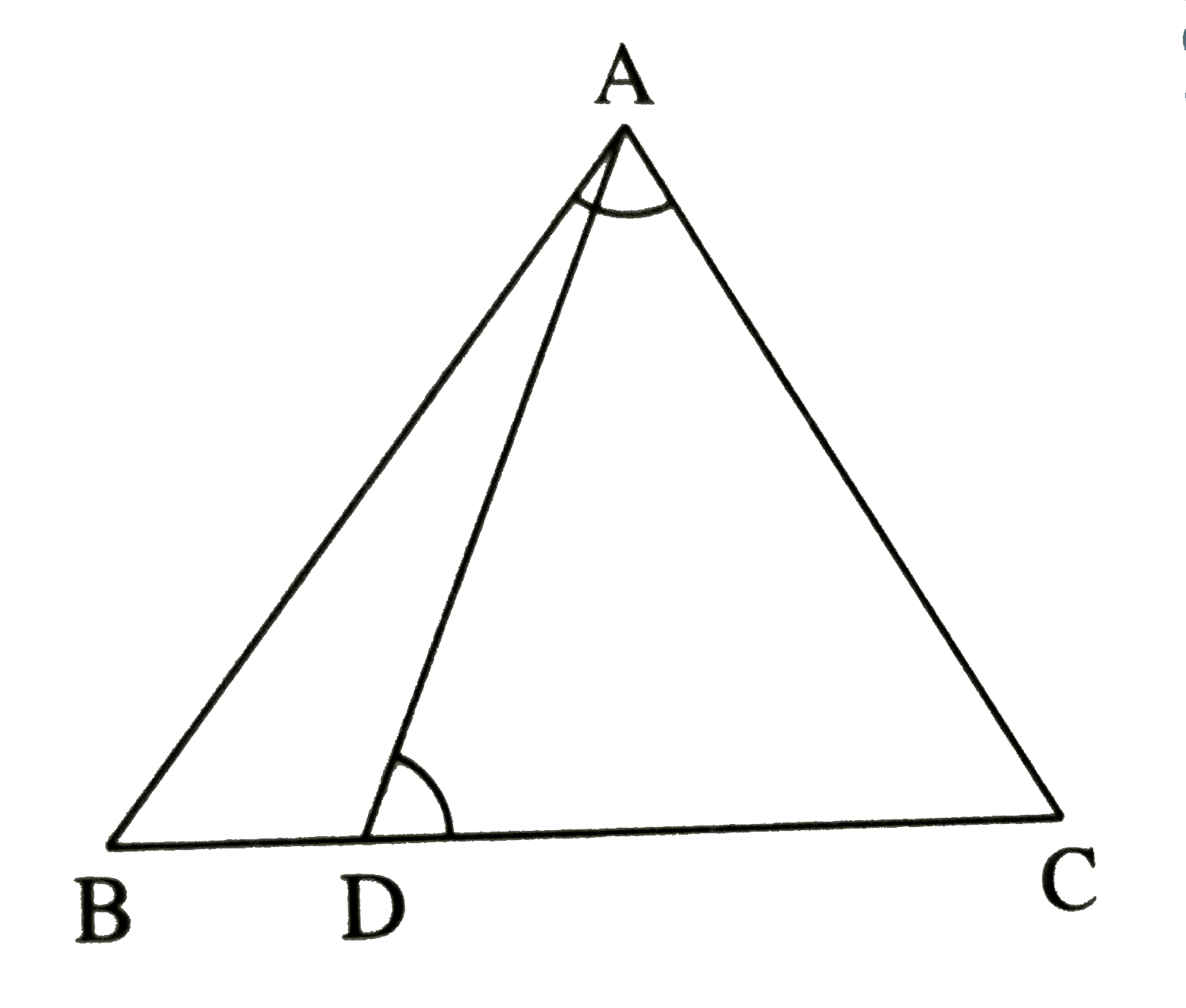
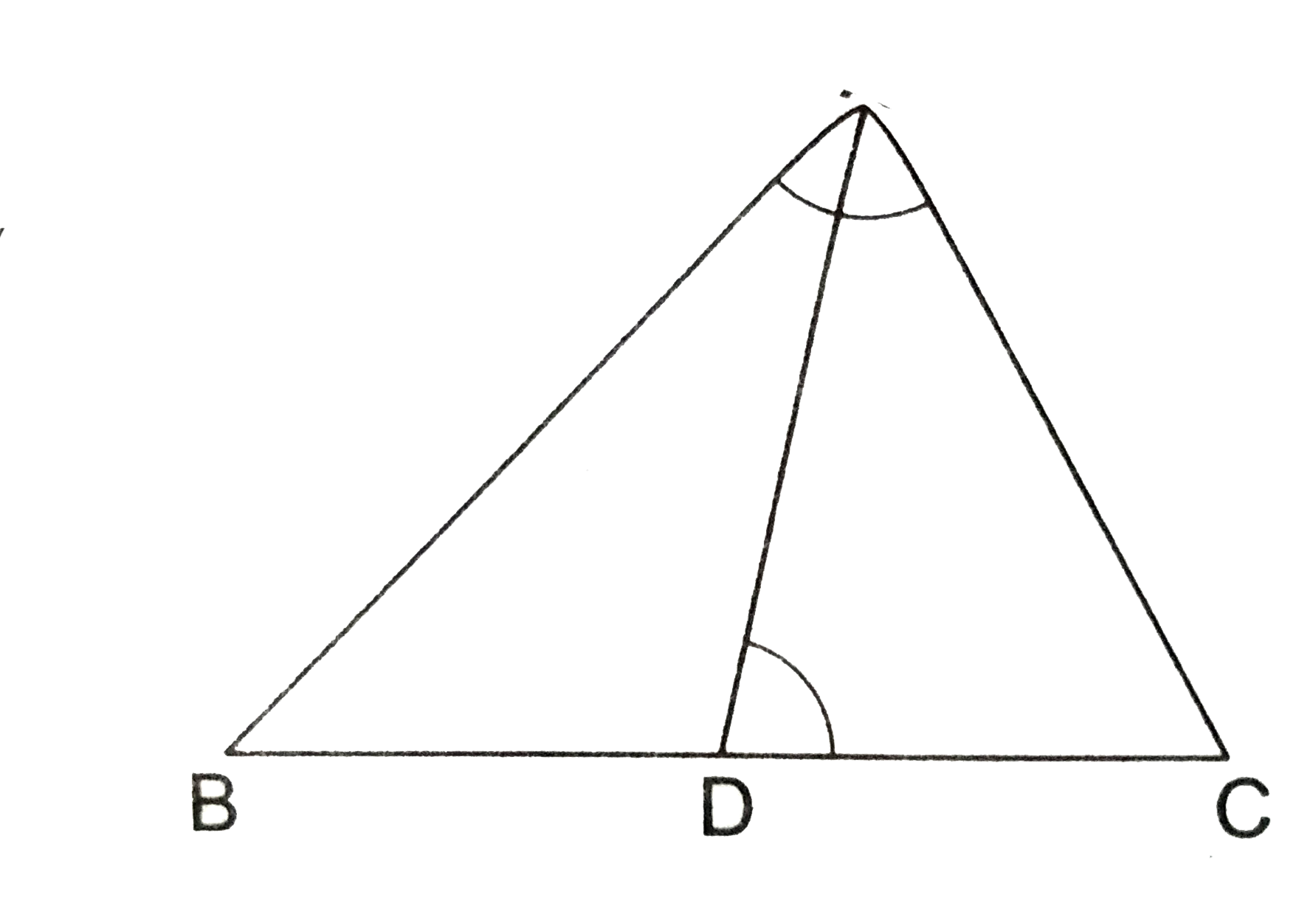
In the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
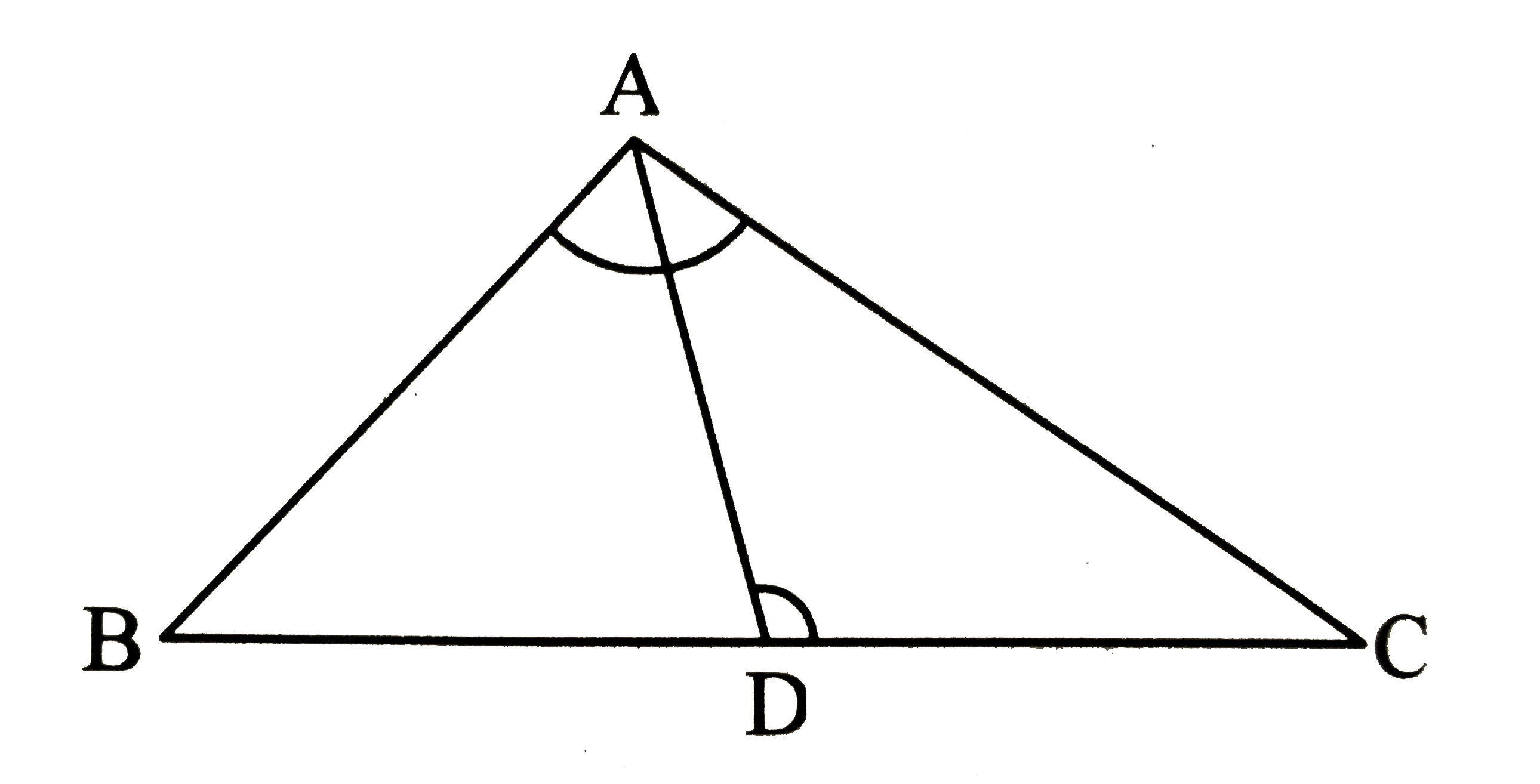
The correct Answer is:∴ CA2=CB×CD
Step by step video & image solution for In the adjoining figure, in DeltaABC, point D is on side BC such that, angleBAC = angleADC. Prove that, CA^2 = CB xx CD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.4
7 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Problem Set - 1
19 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.2
11 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
Knowledge Check
In ΔABC, D is a point on side BC such that ∠ADC=∠BAC, If CA = 12 cm, CB = 8 cm then CD is equal to :
A18 cmB12 cmC16 cmD15 cmIn the adjoining figure of ΔABC,∠BCA=120∘andAB=c,BC=a,AC=b then:
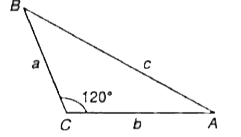 Ac2=a2+b2+baBc2=a2+b2−baCc2=a2+b2−2baDc2=a2+b2+2ab
Ac2=a2+b2+baBc2=a2+b2−baCc2=a2+b2−2baDc2=a2+b2+2ab
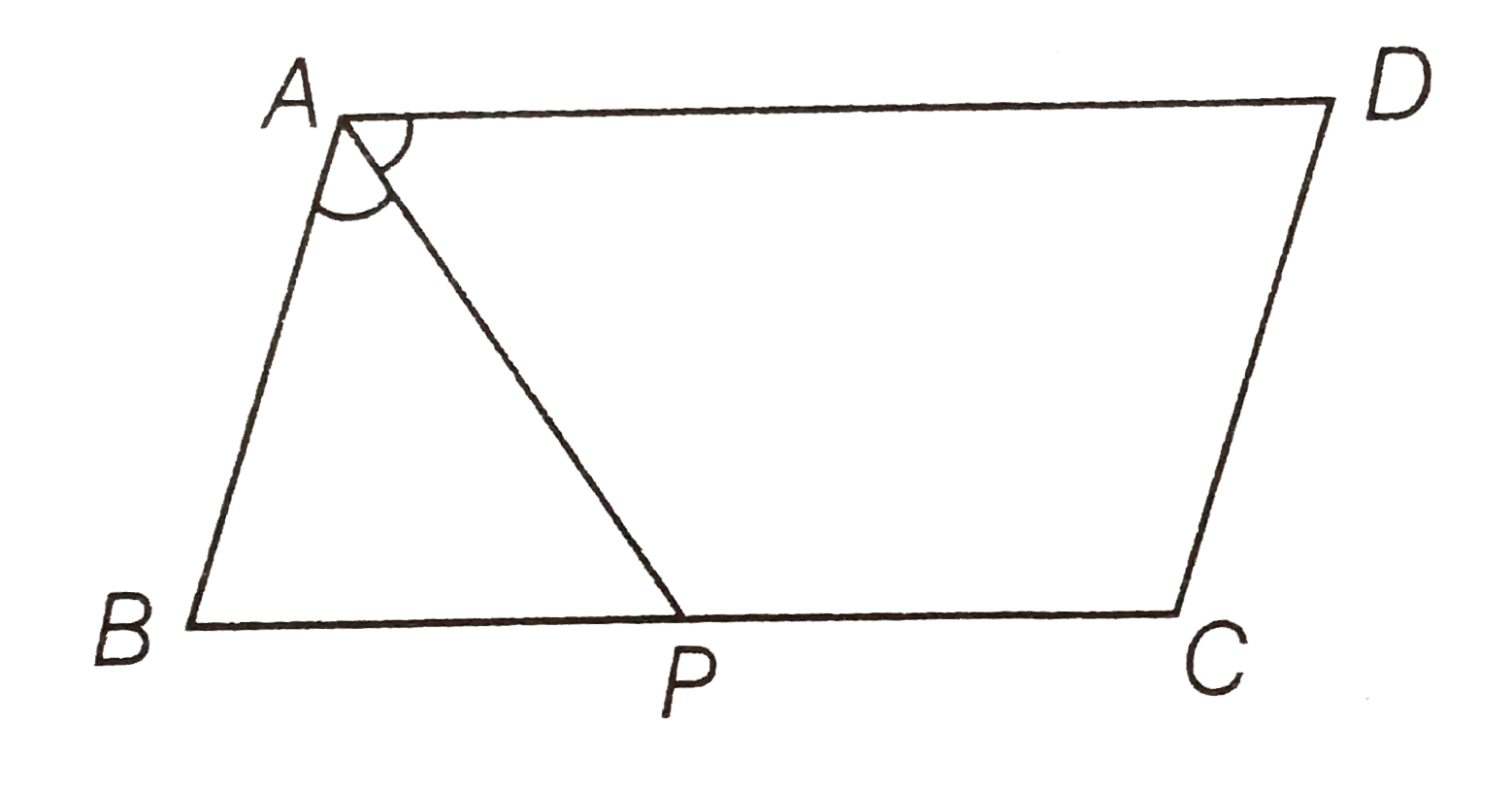
In the given figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
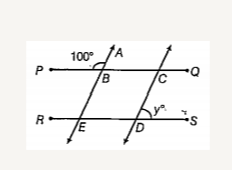
View SolutionIn the adjoining figure AE||CD and BC||ED, then find Y.
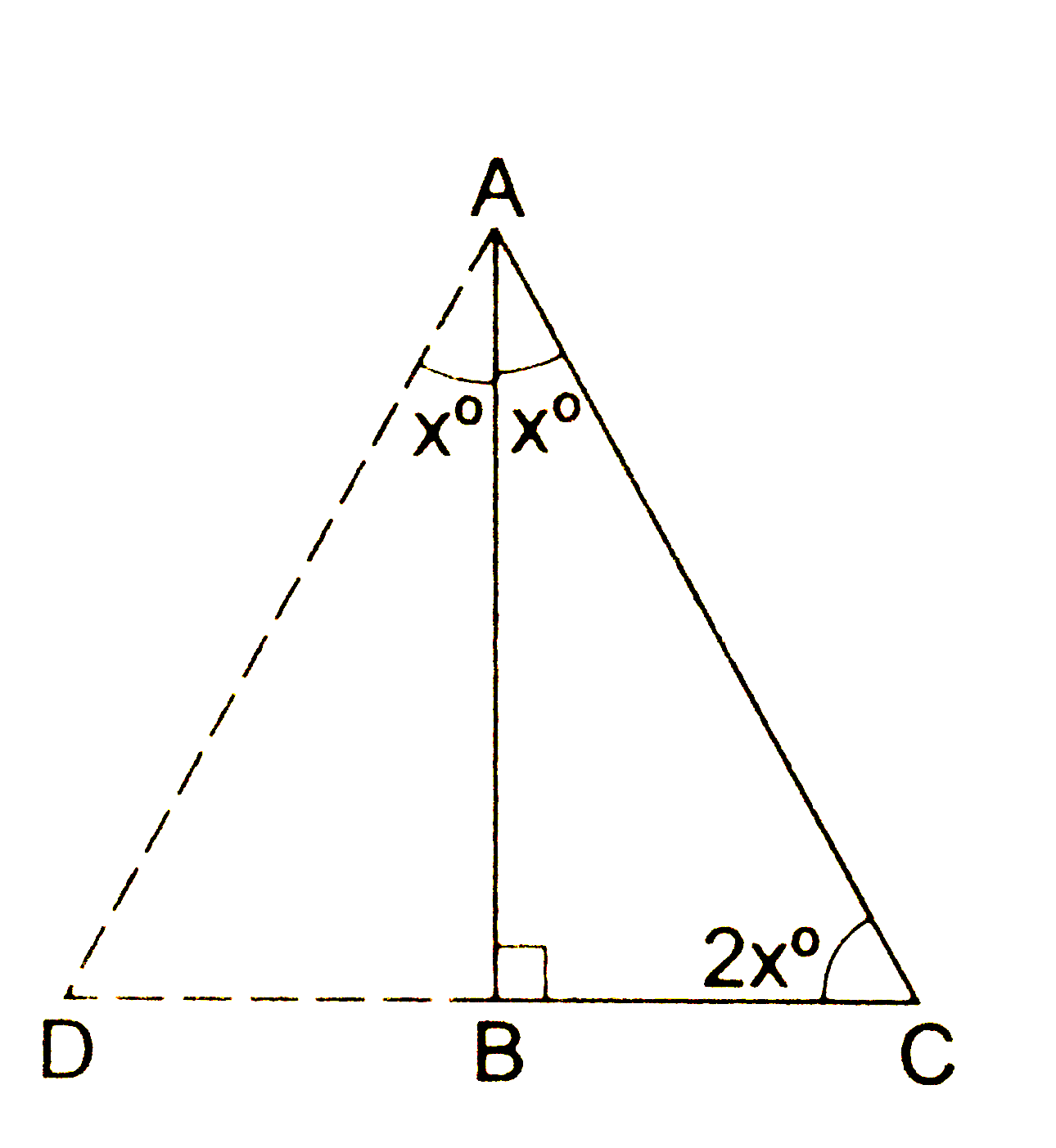
View SolutionIn the given figure, ΔABC is right angled at B such that ∠BCA=2∠BAC. Show that hypotenuse AC = 2BC.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD. ltBrgt
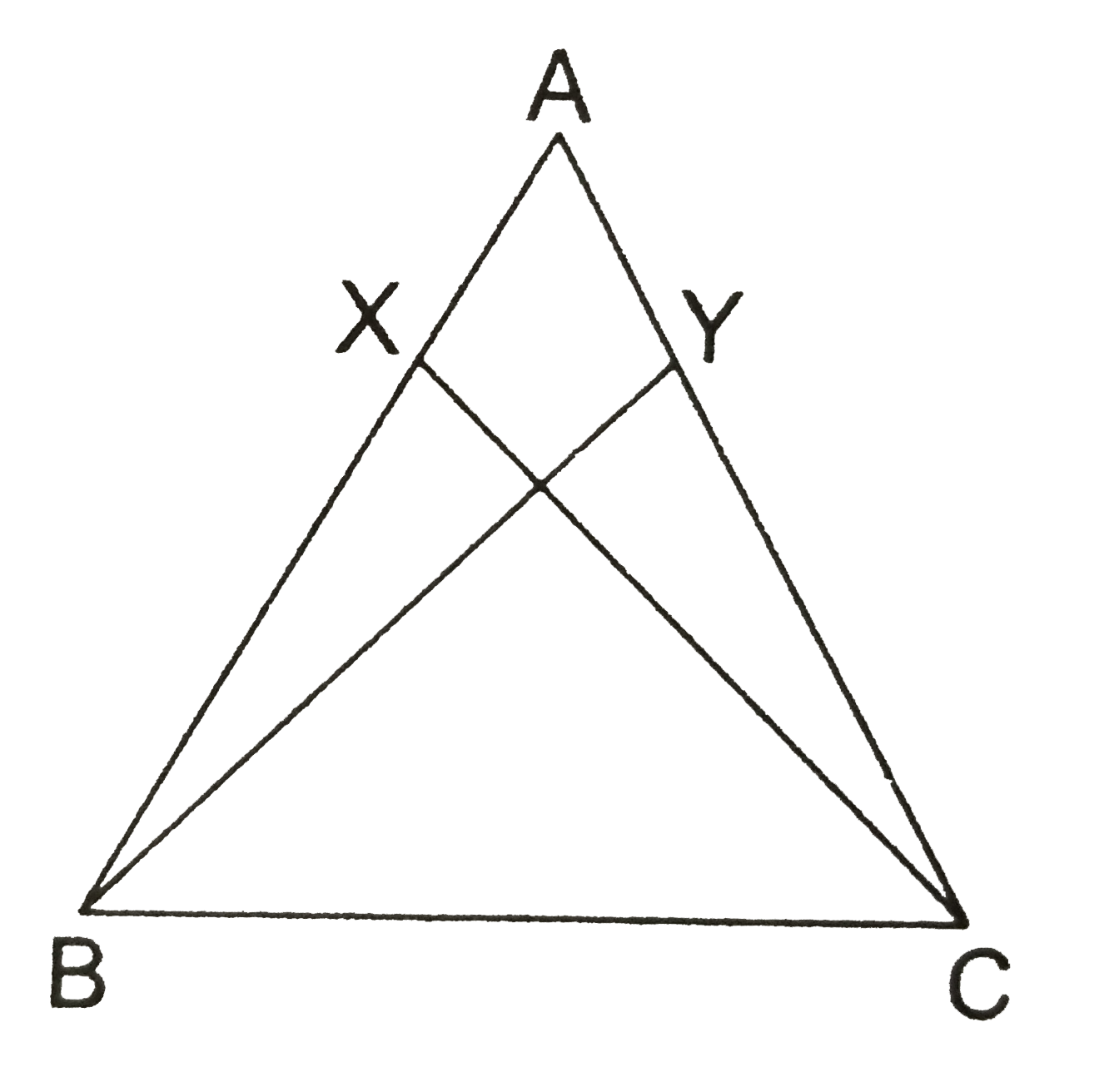
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
View Solution