सिद्ध कीजिए कि एक वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उस वर्ग के विकर्ण पर बने वर्ग के क्षेत्रफल से आधा होता है ।
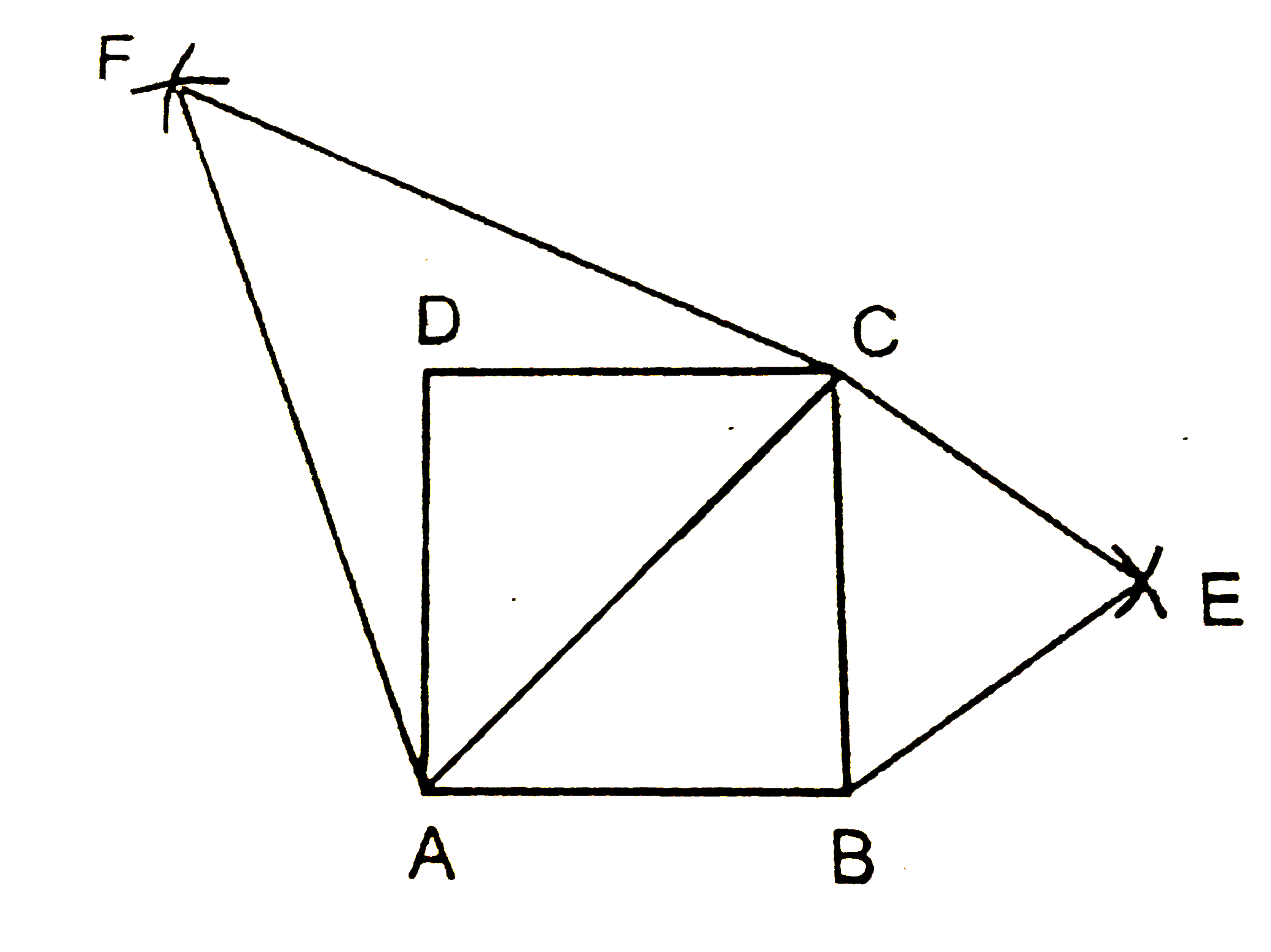
ABCD एक वर्ग है और ΔBCE तथा ΔACF समबाहु त्रिभुज क्रमशः भुजा BC और कर्ण AC पर बनाये गये है ।
सिद्ध करना है : क्षे०(ΔBCE)=12क्षे०(ΔACF)
उपपत्ति : चूँकि ΔBCE और ΔACF में , प्रत्येक समबाहु त्रिभुज है ।
इसलिए उनमे से प्रत्येक का प्रत्येक कोण 60∘ है ।
∴ΔBCE और ΔACF समानकोणीक है ।
⇒ΔBCE~ΔACF
चूँकि दो समरूप त्रिभुजों के क्षेत्रफलों के अनुपात , उनके संगत भुजाओं के वर्गों के अनुपात के बराबर होता है ।
∴क्षे०(ΔBCE)क्षे०(ΔACF)=BC2AC2=BC22(B)2 [∵AC=√2BC]
=12
अतः क्षे०(ΔBCE)=12क्षे०(ΔACF)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)03:24View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
03:53View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..04:02View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
02:36View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
02:26View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
06:27View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
03:05View Solutionउस रसाल रेखा का समीकरण ज्ञात कीजिए जो अक्षो पर समान अन्तः खण्ड काटे तथा रेखा अक्षो से घिरे त्रिभुज का क्षेत्रफल 8 वर्ग मात्रक हो।
03:59View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
04:01View Solutionउन रेखाओं का समीकरण जिन पर मूल बिन्दु से डाला गया। लम्ब x-अक्ष के साथ 30∘ का कोण बनाता है और उनसे तथा x-अक्ष से बने त्रिभुज का क्षेत्रफल 50√3 वर्ग इकाई हो, है
01:33View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
01:31View SolutionThe area of a regular hexagon is equal to the area of the square. What is the ratio of the perimeter of the regular hexagon to the perimeter of square? सम षटभुज का क्षेत्रफल वर्ग के क्षेत्रफल के बराबर है। सम षटभुज के परिमाप का वर्ग के परिमाप से क्या अनुपात है?
01:16View SolutionThe area of square is 200m^2 . A new square is formed in such a way that the length of its diagonal is sqrt2 times of the given square. Then the area of the new square formed is- एक वर्ग का क्षेत्रफल 200 वर्ग मीटर है। एक नया वर्ग इस प्रकार बनाया गया है कि उसके विकर्ण की लंबाई पहले वर्ग के विकर्ण की sqrt2 गुना के बराबर है, नये वर्ग का क्षेत्रफल है-
03:46View SolutionThe length of diagonal of a square whose area is 64m2 is:
उस वर्ग के विकर्ण की लंबाई ज्ञात करें जिसका क्षेत्रफल 64 वर्ग मीटर है|03:50View SolutionThe area of a square is 144 cm^2 . What is the perimeter of the square formed by the diagonal of the original square as its side? एक वर्ग का क्षेत्रफल 144 वर्ग सेमी है| आरंभिक वर्ग के विकर्ण को भुजा मानकर बनाए गए वर्ग का परिमाप क्या होगा ?
03:36View SolutionThe diagonal of a square measures 6√2 cm. The measure of the diagonal of a square whose area is twice that of the first square is:
किसी वर्ग का विकर्ण 6√2 सेमी का है | उस वर्ग के विकर्ण का माप ज्ञात करें जिसका क्षेत्रफल पहले वर्ग के क्षेत्रफल से दोगुना है ?37:41View Solution

