The area of a regular hexagon is equal to the area of the square. What is the ratio of the perimeter of the regular hexagon to the
perimeter of square?
सम षटभुज का क्षेत्रफल वर्ग के क्षेत्रफल के बराबर है। सम षटभुज के परिमाप का वर्ग के परिमाप से क्या अनुपात है?
√6√3:√3√6
2√3:√6√2
√6√3:2
√6:2√√3
To solve the problem, we need to find the ratio of the perimeter of a regular hexagon to the perimeter of a square, given that their areas are equal.
1. Area of a Regular Hexagon:
The area Ah of a regular hexagon with side length a is given by the formula:
Ah=3√32a2
2. Area of a Square:
The area As of a square with side length b is given by the formula:
As=b2
3. Setting the Areas Equal:
According to the problem, the area of the hexagon is equal to the area of the square:
3√32a2=b2
4. Finding the Ratio of Side Lengths:
Rearranging the equation gives:
a2b2=23√3
Taking the square root of both sides, we find:
ab=√23√3
5. Calculating the Perimeters:
The perimeter Ph of the regular hexagon is:
Ph=6a
The perimeter Ps of the square is:
Ps=4b
6. Finding the Ratio of Perimeters:
Now, we can find the ratio of the perimeters:
PhPs=6a4b=3a2b
Substituting ab from step 4 into this equation:
PhPs=32⋅√23√3
7. Simplifying the Ratio:
Now we simplify 32⋅√23√3:
=32⋅√2√3√3=3√22√3√3
Further simplifying gives:
=3√22⋅31/4⋅31/2=3√22⋅33/4
8. Final Ratio:
The final ratio of the perimeter of the regular hexagon to the perimeter of the square is:
3√22⋅33/4
The area Ah of a regular hexagon with side length a is given by the formula:
Ah=3√32a2
The area As of a square with side length b is given by the formula:
As=b2
According to the problem, the area of the hexagon is equal to the area of the square:
3√32a2=b2
Rearranging the equation gives:
a2b2=23√3
Taking the square root of both sides, we find:
ab=√23√3
The perimeter Ph of the regular hexagon is:
Ph=6a
The perimeter Ps of the square is:
Ps=4b
Now, we can find the ratio of the perimeters:
PhPs=6a4b=3a2b
Substituting ab from step 4 into this equation:
PhPs=32⋅√23√3
Now we simplify 32⋅√23√3:
=32⋅√2√3√3=3√22√3√3
Further simplifying gives:
=3√22⋅31/4⋅31/2=3√22⋅33/4
The final ratio of the perimeter of the regular hexagon to the perimeter of the square is:
3√22⋅33/4
Topper's Solved these Questions
Similar Questions
Knowledge Check
A square and a regular hexagon have equal perimeters. Their areas are in the ratio:
A2:1B2√3:1C√3:2D3:2The ratio of the area of a square to the area of a regular hexagon, having the same perimeter is:
A2:3B√3:2C1:√3D4:3√3The radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
A2:πB1:πCπ:1Dπ:2
The area of a square is 144cm2. What is the perimeter of the square formed by the diagonal of the original square as its side?
एक वर्ग का क्षेत्रफल 144 वर्ग सेमी है| आरंभिक वर्ग के विकर्ण को भुजा मानकर बनाए गए वर्ग का परिमाप क्या होगा ?
View SolutionThe area of a circle and a square are same. The ratio of the diagonal of the square to the radius of the circle is-
एक वृत्त और एक वर्ग का क्षेत्रफल एकसमान है। वर्ग की विकर्ण और वृत्त की त्रिज्या का अनुपात क्या होगा?
View SolutionIn the given figure, the ratio of the area of the largest square to that of the smallest square is:
दी गयी आकृति में, सबसे बड़े वर्ग के क्षेत्रफल और सबसे छोटा वर्ग के क्षेत्रफल का अनुपात है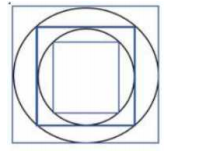
View SolutionIf the area of an equilateral triangle is 36√3cm2, then the perimeter of the triangle is:
यदि एक समबाहु त्रिभुज का क्षेत्रफल 36√3 वर्ग सेमी है, तो इस त्रिभुज का परिमाप कितना होगा ?
View SolutionABCDEF is a regular hexagon. What is the ratio of the area of triangle ACE and area of triangle AEF?
ABCDEF एक सम षटभुज है। त्रिभुज ACE के क्षेत्रफल तथा त्रिभुज AEF के क्षेत्रफल का अनुपात क्या है?
View Solution
