आयत ABCD के अन्दर O एक बिन्दु है । सिद्ध करें कि OB2+OD2=OA2+OC2
दिया है : O, आयत ,ABCD के भीतर एक बिन्दु है ।
सिद्ध करना है कि OB2+OD2=OA2+OC2
रचना : O से POQ∣∣BC खींचा जो AB पर तथा P को Q पर काटता है ।
उपपत्ति : चूँकि POQ∣∣BC
∴PQ⊥AB और PQ⊥DC
अब ∠BPQ=90∘ और ∠CQP=90∘
∴BPQCऔर APQD दोनों आयत है ।
∴BP=CQ [आयत की सम्मुख भुजाएँ ]
और DQ=AP [आयत की सम्मुख भुजाएँ]
समकोण ΔOPB से , OB2=OP2+BP2 .....(i)
समकोण ΔOQD से , OD2=OQ2+DQ2 .....(ii)
समकोण ΔOPA से , OA2=OP2+AP2 ....(iii)
समकोण ΔOQC से, OC2=OQ2+CQ2....(iv)
(i) और (ii), को जोड़ने पर हम पाते है, OB2+OD2=OP2+BP2+DQ2
=OP2+OQ2+CQ2+AP2 [∵BP=CQ और DQ=AP]
=(OP2+AP2)+(OQ2+CQ2)
=OA2+OC2
[(iii) और (iv) से]
अतः OB2+OD2=OA2+OC2 .

Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View Solutionआयत ABCD के अंदर स्थित O कोई बिंदु है सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है

View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
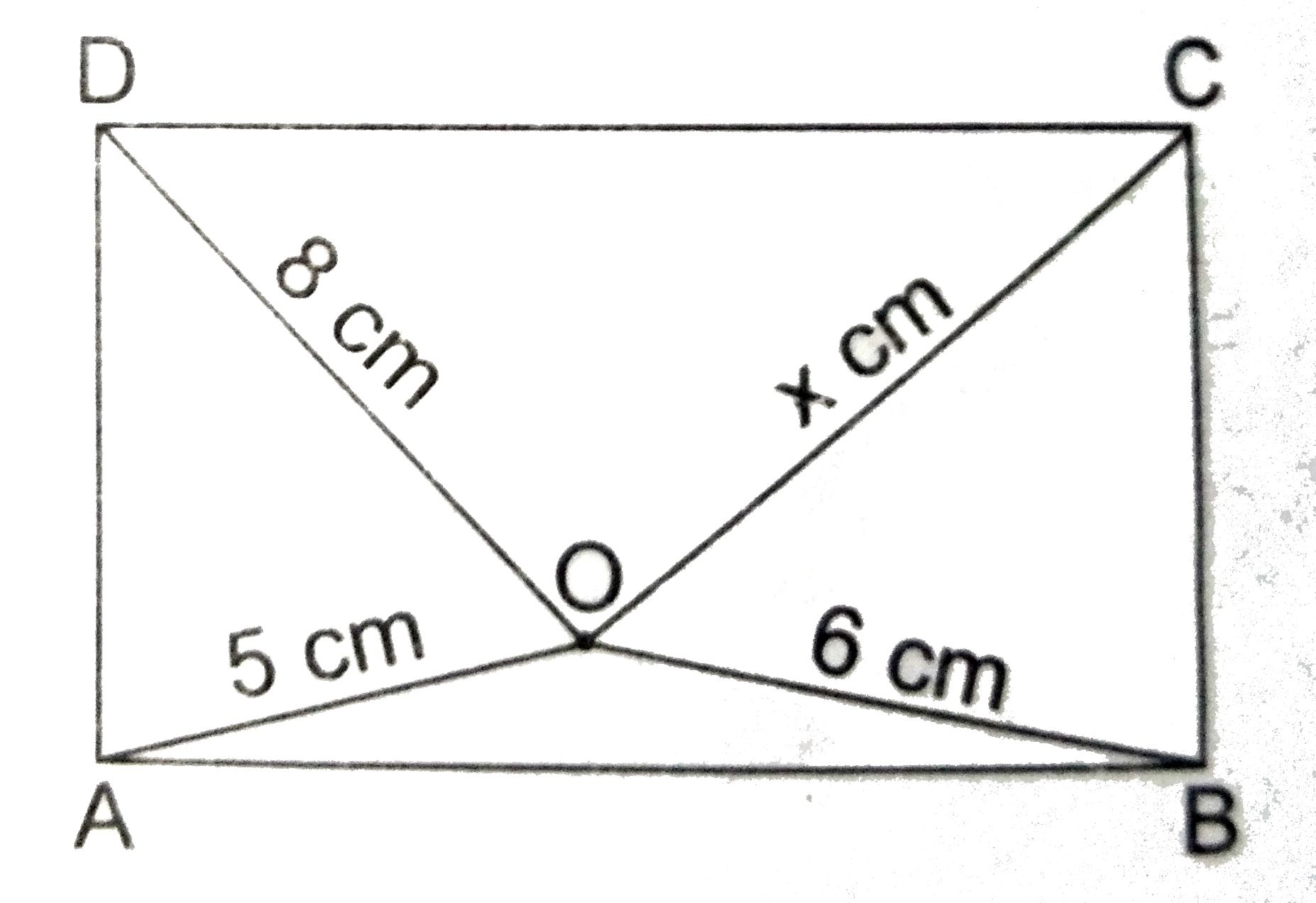
View Solutionआयतन ABCD के अंदर स्थित O कोई बिन्दु है । सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है ।
View SolutionO is any point inside a rectangle ABCD, Prove that OA2+OC2=OB2+OD2
View SolutionIn figure O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionO' is any point inside a rectangle ABCD.
Prove that OB2+OD2=OA2+OC2
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View SolutionIf 'O' is any point in the interior of rectangle ABCD, then prove that : OB^(2) + OD^(2) = OA^(2) + OC^(2)
View Solutionபடத்தில் O என்பது செவ்வகம் ABCD யில் உள்ளே உள்ள எனில் ,OB2+OD2=OA2+OC2என நிரூபிக்க ?
View Solutionధీరగా చతురస్రం ABCD అంతరంలో ఏదైనా బిందువు 'O' అయితే OB2+OD2=OA2+OC2 అని చూపండి.
View Solution‘O’ is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2
View Solution
