86. a, b care the sides of a rightandangled triangle and a circle of radiusr touches the sides of the triangle. If cis the hypotenuse of the triangle,then the value of r is:a + b + C(1)a + b + ca +b-c87. If one zero of the quadraticnolynomial d+ 15x + 6 is reciprocal

Video Solution

Answer

Step by step video & image solution for 86. a, b care the sides of a rightandangled triangle and a circle of radiusr touches the sides of the triangle. If cis the hypotenuse of the triangle,then the value of r is:a + b + C(1)a + b + ca +b-c87. If one zero of the quadraticnolynomial d+ 15x + 6 is reciprocal by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS REAL NUMBERS

Knowledge Check

The sides of a right triangle ABC are a, b and c, where c is the hypotenuse. What will be the radius of the in circle of this triangle?
A $\frac{(a + b + c)}{2}$
B $\frac{(a + b - c)}{2}$
C $\frac{(b + c - a)}{2}$
D $\frac{(a + c - b)}{2}$
If a, b,c are the lengths of the sides of triangle , then
A $a - b > c$
B $a + b < c$
C $c = a + b$
D $c < a + b$
In a right-angled triangle with sides a and b, hypotenuse c, the altitude drawn on the hypotenuse is x. Then
A $a b = x^{2}$
B $\frac{1}{a} + \frac{1}{b} = \frac{1}{x}$
C $a^{2} + b^{2} = 2 x^{2}$
D $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{x^{2}}$

86. a, b care the sides of a rightandangled triangle and a circle of radiusr touches the sides of the triangle. If cis the hypotenuse of the triangle,then the value of r is:a + b + C(1)a + b + ca +b-c87. If one zero of the quadraticnolynomial d+ 15x + 6 is reciprocal

Similar Questions

Knowledge Check

The sides of a right triangle ABC are a, b and c, where c is the hypotenuse. What will be the radius of the in circle of this triangle?

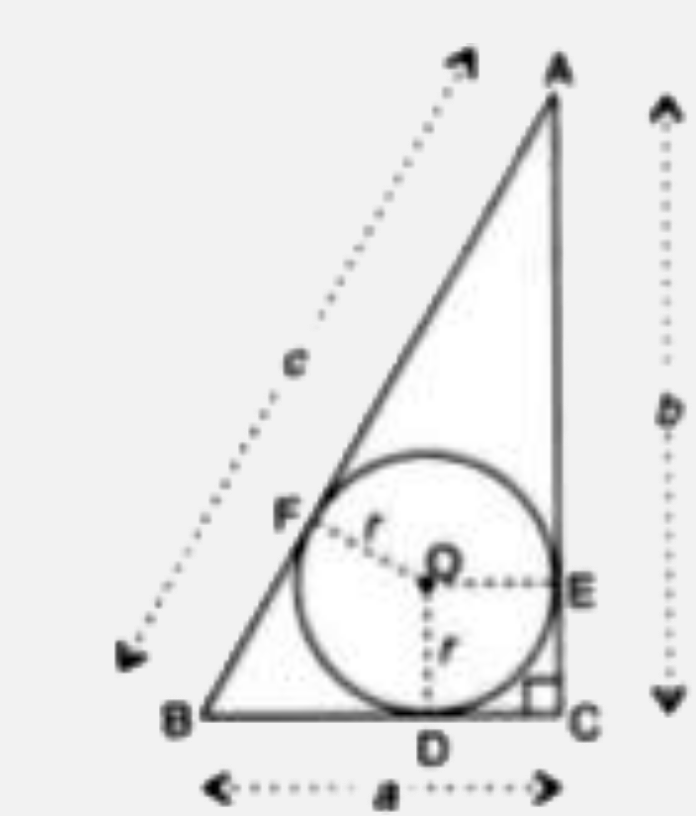
If a, b,c are the lengths of the sides of triangle , then

In a right-angled triangle with sides a and b, hypotenuse c, the altitude drawn on the hypotenuse is x. Then

Recommended Questions