If a,b and c are sides of a ritht triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r=a+b−c2.
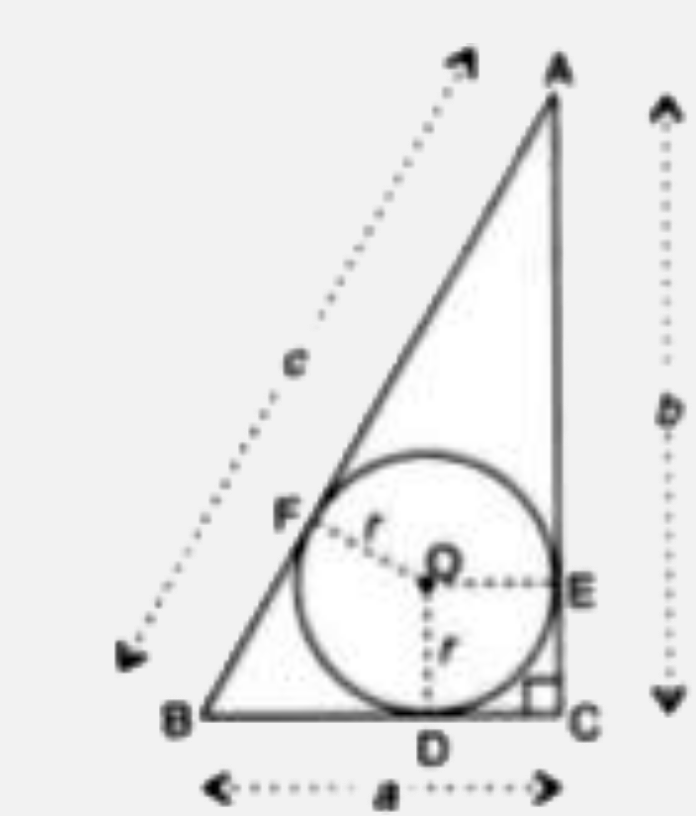
Step by step video & image solution for If a,b and c are sides of a ritht triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r = (a + b-c)/(2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If a,b,c are the sides of a right triangle , where c is the hypotenuse. Prove that the radius r of the circle which touches the sides of the triangle is given by:r=a+b−c2
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View SolutionDraw a right triangle whose hypotenuse is of length 4 cm and one side is of length 2.5 cm.
View SolutionDEF is the triangle formed by joining the points of contact of the incircle with the sides of the triangle ABC, prove that its sides are 2rcosA2, 2rcosB2 and 2rcosC2 where r is the radius of incircle of ABC. its angles are π2−A2,π2−B2andπ2−C2 its area is r2s2R where 's' is the semiperimter and R is the circumradius of the ABC .
View Solution(c) 103 (d) 10 18. A circle is inscribed in an equilateral triangle with side lengths 6 unit. Another circle is drawn inside the triangle (but outside the first circle), tangent to the first circle and two of the sides of the triangle. The radius of the smaller circle is (b) 2/3 (a) 1/ root3 (c) 2 (d) 1
View SolutionIf in a triangle ABC,cosA+2cosB+cosC=2 prove that the sides of the triangle are in AP
View Solutiona, b and c are the integral sides of a right angled triangle in which c is the hypotenuse measuring 3√5 metres. If side 'a' is increased by 4003% and side 'b' is increased by
503%, then their total becomes 14 metres. Find the area of triangle.
View SolutionIf ABC is an isosceles triangle with AB=AC . Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View Solution
