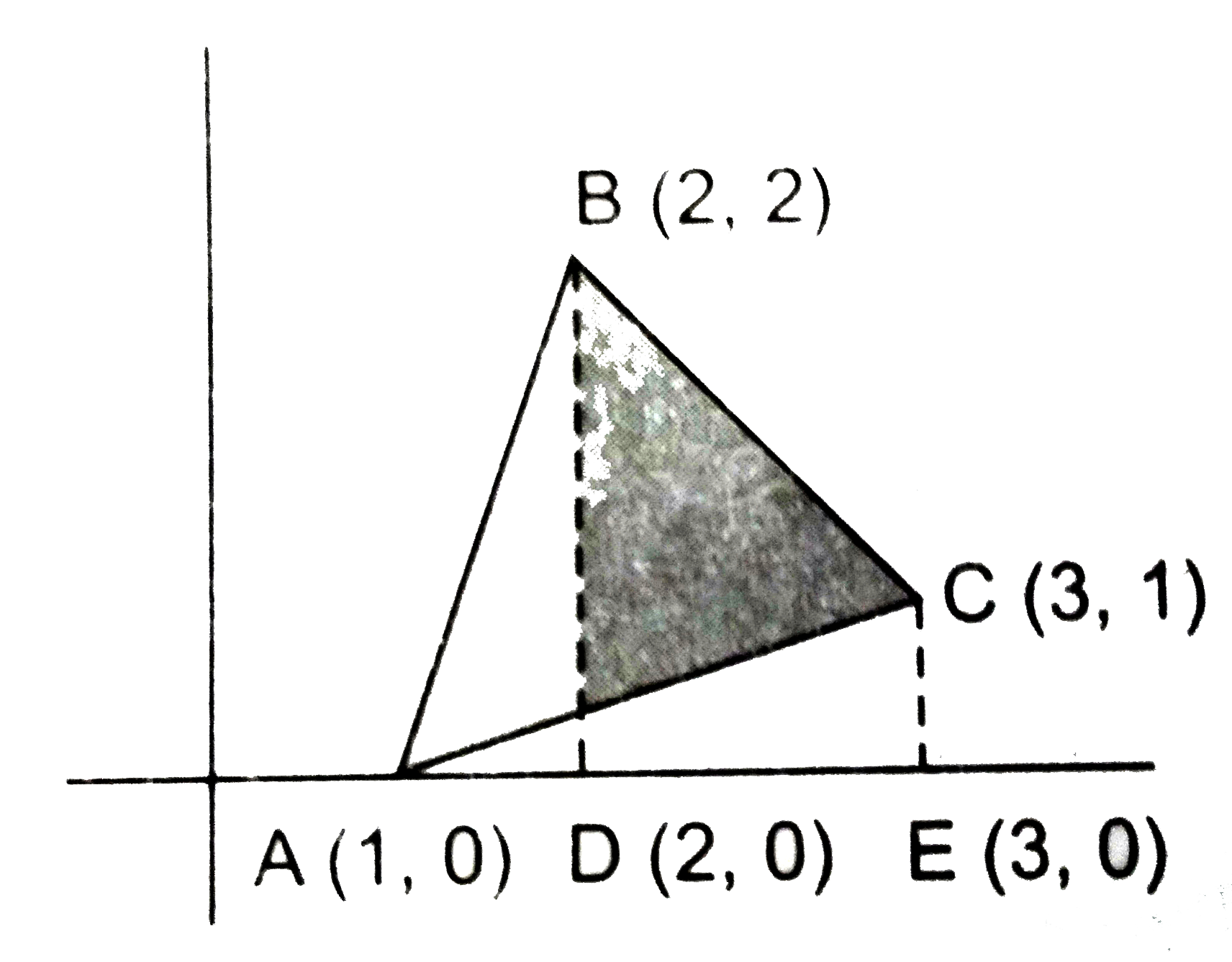
निशिचत समाकलन की सहायता से त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(1,0),B(2,2) और C(3,1) है|
AB का समीकरण
y−0=2−02−1(x−1)
⇒ y=2x−2
BC का समीकरण
y−2=13=1−23−2(x−2)
⇒ y=4−x.
y−2=1−23−2(x−2)
⇒ y=4−x
AC का समीकरण
y−0=1−03−1(x−1)
⇒ y=12(x−1)
अब ΔABC का क्षेत्रफल
= ΔABD का क्षेत्रफल + □DBCE का क्षेत्रफल - ΔACE का क्षेत्रफल .
=∫21(2x−2)dx+∫32(4−x)dx−∫3112(x−1)dx
=[x2−2x]21+[4x−x22]32−12[x22−x]31.
=[(4−4)−(1−2)+[(12−92)−(8−2)]−12[(92−3)−(12−1)]
=1+152−6−34−14=32 वर्ग इकाई
Topper's Solved these Questions
- समाकलनो के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - समाकलनो के अनुप्रयोग EXERCISE - प्रश्नावली 8A
28 Videos
- समाकलनो के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - समाकलनो के अनुप्रयोग EXERCISE - प्रश्नावली 8B (बहुविकल्पीय प्रश्न)
1 Videos
- समाकलन BOOK - NOOTAN HINDICHAPTER - समाकलन EXERCISE - विविध प्रश्नावली
44 Videos
- सम्बन्ध एवं फलन BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - विविध प्रश्नावली
19 Videos
Similar Questions
सरल रेखा y=mx,X- अक्ष और X =2 के बीच के भगा का क्षेत्रफल निशिचत समाकलन की सहायता से ज्ञात कीजिए ।
View Solutionपरवलय y2=4ax और सरल रेखा y=2ax के बीच घिरे भाग का क्षेत्रफल है-
View Solution1x−x3
View Solutionमान लीजिए कि f:R→R,f(x)=10x+7 द्वारा परिभाषित फलन है । एक ऐसा फलन g:R→R ज्ञात कीजिए जिसके लिए gof=fog=IR हो ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionत्रिभुज ABC की मध्याकाओं की लम्बाई ज्ञात कीजिए, जिसके शीर्ष A(3, -2), B(0, 6) और C(-2, 4) है ।
View Solutionयदि सदिश 10¯i−5¯j+10¯k किस त्रिभुज के आधार को निरूपित करता है तथा इस आधार की सम्मुख शीर्ष से दूरी 8 मात्रक हो तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionउस त्रिभुज के परिकेन्द्र और परिवृत्त की त्रिज्या ज्ञात कीजिए जिसके शीर्ष क्रमश :(4,6),(0,4) और (6,2) है ।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View SolutionA(a,0) और B(−a,0)दो स्थिर बिंदु है । त्रिभुज ABC के शीर्ष C का बिन्दुपथ ज्ञात कीजिए यदि ∠A−∠B=θ.
View Solutionउस त्रिभुज का अतः केंद्र ज्ञात कीजिए जिसके शीर्षों के निर्देशांक (1,2),(2,3) और (3,1) है ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solution
