सदिश विधि से $Δ A B C$ में सिद्ध कीजिए कि -
(i) $cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$
$(i i) a = b cos C + c cos B$

Video Solution

Text Solution

Verified by Experts

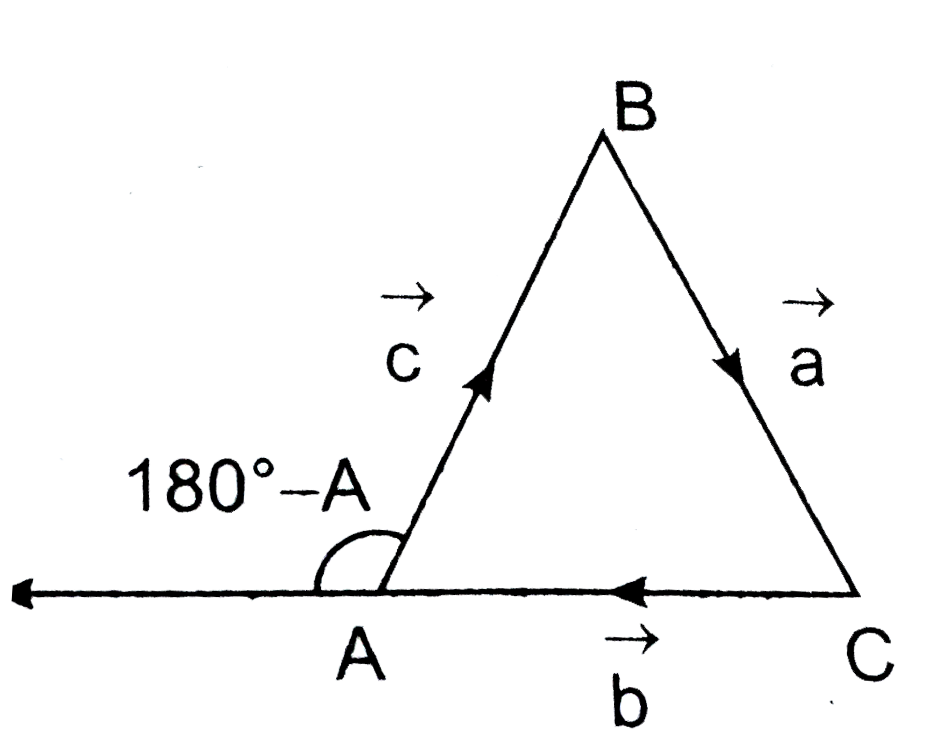
$Δ A B C$ में ,
$- - \to B C + - - \to C A + - - \to A B = \to 0$
$\Rightarrow \to a + \to b + \to c = \to 0$ …(1)
(i) $\to a + \to b + \to c = \to 0$
$\Rightarrow \to b + \to c = - \to a$
$\Rightarrow (\to b + \to c) . (\to b + \to c) = (- \to a) . (- \to a)$
$\Rightarrow {∣ ∣ \to b ∣ ∣}^{2} + {| \to c |}^{2} + 2 \to b . \to c = {| \to a |}^{2}$
$\Rightarrow b^{2} + c^{2} - 2 b c cos A = a^{2}$
$\Rightarrow cos A = a^{2}$
$\Rightarrow cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$
( जहाँ $| \to a | = a, ∣ ∣ \to b ∣ ∣ = b, | \to c | = c)$
$(i i)$ पुन : $\to a + \to b + \to c = \to 0$
$\Rightarrow \to a . (\to a + \to b + \to c) = \to a . \to 0$
$\Rightarrow \to a . \to a + \to a . \to b + \to a . \to c = 0$
$\Rightarrow | \to a | | \to a | {cos 0}^{\circ} + | \to a | ∣ ∣ \to b ∣ ∣ cos (180^{\circ} - C) + | \to a | | \to c | cos (180^{\circ} - B) = 0$
$\Rightarrow a^{2} - a b cos C - a c cos B = 0$
$\Rightarrow a = b cos C + c cos B$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-सदिश एवं सदिशों का गुणन -विविध प्रश्नावली

Home
Ask Doubt
Profile