In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
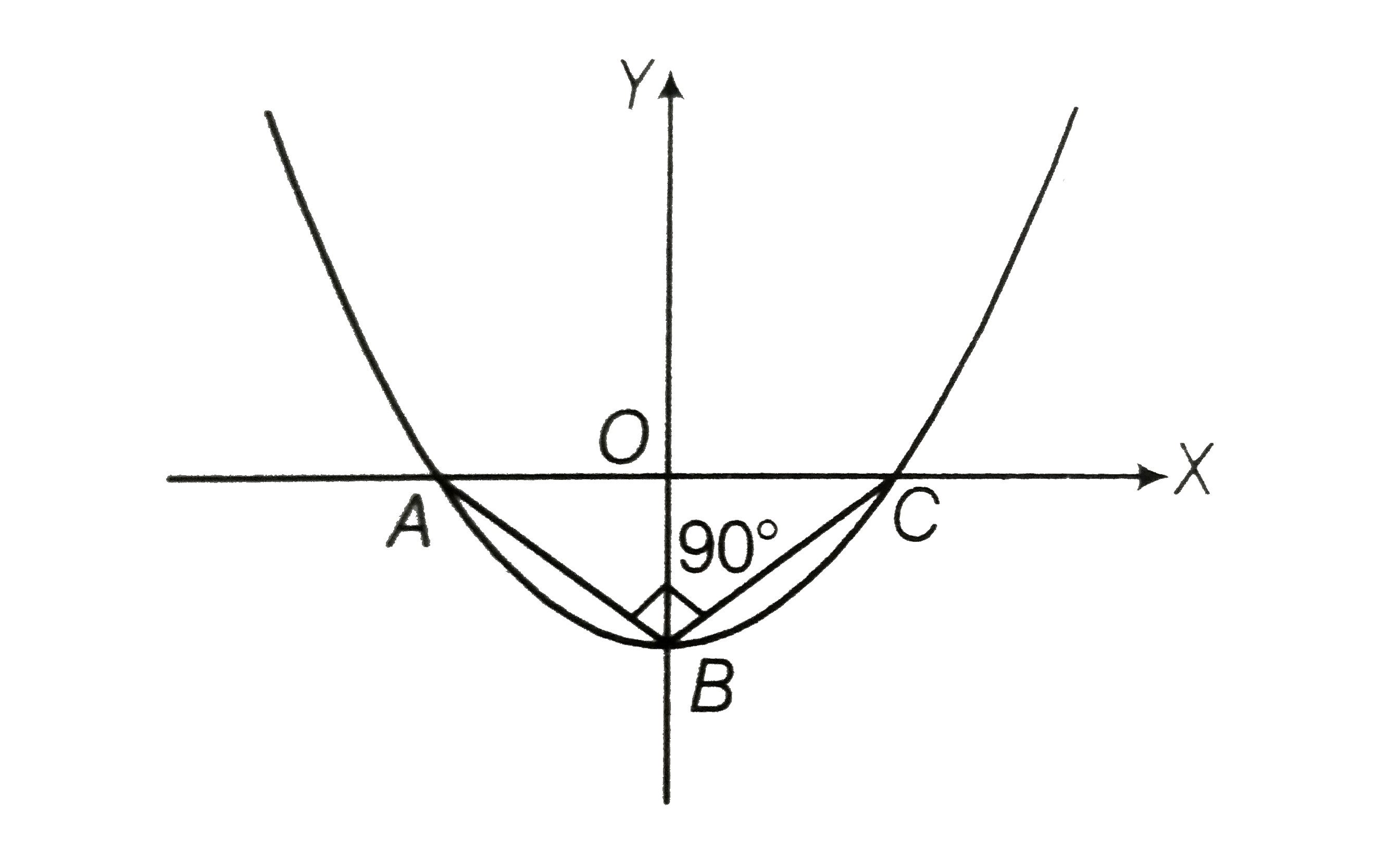
Minimum valueof y=f(x) is
−4√2
−2√2
0
2√2
The correct Answer is:B
Given that AC=4√2 units
∴AB=BC=AC√2=4 units andd OB=√(BC)2−(OC)2
=√(4)2−(2√2)2[∵OC=AC2]
=2√2 units
∴ Vertices are A=(−2√2,0),
B=−(0,−2√2)
and C=(2√2,0)
Minimum value of y=x22√2−2√2 is at x=0
∴(y)min=−2√2
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single Integer Answer Type Questions)10videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matching Type Questions)2videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
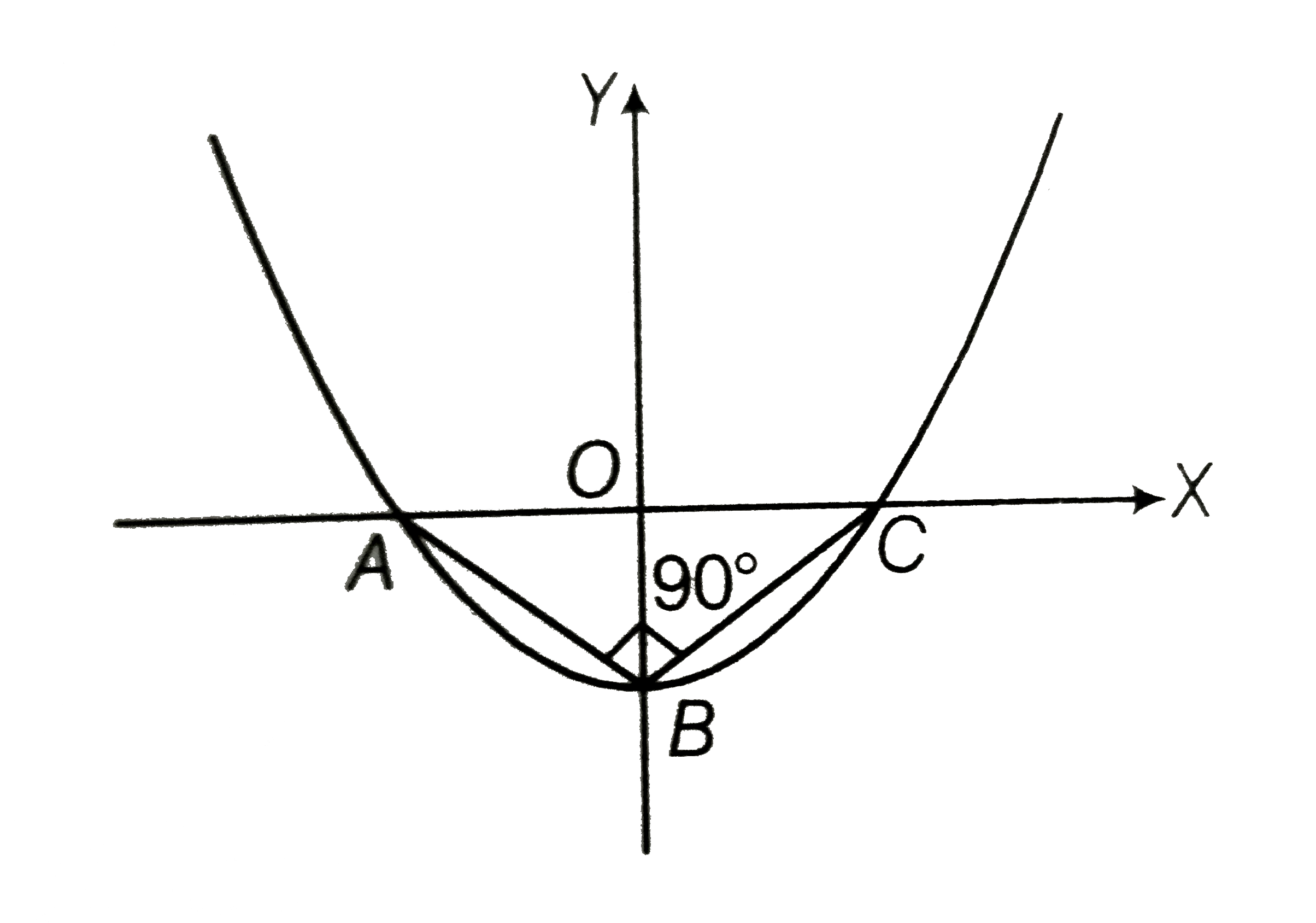
y=f(x) is given byView SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
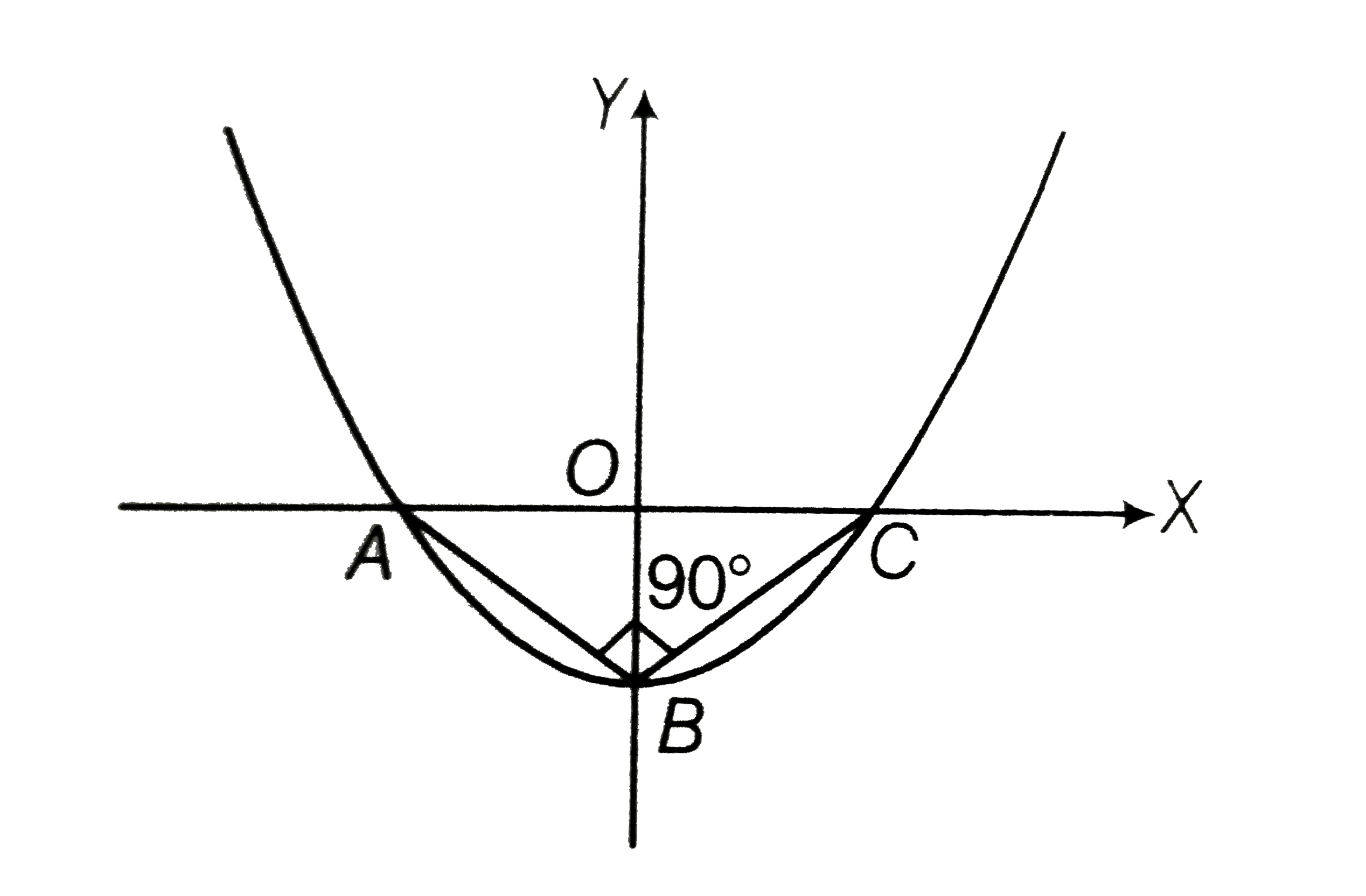
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, isView Solution
Knowledge Check
- Question 1 - Select One
What is the area of a right angled isosceles triangle whose hypotenuse is 6√2cm?
A12 cm2B18 cm2C24 cm2D36 cm2
In the given figure, vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units. Number of integral values of k for which one root of f(x)=0 is more than k and other less than k
View SolutionWhat is the area of a right angled isosceles triangle whose hypotenuse is 6√2cm?
View SolutionFind the area of a right isosceles triangle whose hypotenuse is 16√2 cm.
View SolutionFind the area of a right isosceles triangle whose hypotenuse is 16√2 cm.
View SolutionFind the area of an isosceles right triangle whose hypotenuse is 4√2 cm
View SolutionIn the given figure, ΔABC is right angled at B such that ∠BCA=2∠BAC. Show that hypotenuse AC = 2BC.
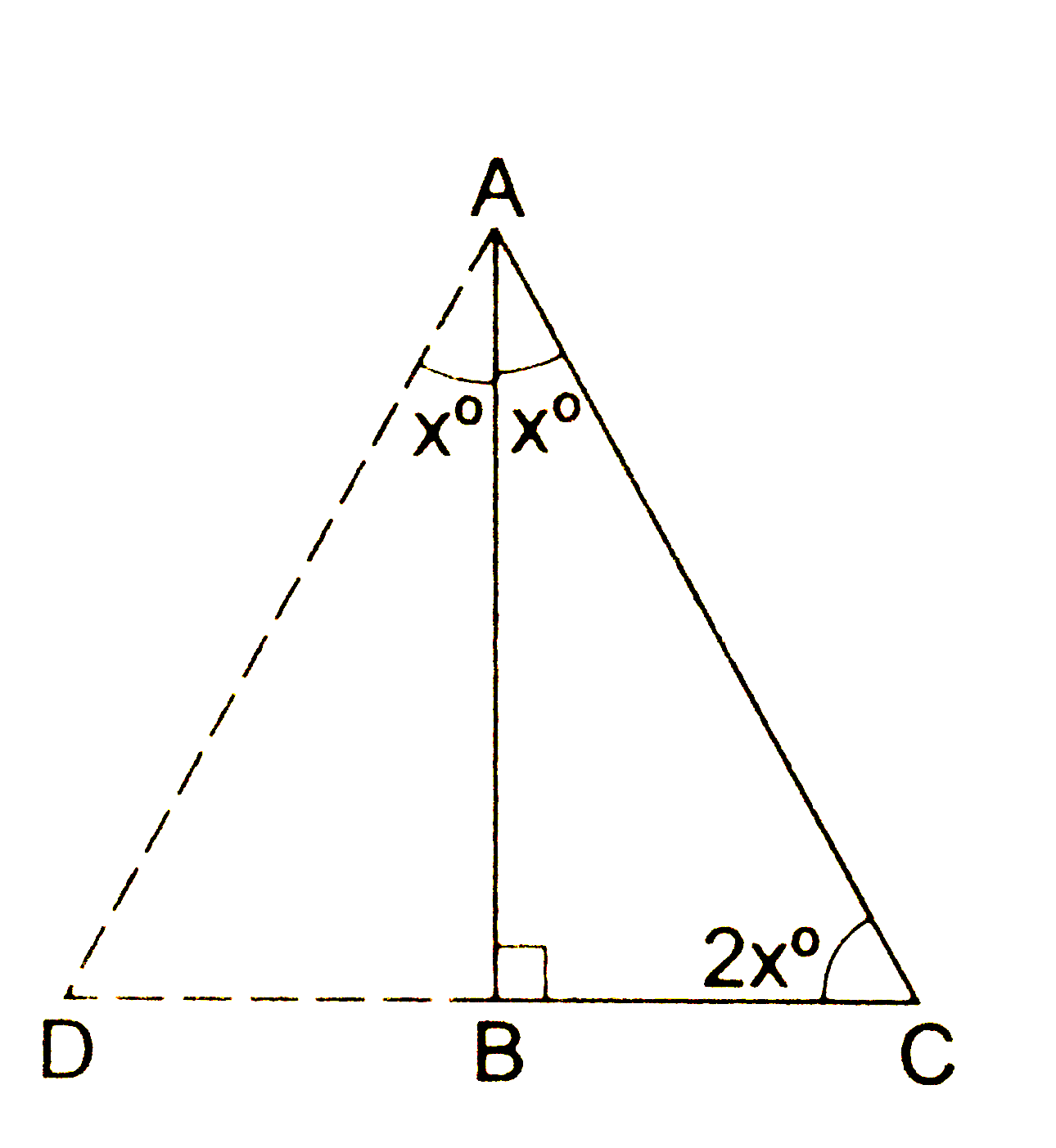 View Solution
View SolutionIf the perimeter of a right angled isosceles triangle is √2+1, then what is the length of the hypotenuse ?
View Solution

