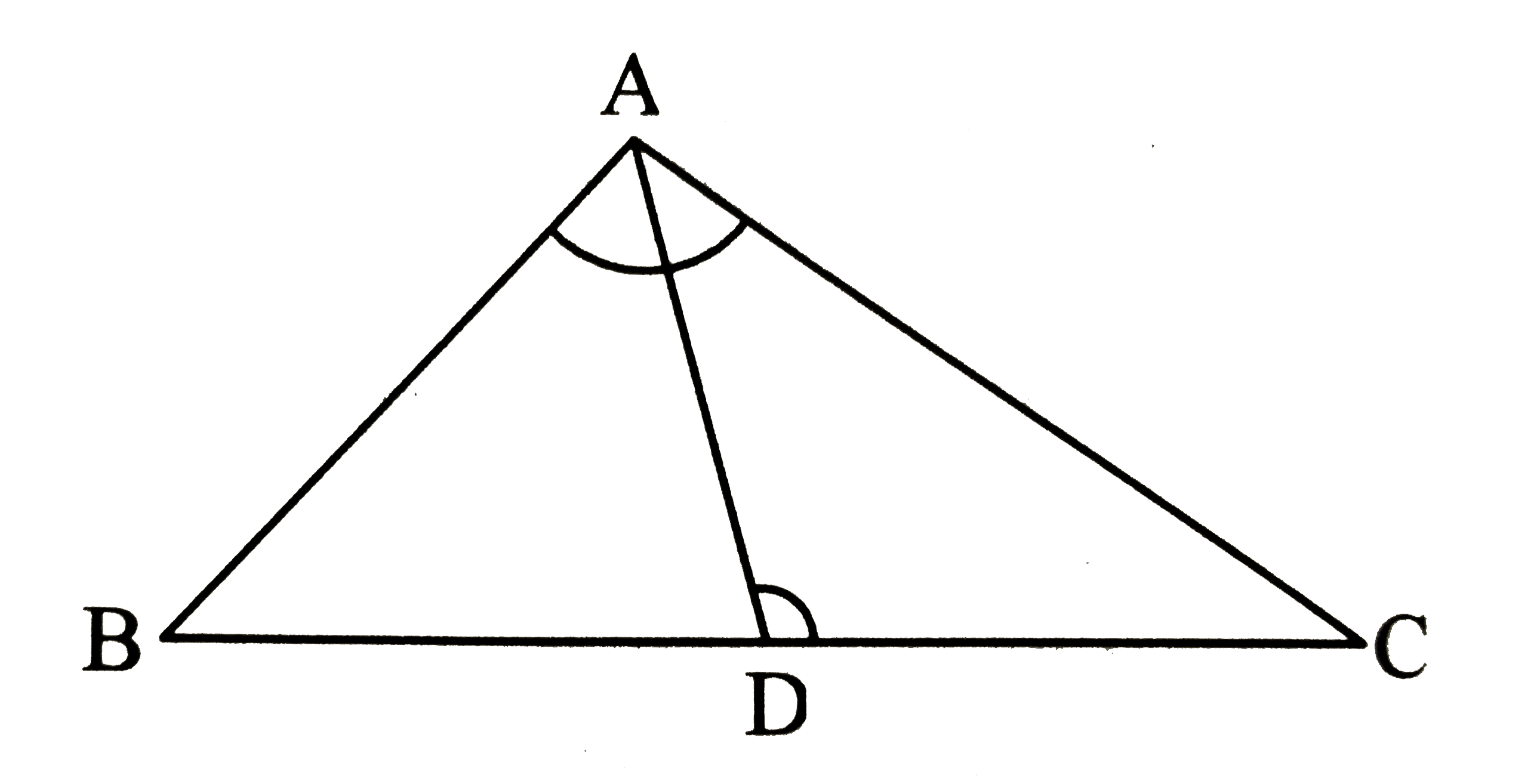
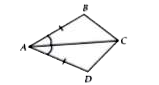
In the given figure, ΔABC is right angled at B such that ∠BCA=2∠BAC. Show that hypotenuse AC = 2BC.
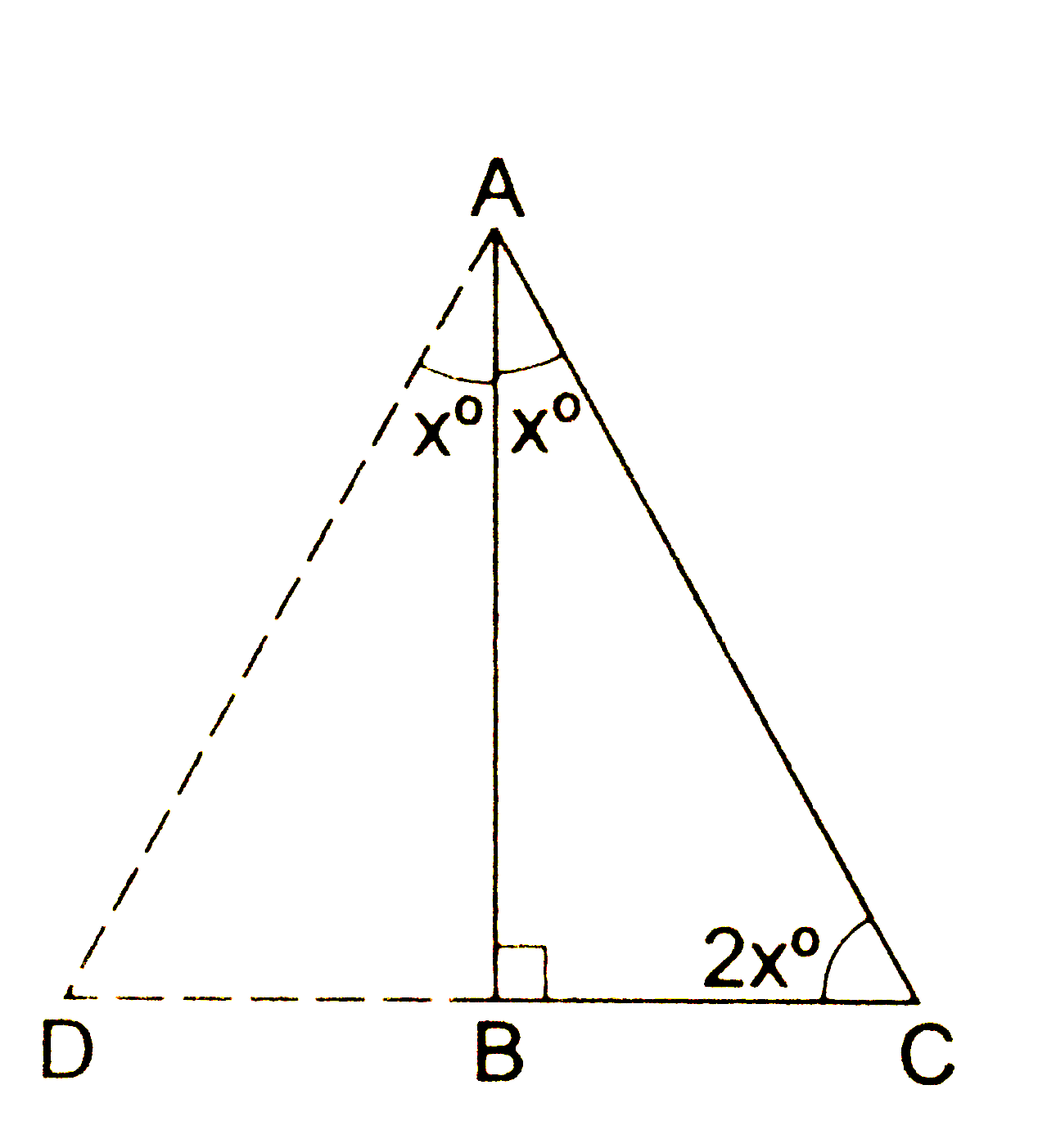
GIVEN A ΔABC in which ∠B=90∘and∠BCA=2∠BAC.
TO PROVE AC = 2BC.
CONSTRUCTION Produce CB to D such that BD = BC.
Join AD.
PROOF Let ∠BAC=x∘. Then, ∠BCA=2x∘.
In ΔABCandΔABD, we have
BC=BD (by construction)
AB=AB (common)
∠ABC=∠ABD=90∘
∴ ΔABC≅ΔABD (SAS-criteria)
∴ ∠CAB=∠DAB=x∘ ...(i) (c.p.c.t.).
and AC=AD ...(ii) (c.p.c.t.).
In ΔCAD, we have
∠CAD=∠CAB+∠DAB=(x∘+x∘)=2x∘.
∠ACD=∠ACB=2x∘.
But, we know that the sides opposite to equal angles are equal.
∴ ∠ACD=∠CAD⇒AD=CD. ...(iii)
From (ii) and (iii), we get
AC=CD⇒AC=2BC [∵CD=BC+BD=2BC].
Hence, AC=2BC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A27videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B16videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
 A2 cmB2√5 cmC5√2 cmD3√2 cm
A2 cmB2√5 cmC5√2 cmD3√2 cm - Question 2 - Select One
ΔABC is right angled at A. if AB = 24 mm and AC = 7 mm, then BC is
A20 mmB25 mmC30 mmD35 mm
In the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
 View Solution
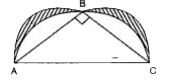
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
 View Solution
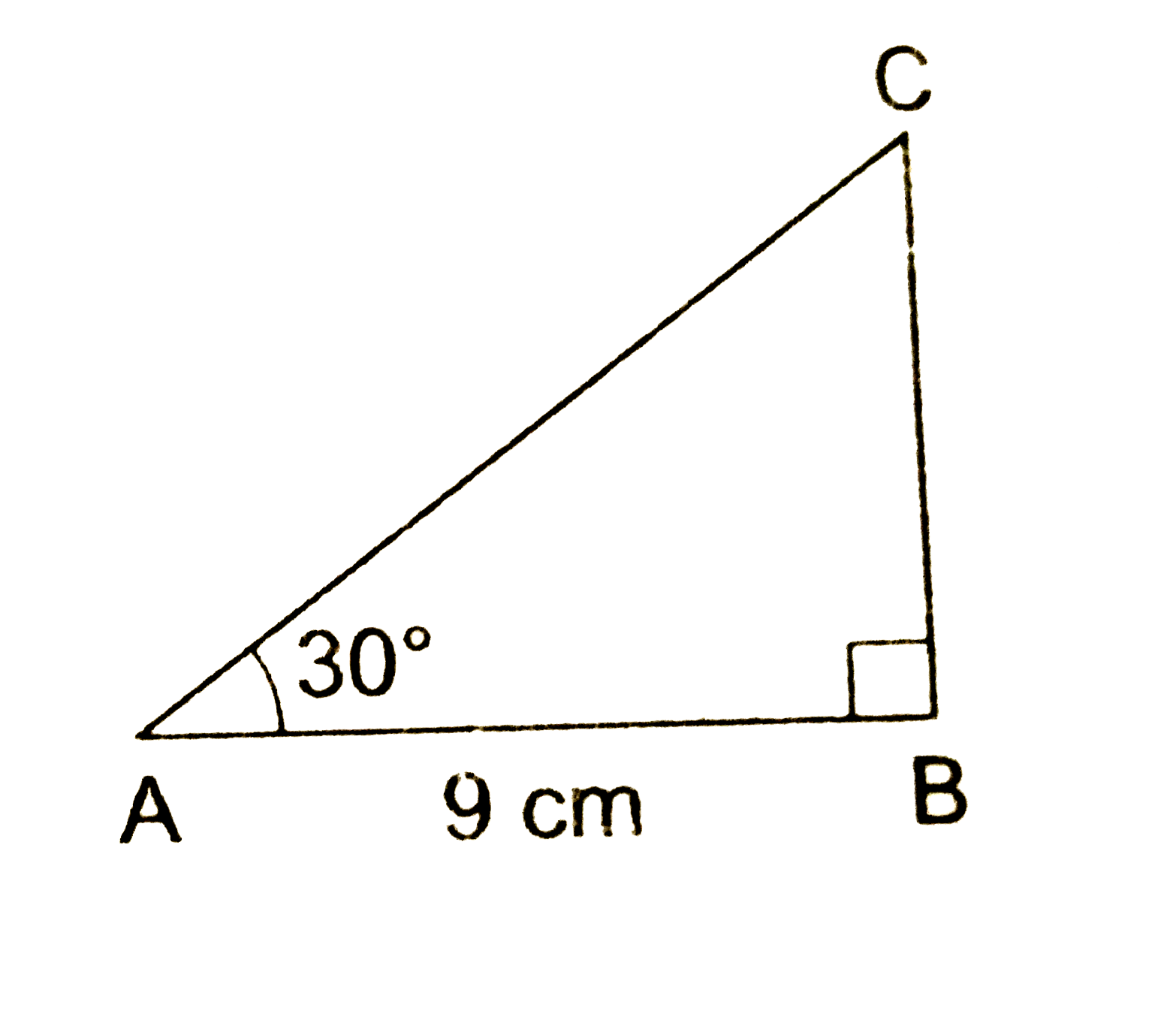
View SolutionIn the adjoining figure, ΔABC is right-angled at B. If ∠A=30∘ and AB=9cm, find (i)BC and (ii)AC.
 View Solution
View SolutionIn the adjoining figure , ΔABC is a right - angled triangle , right - angled at B. If ∠A=30∘andAC=8cm, Find (i)BC (ii)AB.
 View Solution
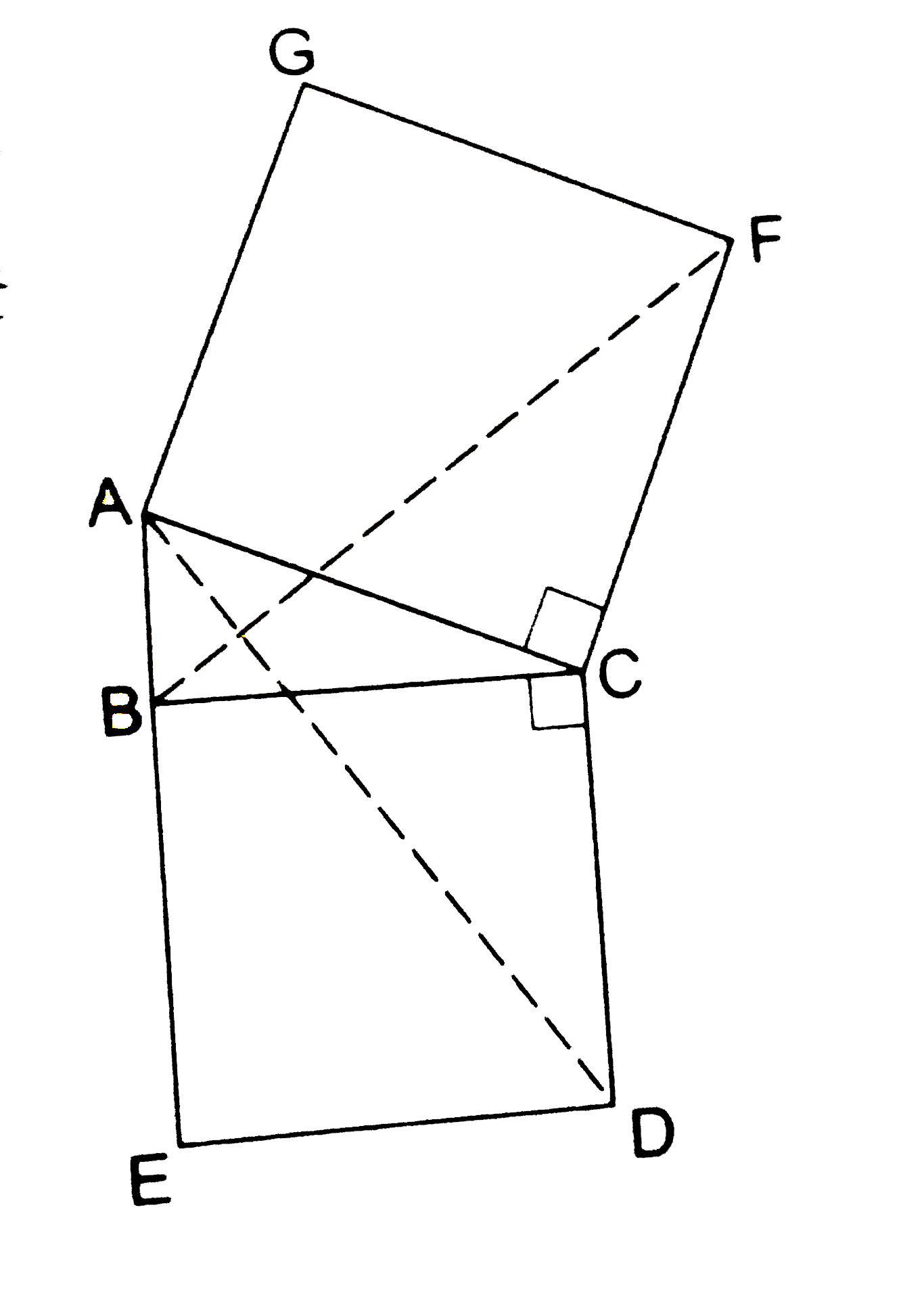
View SolutionIn the given figure, ABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = FB.
 View Solution
View SolutionIn the given figure, AB = AD and ∠BAC=∠DAC. Then
(iii) ∠BCA = ____.
 View Solution
View Solution