prove that the product of three consecutive positive integers is divisible by 6.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Let P(n)=n(n+1)(n+2) , where n is a positive integer
Step I For n=1,
P(1)=1(1+1)(1+2)=1.2.3=6, which is divisible by 6.
Therefore , the result is true for n=1.
Step II Let us assume that the result in true for n=k, where k is a positive integer
Then , P(k)=k(k+1)(k+2) is divisible by 6.
⇒P(k)=6r, where r is an integer .
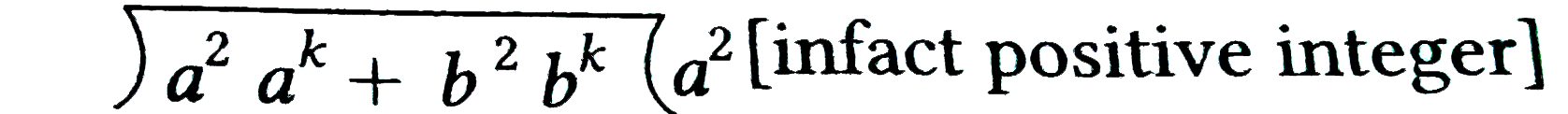
ocr_image
Step III For n=k+1, where k is a positive integer .
P(k+1)=(k+1)(k+1+1)(k+2+1)
=(k+1)(k+2)(k+3)
Now , P(k+1)−P(k)=(k+1)(k+2)(k+3)−k(k+1)(k+2)
=(k+1)(k+2)(k+3−k)
=3(k+1)(k+2)
⇒P(k+1)=P(k)+3(k+1)(k+2)
But we know that , P(k) is divisible by 6. Also , 39k+1)(k+2) is divisible by 6 for all positive integer. This shows that the result is true for n=k+1. Hence , by the principle of mathematical induction , the result is true for all positive integer.

Updated on:21/07/2023
|
Class 12MATHSMATHEMATICAL INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Statement-1: The smallest positive integer n such that n! can be expressed as a product of n-3 consecutive integers, is 6.
    Statement-2: Product of three consecutive integers is divisible by 6.

    AStatement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-1
    BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1
    CStatement-1 is true, statement-2 is false
    DStatement-1 is false, statement-2 is true

  • The sum of the cubes of three consecutive integers is divisible by

    A36
    B18
    C12
    D9