if a,b,c,d,e and f are six real numbers such that a+b+c=d+e+f a2+b2+c2=d2+e2+f2 and a3+b3+c3=d3+e3+f3 , prove by mathematical induction that an+bn+cn=dn+en+fn∀n∈N.
Let P(n):an+b2+cn=dn+en+fn,∀n∈N ..(i)
where a+b+c+d=e+ ...(ii)
a2+b2+c=d2+e2+f ....(iii)
and a2+b3+c3=d3+e2+3 ...(iv)
Step I from n from Eq. (i) we get
P(1):a+b+c=d+e+f [ given]
Hence the result is true for n 1
Also, for n=2 from Eq(i), we get
P(2):a2+b2+c2=d2+e3+f3 [ given]
Hennce the result true or n=3
Therefore, P(1) , P(2) and P (3) are true.
Step II Assume that P(k−2),P(k−1)andP(k) are true, then
P(k−2),ak−2+bk−2=dk−2+ek−2+f)k−2) ...(v)
p(k−1):a−1+bk−1+ck−1=dk−1+ek−1+fk−1 ....(vi)
and P(k):ak+bk+ck=dk+ek+fk m ...(vii)
Step III for xn=k+1 we shall to prove that
P(k+1):ak+1+bk+1=dk+1+ek+1+fk+1
LHS =ak+1+bk+1+ck+1
=(ak+bk(a+b+c)−(ak−1+bk−1+ck−1)
(ab+bc+ca)+abc(ak−2+bk−2+bk−2+ck−2)
=(dk+ef+fk)(d+e+f)−(dk−1+ek−1+ck−2)
(de+ef+fd)+def(dk−2+ek−2+fk−2)
[ using Eqs. (ii), (iii), (iv), (v), (vi), (vii)]
∴(a+b+c)2=(d+e+f)2
⇒a2+b2+c2+2(ab+bc+ca)
=d2+e2+f2+2(de+ef+fd)
⇒ab+bc+ca=de+ef+fd
[∴a2+b2+c2=d2+e2+f2]
and a3+b3+c3−3abc
(=d+e+f)(d2+e2+f2−de−ef−fd)
=d3+e3+f3−edf
⇒abc=def[∴a3+b3+c3=d3+e3+f3)
=dk+1+ek+1+fk−1=RHS
This shows that result is true for n=k+1. Hence by second perincipal of mathmatical inducition, the result is true for all n∈N.
Topper's Solved these Questions
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
Similar Questions
Knowledge Check
If ab=cd=ef=4, then
m2a+n2c+p2em2b+n2d+p2f=?A1B4C8D16
Let A and B be two sets such that n(A)=5 and n(B)=2, if a, b, c, d, e are distinct and (a,2), (b,3), (c,2), (d,3), (e,2) are in A×B , find A and B.
View SolutionThe AD,BEandCF are the medians of a cABC, then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionThe AD,BEandCF are the medians of a cABC, then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionLet A and B be two sets such that n(A)=5 and n(B)=2, if a, b, c, d, e are distinct and (a,2), (b,3), (c,2), (d,3), (e,2) are in A×B , find A and B.
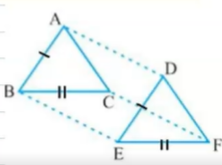
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AECF is a parallelogram whose area is one third of the area of parallelogram ABCD.
View SolutionIf n+1C3=2. nC2 then= 3 b. 4 c. 6 d. 5
View Solution
