If ABCDEF is a regular hexagon then −−→AD+−−→EB+−−→FC equals :
A
0
B
2AB
C
3AB
D
4AB
Video Solution
Text Solution
The correct Answer is:D
A regular hexagon ABCDEF.
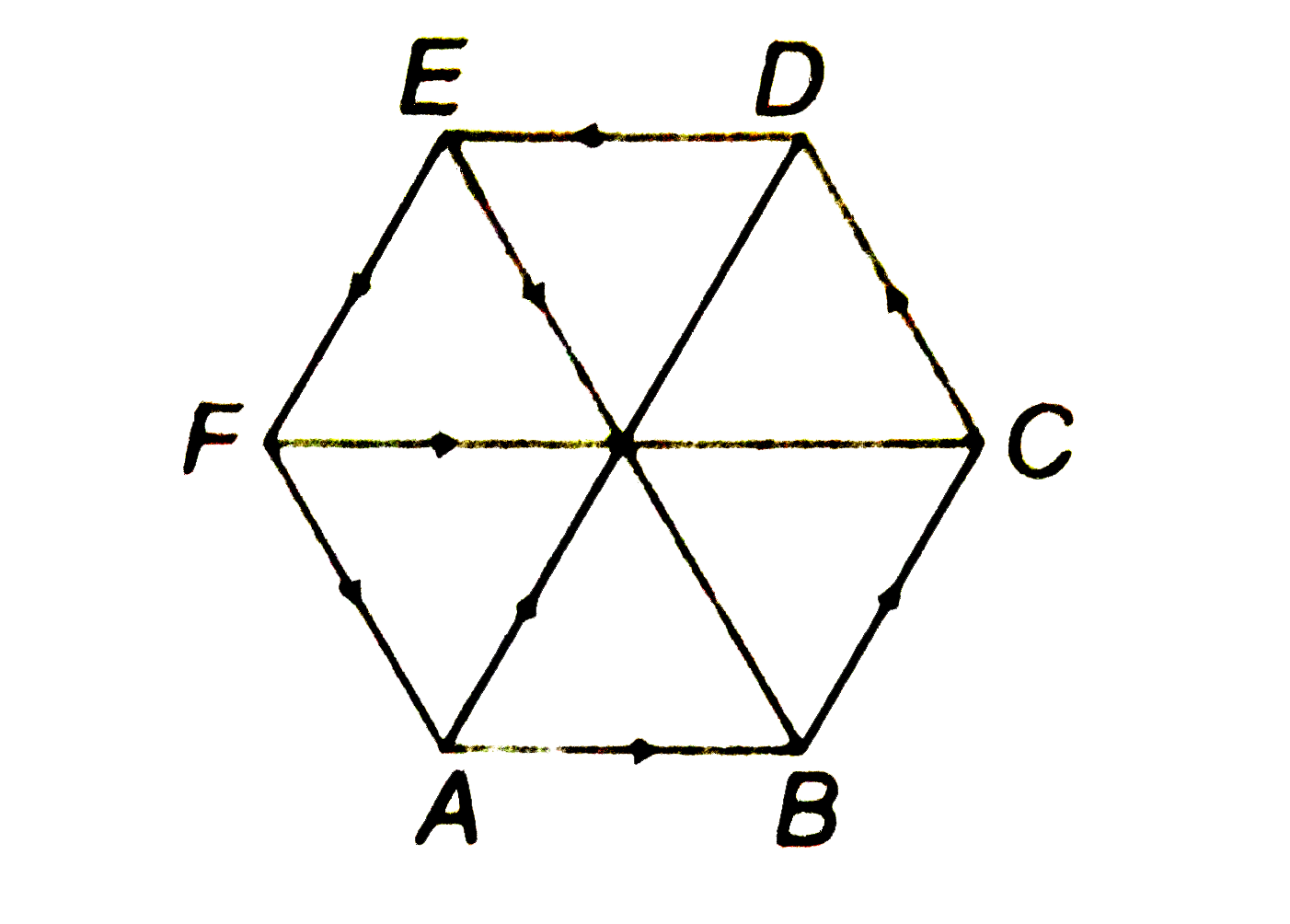
We know from the hexagon that AD is parallel to BC orr AD=2BC is parallel to FA or EB=2FA and FC is parallel to AB or FC=2AB.
Thus, AD+EB+FC=2BC+2FA+2AB
=2(FA+AB+BC)=2(FC)=2(2AB)=4AB.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)3videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 311videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)19videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals
A2A→BB→0C3A→BD4A→B - Question 2 - Select One
If ABCDEF is regular hexagon, then AD+EB+FC is equal to
A0B2ABC3ABD4AB - Question 3 - Select One
If ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
ABCDEF is a regular hexagon. Show that :
−−→OA+−−→OB+−−→OC+−−→OD+−−→OE+−−→OF=→0View SolutionIn Fig. ABCDEF is a ragular hexagon. Prove that
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=6−−→AO.View SolutionAssertion ABCDEF is a regular hexagon and −−→AB=→a,−−→BC=→band−−→CD=→c,then−−→EA is equal to −(→b+→c), Reason: −−→AE=−−→BD=−−→BC+−−→CD (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionIf ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
View Solution

