Ac227 has a half− life of 22.0 years with respect to one leading . To Th227 and the other to Fr227. The percentage yields of these two daughter nuclides are 2.0 and 98.0, respectively . What are the decay constants (λ) for each of the separate paths ?
For the radioactive decay of A into B and C by two parallel paths
So, −d[A]dt=λN....(i)
+d[B]dt=λ1N.....(ii)
+d[C]dt=λ2N....(iii)
where λ,λ1,and λ2 are radioactive decay constants, respectively, and N is the number of atoms of A at any given time.
Thus, +d[A]dt=d[B]dt+d[C]dt
∴λN=λ1N+λ2N
∴λ=λ1+λ2N
From eqs. (ii) and (iii), we get
d[B]d[C]=λ1λ2
On integration ,we get
[B][C]=λ1λ2
For decay of Ac227 into Th227 and Fr223 , on the basis of given data
λ1λ2=2.098.0....(iv)
and λ=0.693t1/2=0.69322=0.0315year−1 ltbr> So,0.0315=λ1+λ2...(v)
On solving Eqs. (iv) and (v), we get
λ1=6.3×10−4year−1
and λ2=0.03087year−1

Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRYCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Fill In The Blanks
5 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRYCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRYCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
Ac227 has a half life of 22 year . The decay follows two parallel paths, one leading the Th227 and the other leading to Fr223. The precentage yields of these two daughters nucleoids are 2% and 98 % respectively. What is the rate constant in yr−1, for each of the separate paths ?
View Solution227Ac has a half-life of 21.8 years with respect to radioactive decay. The decay follows two parallel paths, one leading to 227Th and the other leading to 223Fr. The percentage yields of these two daughter nuclides are 1.2% and 98.8% respectively. what is the rate constant in y−1, for each of the separate paths?
View Solution
Knowledge Check
227Ac has a half-life of 22 years with respect to radioactive decay. The decay follows two prallel paths : 227Ac→227Th and 227Ac→223Fr. If the percentage of the two daughter nuclides are 2.0 and 98.0, respectively, the decay constant (in year−1) for 227Ac→227Th path is closest to
A6.3×10−2B6.3×10−3C6.3×10−1D6.3×10−4Ac227 has a half-life of 22 years . The decays follows two parallel paths
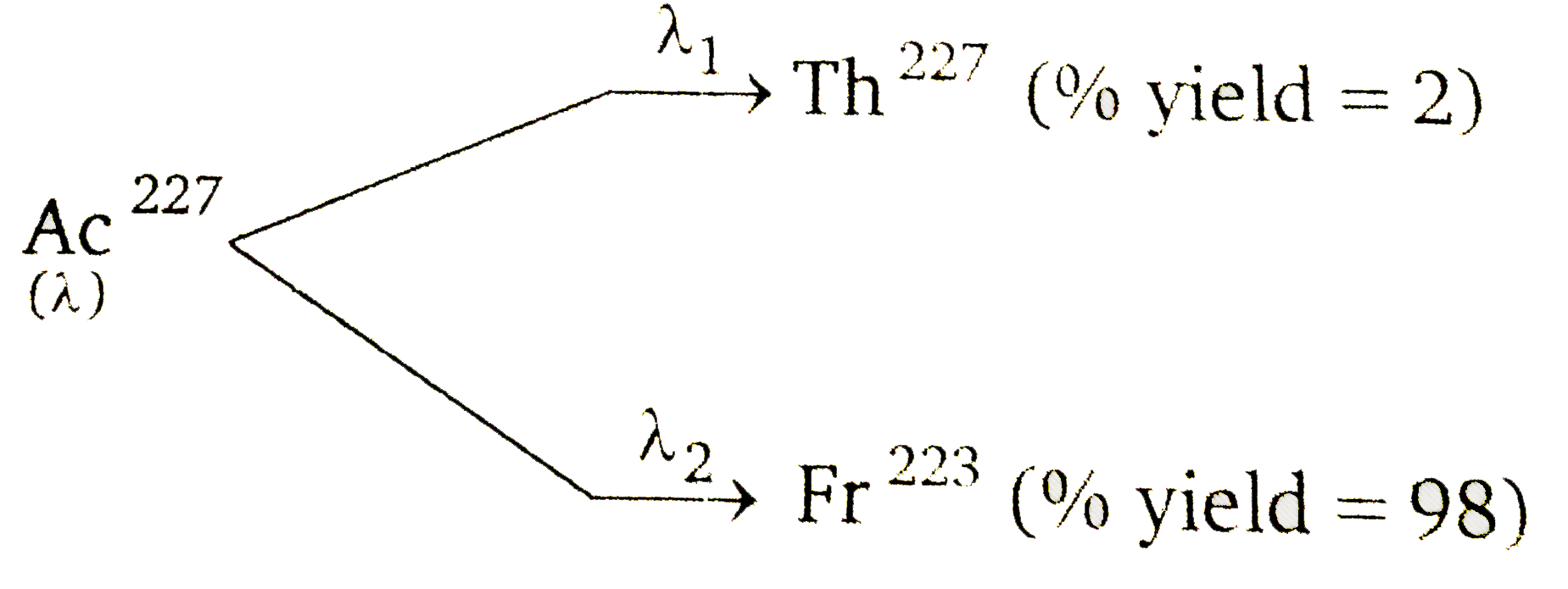
What are the decay constant (λ) for Th and Fr respectively ?A0.03087,0.00063B0.00063,0.03087C0.02,0.98DNone of theseThe half-life of 2 sample are 0.1 and 0.4 seconds. Their respctive concentration are 200 and 50 respectively. What is the order of the reaction
A0B2C1D4
.227Ac has a half-line of 22 year with respect to radiioactive decay. The decay follows two parallel paths, one leading to .227Th and the other leading to .223Fr. The percentage yiedls of these two daughter nuclides are 2% and 98.0% respectovely. What is the rate constant in year−1, for each of the separate paths?
View SolutionAc227 has a half-life of 22 years . The decays follows two parallel paths
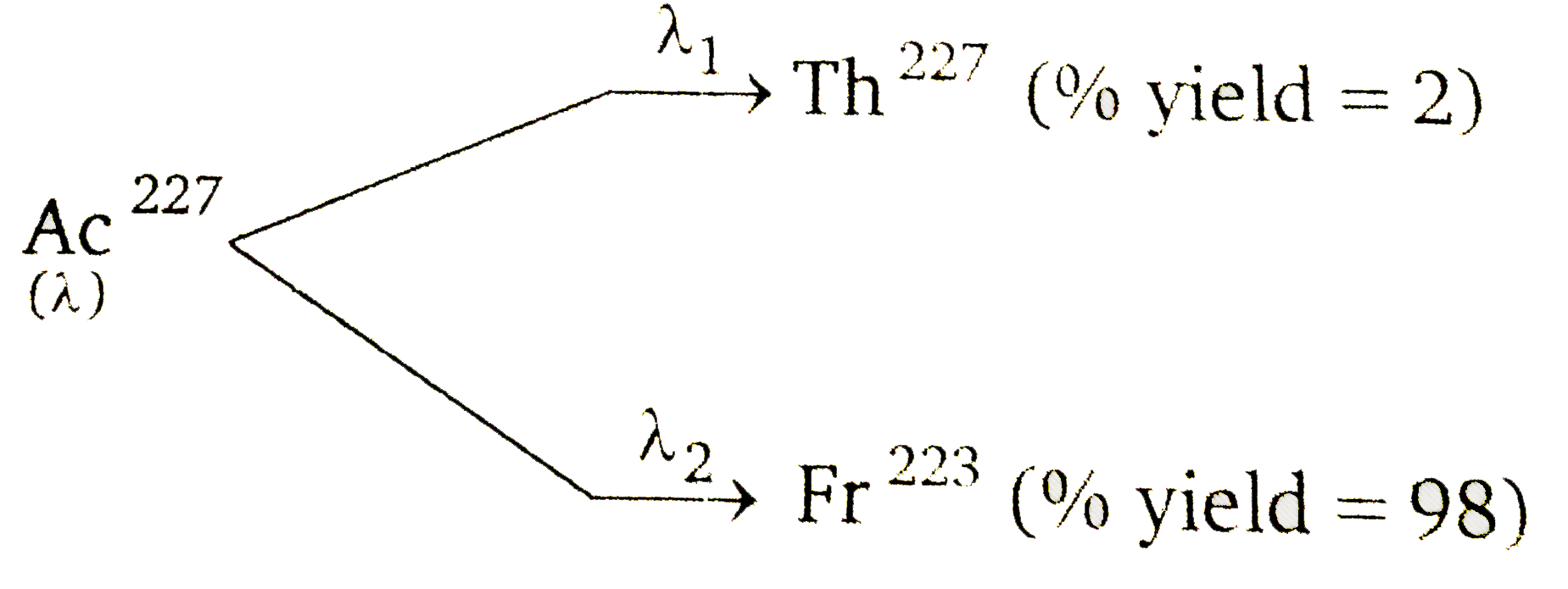
What are the decay constant (λ) for Th and Fr respectively ?
View SolutionThe half-life of 2 sample are 0.1 and 0.4 seconds. Their respctive concentration are 200 and 50 respectively. What is the order of the reaction
View SolutionThe half-life of 2 sample are 0.1 and 0.4 seconds. Their respctive concentration are 200 and 50 respectively. What is the order of the reaction
View SolutionAnalysis shows that nickel has the formula Ni0.98O. The percentage of Ni present as Ni2+andNi3+, respectively, will be
View Solution
