.227Ac has a half-line of 22 year with respect to radiioactive decay. The decay follows two parallel paths, one leading to .227Th and the other leading to .223Fr. The percentage yiedls of these two daughter nuclides are 2% and 98.0% respectovely. What is the rate constant in year−1, for each of the separate paths?
We know,
λav=0.69322=3.15×10−2year−1
For the decay involving two parallel paths,

We have λAc=λTh path+λFr path
∴ΛAc×Fraction of Th=λTh path ....(1)
λAC×Fraction of Fr=λFr path .....(2)
or λAC×(1−Fraction of Th)=λFr path .....(3)
Thus by eqs. (1) and (3) we get
λAC=λTh path+λFr path
Thus by eqs. (1) and (3) we get
λAC=λTh path+λFr path
Thus, Fractionlal yield of Th=λTh pathλAc path
or λTh path=3.15×10−2×2100
=6.30×10−4yr−1
Also Fractional yeild of Fr=λFr pathλAcpath
∴λFr=3.15×10−2×98100=3.087×10−2yr−1
Topper's Solved these Questions
- RADIO ACTIVITYBOOK - P BAHADURCHAPTER - RADIO ACTIVITYEXERCISE - Exercies 3A
92 Videos
- RADIO ACTIVITYBOOK - P BAHADURCHAPTER - RADIO ACTIVITYEXERCISE - Exercies 3B
13 Videos
- RADIO ACTIVITYBOOK - P BAHADURCHAPTER - RADIO ACTIVITYEXERCISE - Exercies 9
99 Videos
- MOLE AND EQUIVALENT CONCEPTBOOK - P BAHADURCHAPTER - MOLE AND EQUIVALENT CONCEPTEXERCISE - Exercise 9 Advanced numerical problems
61 Videos
- REDOX REACTIONSBOOK - P BAHADURCHAPTER - REDOX REACTIONSEXERCISE - Exercise(8) Statement:Explanation type problems
19 Videos
Similar Questions
227Ac has a half-life of 21.8 years with respect to radioactive decay. The decay follows two parallel paths, one leading to 227Th and the other leading to 223Fr. The percentage yields of these two daughter nuclides are 1.2% and 98.8% respectively. what is the rate constant in y−1, for each of the separate paths?
View SolutionAc227 has a half life of 22 year . The decay follows two parallel paths, one leading the Th227 and the other leading to Fr223. The precentage yields of these two daughters nucleoids are 2% and 98 % respectively. What is the rate constant in yr−1, for each of the separate paths ?
View Solution
Knowledge Check
227Ac has a half-life of 22 years with respect to radioactive decay. The decay follows two prallel paths : 227Ac→227Th and 227Ac→223Fr. If the percentage of the two daughter nuclides are 2.0 and 98.0, respectively, the decay constant (in year−1) for 227Ac→227Th path is closest to
A6.3×10−2B6.3×10−3C6.3×10−1D6.3×10−4Ac227 has a half-life of 22 years . The decays follows two parallel paths
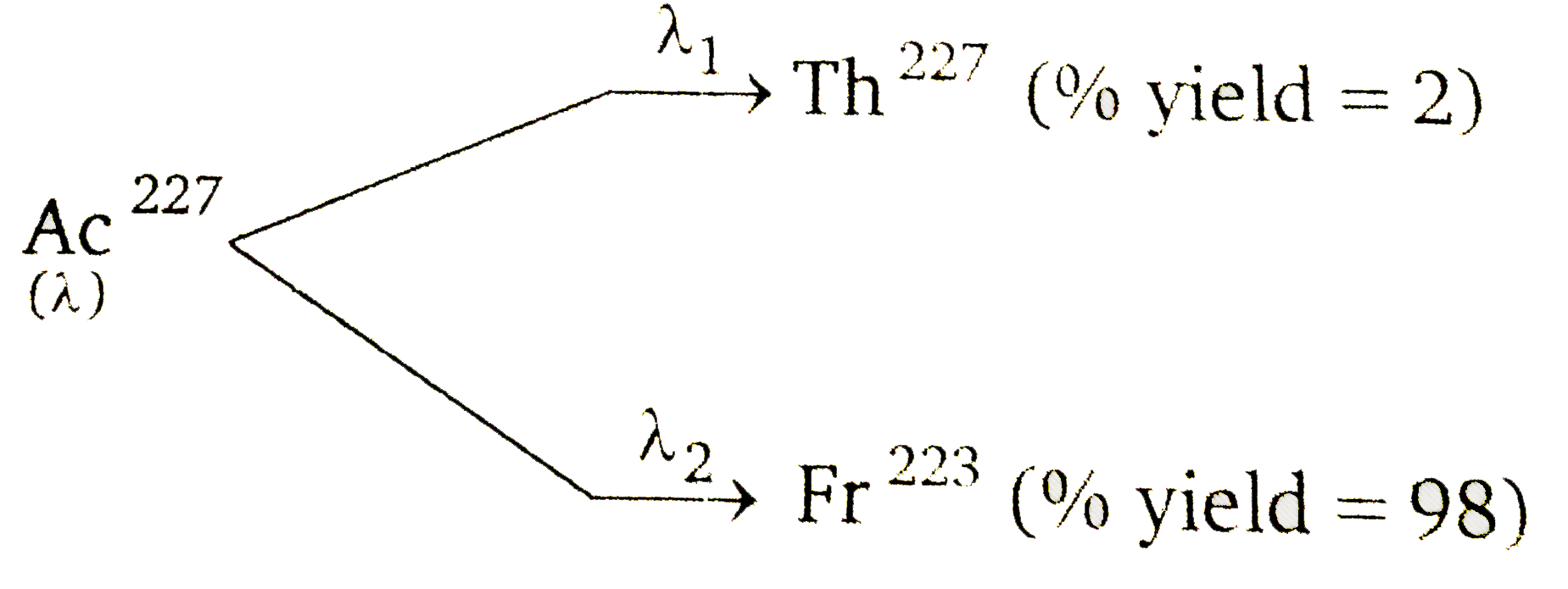
What are the decay constant (λ) for Th and Fr respectively ?A0.03087,0.00063B0.00063,0.03087C0.02,0.98DNone of theseIf half lives of a radioactive element, undergoing parallel path α−decay and α−decay are 4 years and 12 years respectively, then percentage of element that remains after 12 years will be:
A0.5B0.125C0.0625D0.25
Ac227 has a half− life of 22.0 years with respect to one leading . To Th227 and the other to Fr227. The percentage yields of these two daughter nuclides are 2.0 and 98.0, respectively . What are the decay constants (λ) for each of the separate paths ?
View SolutionAc227 has a half− life of 22.0 years with respect to one leading . To Th227 and the other to Fr227. The percentage yields of these two daughter nuclides are 2.0 and 98.0, respectively . What are the decay constants (λ) for each of the separate paths ?
View SolutionAc227 has a half-life of 22 years . The decays follows two parallel paths
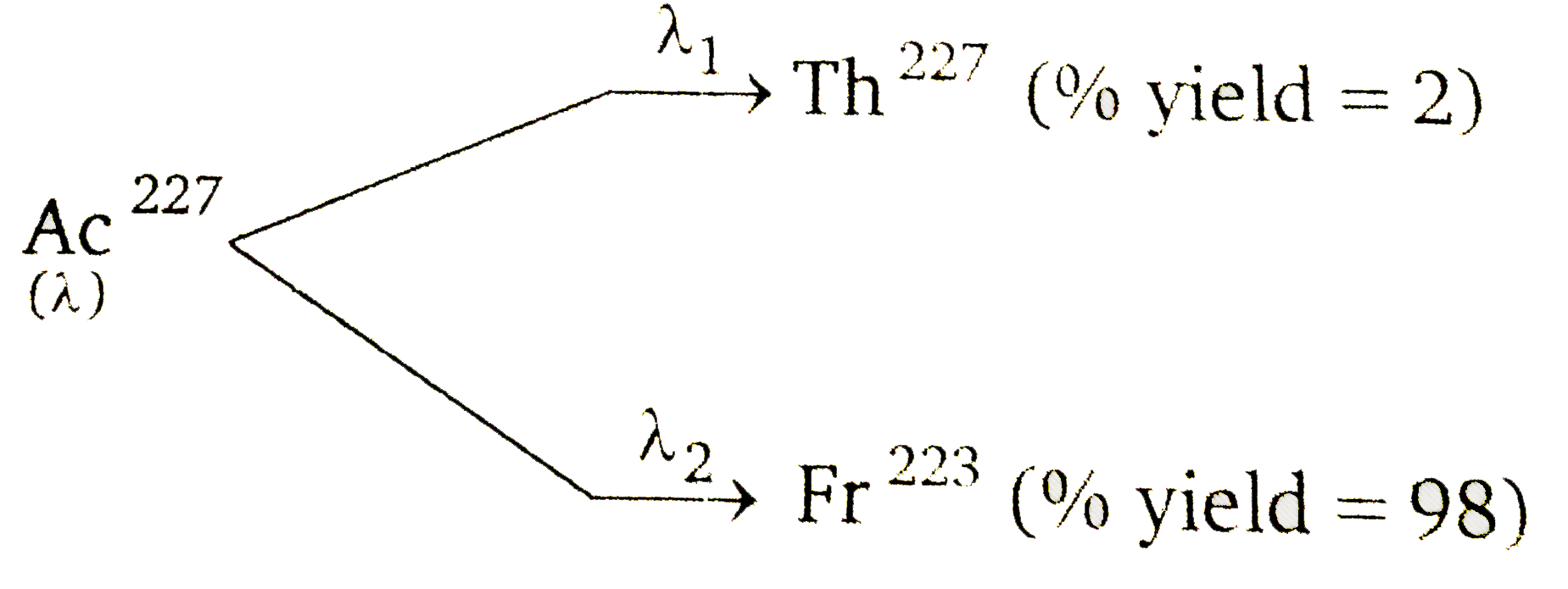
What are the decay constant (λ) for Th and Fr respectively ?
View SolutionTrans 1,2-dideuterocyclopropane (A) undergoes a first order decompoistion. The observed rate constant at a certain temperature, measured in terms of disapperance of A was 1.52×10−4s−1. The analyiss of Products shwoed that the reaction followed two parallel paths, one leading to dideuteropropane (B) and the other to cis-1,2-dideuterocyclopropane (c). (B) was found to constitute 11.2% of the reaction Product, independently of the extent of reaction. What is the order of reaction for each path and what is the value of the rate constant for the formation of each of the Products ?
View SolutionHalf-life of 210Pb is 22 years. 2gram of lead is allowed decay for 11 years. (a) How much lead is left ?and (b) What is the percentage decay ?
View Solution
