Let the minimum external work done in shifted a particle form centre of earth to earth's surface be W1 and that form surface of earth to infinity be W2 . Then W1W2 is equl to
A
1:1
B
1:2
C
2:1
D
1:3
Video Solution
Text Solution
The correct Answer is:B
W1W1=−GMR−(32GMR)0−(−GMR)=12
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The work done liftting a particle of mass 'm' from the centre of the earth to the surface of the earth is
A−mgRB12mgRCZeroDmgR - Question 2 - Select One
Assertion : Let W1 be the work done in taking away a satellite from the surface of earth to its orbit and then W2 the work done in rotating the satellite in circular orbit there. Then, W1=W2
Reason : W2=GMm4RAIf both Assertin and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is true - Question 3 - Select One
The work done by an external agent to shift a point mass from infinity to the centre of the earth is W. Then choose the correct relation.
AW=0BW>0CW<0DW≤0
The work done in moving a particle in the gravitational field of earth from point A to point B along three different paths 1,2 and 3 are W1,W2 and W3 respectively , then
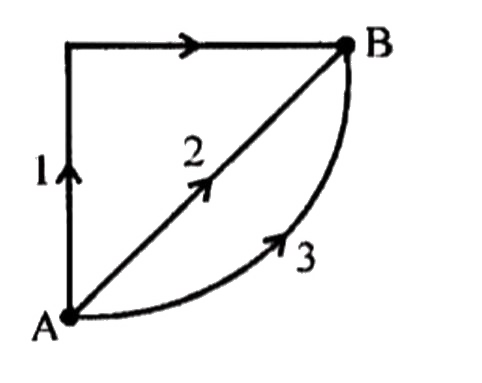 View Solution
View SolutionTwo weights W1 and W2 in equilibrium and at rest, are suspended as shown in figure. Then the ratio W1W2 is :
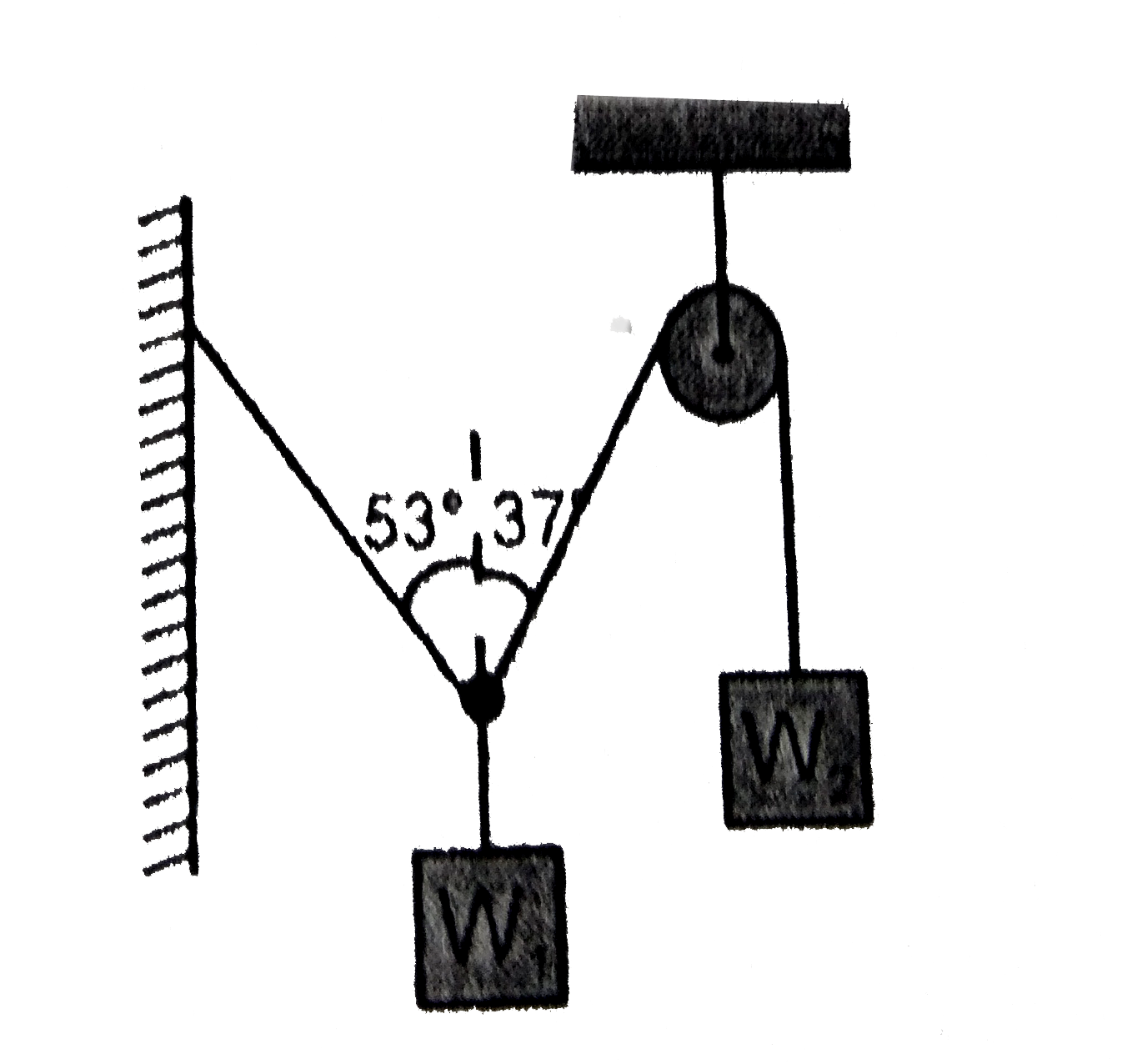 View Solution
View SolutionWork done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
View SolutionA man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is (R is Radius of the earth )
View SolutionThe weight of a body on the surface of earth is W When the density of the body is doubled by keeping its radius constant, its weight on the surface of the moon is found to beWm then WmWe=______ge=6gm
View Solution

