Two rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
80∘C
64∘C
20∘C
16∘C
The correct Answer is:D
To solve the problem, we need to find the temperature at the junction of two rods made of copper and brass. We will use the concept of thermal conductivity and the steady-state condition where the heat flow through both rods is equal.
1. Identify Given Data:
- Let the thermal conductivity of brass be KB.
- Then, the thermal conductivity of copper will be KC=4KB.
- Temperature at the free end of copper rod, TC=0∘C.
- Temperature at the free end of brass rod, TB=80∘C.
- Let the temperature at the junction be T0.
2. Set Up Heat Current Equations:
- The heat current through the copper rod can be expressed as:
QC=KC⋅A⋅(T0−TC)L
- The heat current through the brass rod can be expressed as:
QB=KB⋅A⋅(TB−T0)L
- Here, A is the cross-sectional area, and L is the length of the rods.
3. Equate the Heat Currents:
- Since we are in steady state, the heat current through both rods must be equal:
QC=QB
- Substituting the expressions for QC and QB:
KC⋅A⋅(T0−0)L=KB⋅A⋅(80−T0)L
- We can cancel A and L from both sides:
KC⋅T0=KB⋅(80−T0)
4. Substitute KC=4KB:
- Replacing KC in the equation:
4KB⋅T0=KB⋅(80−T0)
- Dividing both sides by KB (assuming KB≠0):
4T0=80−T0
5. Solve for T0:
- Rearranging the equation gives:
4T0+T0=80
5T0=80
T0=805=16∘C
6. Conclusion:
- The temperature at the junction of the two rods is T0=16∘C.
- Let the thermal conductivity of brass be KB.
- Then, the thermal conductivity of copper will be KC=4KB.
- Temperature at the free end of copper rod, TC=0∘C.
- Temperature at the free end of brass rod, TB=80∘C.
- Let the temperature at the junction be T0.
- The heat current through the copper rod can be expressed as:
QC=KC⋅A⋅(T0−TC)L
- The heat current through the brass rod can be expressed as:
QB=KB⋅A⋅(TB−T0)L
- Here, A is the cross-sectional area, and L is the length of the rods.
- Since we are in steady state, the heat current through both rods must be equal:
QC=QB
- Substituting the expressions for QC and QB:
KC⋅A⋅(T0−0)L=KB⋅A⋅(80−T0)L
- We can cancel A and L from both sides:
KC⋅T0=KB⋅(80−T0)
- Replacing KC in the equation:
4KB⋅T0=KB⋅(80−T0)
- Dividing both sides by KB (assuming KB≠0):
4T0=80−T0
- Rearranging the equation gives:
4T0+T0=80
5T0=80
T0=805=16∘C
- The temperature at the junction of the two rods is T0=16∘C.
Topper's Solved these Questions
Similar Questions
The thermal conductivity of copper is four times that of brass. Two rods of copper and brass of same length and cross-section are joined end to end. The free end of copper rod is at 0∘C and that of brass rod at 100∘C. Calculate the temperature of junction at equilibrium. neglect radiation losses.
View SolutionThree rods of equal length and equal area of cross section are connected end to end in series. The open end of the first rod (from left) is at a temperature of 300∘C and that of the last rod is at 20∘C in steady state. If the thermal conductivities of rods from left to right are in the ratio of 1: 3: 4, then find the temperatures of both the junctions.
View Solution
Knowledge Check
- Question 1 - Select One
A large cylindrical rod of length L is made by joining two identical rods of copper and steel of length (L2) each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at 100∘C and that of steel at 0∘C then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
A90∘CB50∘CC10∘CD67∘C - Question 2 - Select One
Three metal rods made of copper, aluminium and brass, each 20cm long 4cm in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at 100 and 0∘C respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.
 A68∘C and 75∘CB75∘C and 68∘CC57∘C and 86∘CD86∘ and 57∘C
A68∘C and 75∘CB75∘C and 68∘CC57∘C and 86∘CD86∘ and 57∘C - Question 3 - Select One
Figure shows a copper rod joined to a steel rod. The rods have equal length and equal cross-sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C. Find the temperature θ at the junction of the rods. Conductivity of copper
=390W/m−∘C and that of steel =46W/m−∘C.
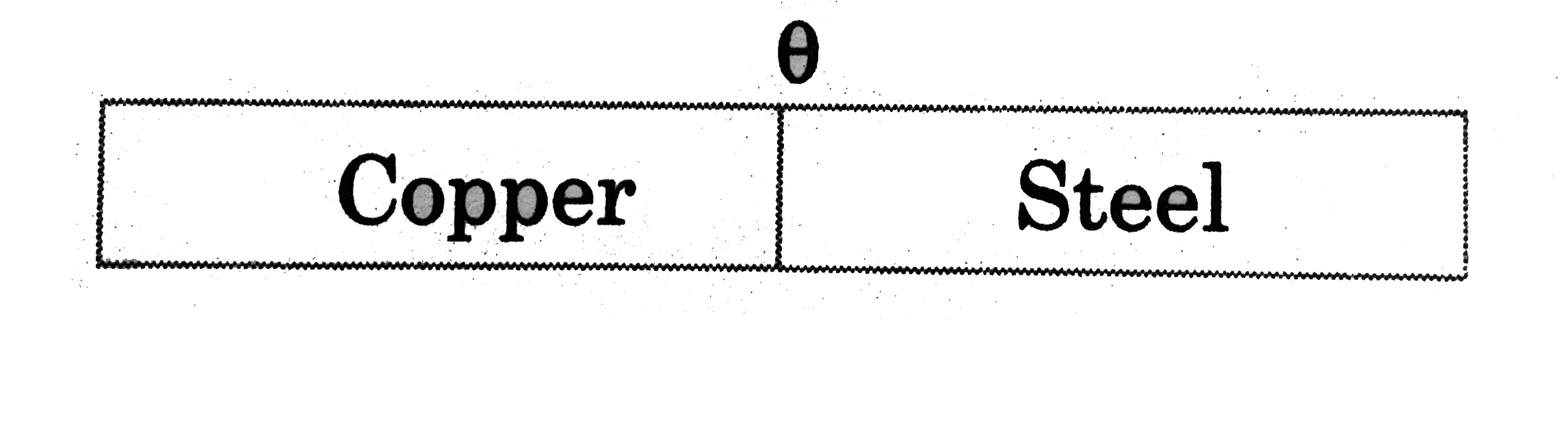 .A20.55∘CB30.55∘CC10.55∘CDNone of these
.A20.55∘CB30.55∘CC10.55∘CDNone of these
Three rods AB,BC and BD made of the same materical and having the same area of cross section have been joined as shown is the The ends A,C and D are held at temperatures 20∘C Cand 80∘C respectively If each rod is of same length then find the temperature at the junction B of the three rods
 .View Solution
.View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .
 View Solution
View SolutionA composite rod of uniform cross-section has copper and aluminium sections of the same length in good thermal contact. The ends of the rod, which is well-lagged, are maintained at 100∘C and at0∘C as shown in the diagram (Figure-4.33). The thermal conductivityof copper is twice that of aluminium.
Which one of the following graphs represents the variation of temperature T with x along the rod in the steady state ?
 View Solution
View SolutionA cylindrical steel rod of length 0.10 m and thermal conductivity 50W.m−1K−1 is welded end to end to copper rod of thermal conductivity 400W.m−1.K−1 and of the same area of cross section but 0.20 m long. The free end of the steel rod is maintained at 100∘C and that of the copper and at 0∘C. Assuming that the rods are perfectly insulated from the surrounding, the temperature at the junction of the two rods–
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View Solution

