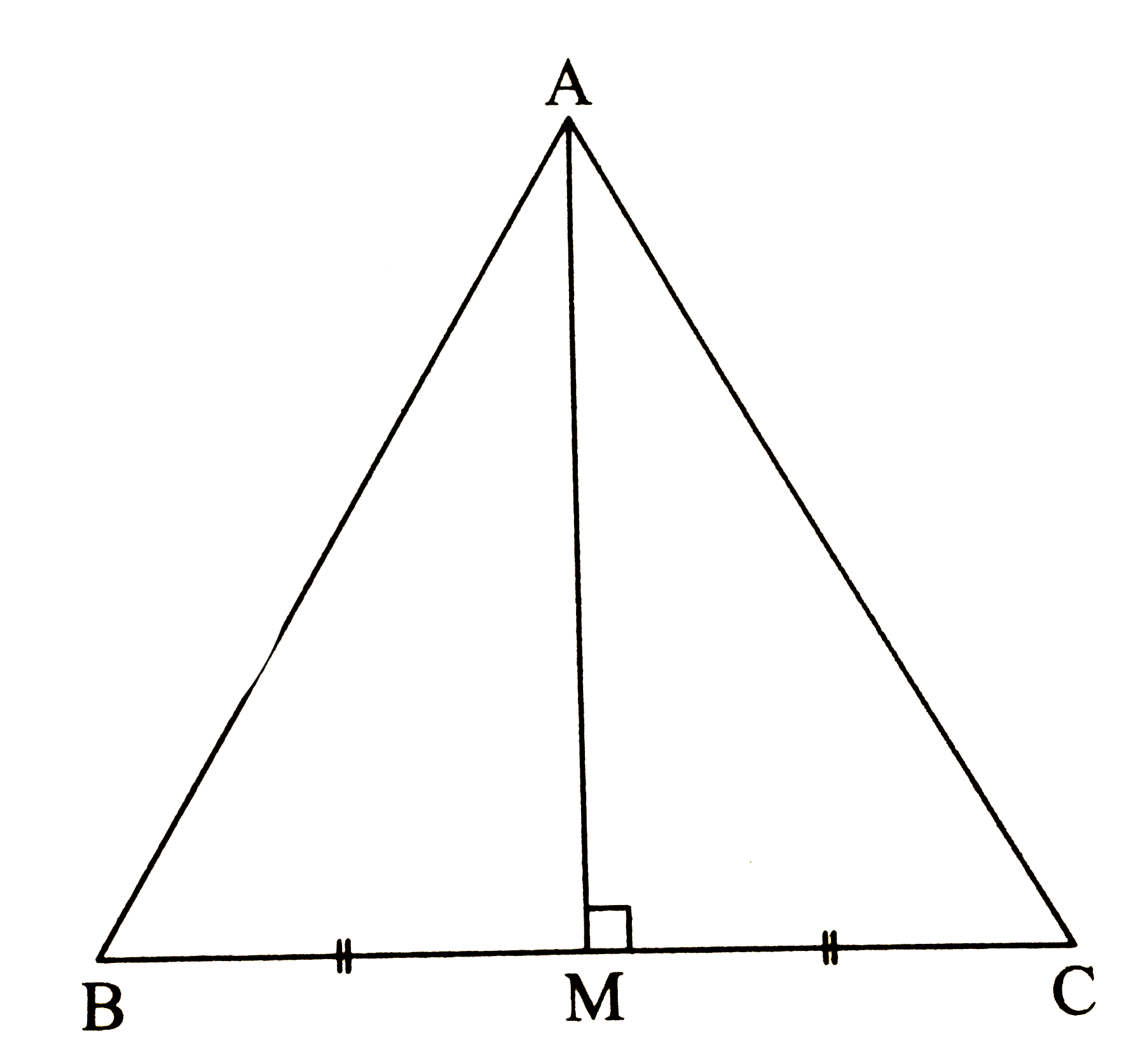
In if M is the midpiont of BC and seg AM seg BC, then prove that prove that
Video Solution
Text Solution
Proof Let's consider the case, where AM is not perpendicular to seb BC, then out of and , one is acute angle and other is obtuse angle.
Let's consider as an acute angle and as an obtus angle.
is an acute angled triangle,
by application of Pythagoras theorem, we get,
...(1)
is an obtuse angled triangle.
By application of Pythagoras theorem, we get ,
...(2)
But MC= BM ...(M is the midpoint of side BC ) ...(3)
Substituting (3) in (2), we get
..(4)
Adding (1) and (4) , we get ,
Let's consider the case, where seg seg BC
In ,
by Pythagoras theorem,.
...(5)
In ,
by Pythagoras theorem,
But MC = BM .....(M is the midpoint of side BC ) ...(7)
....[From (6) and ( 7) ] ....(8)
Adding (5) and (8), we get,
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - CIRCLE15videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - CIRCLE15videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS6videos
TRIGONOMETRY
Similar Questions
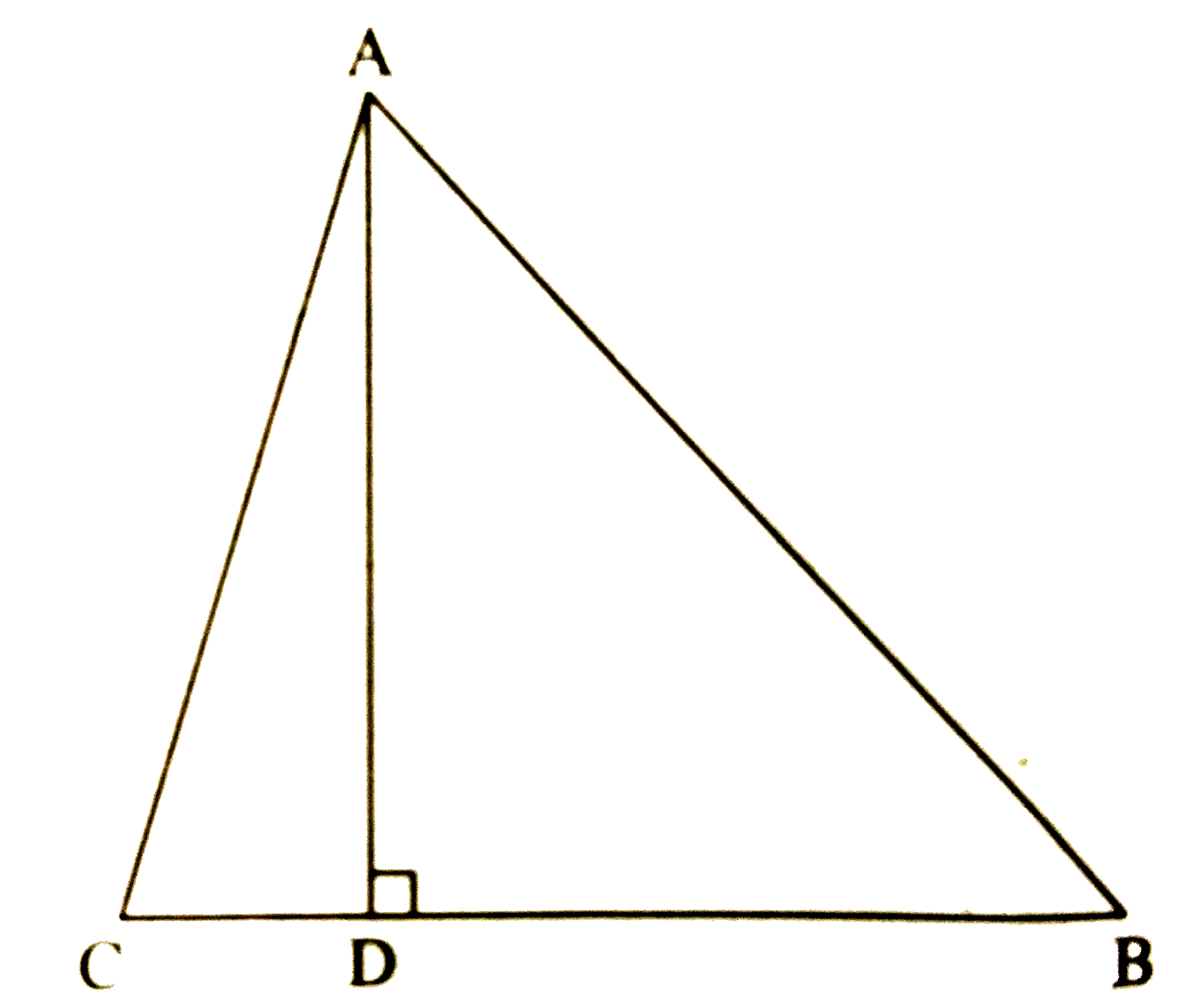
In ΔABC,
seg AD⊥ seg BC,
DB=3CD.
Prove that 2AB2=2AC2+BC2.
 View Solution
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
 View Solution
View SolutionPoint M is the mid point of seg AB and AB = 14 unit then AM =?
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
 View Solution
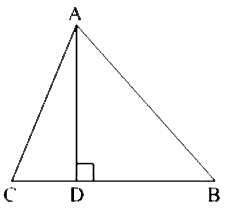
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionSee the given figure. In ΔABC, seg AD⊥ seg BC. Prove that: AB2+CD2=BD2+AC2
 View Solution
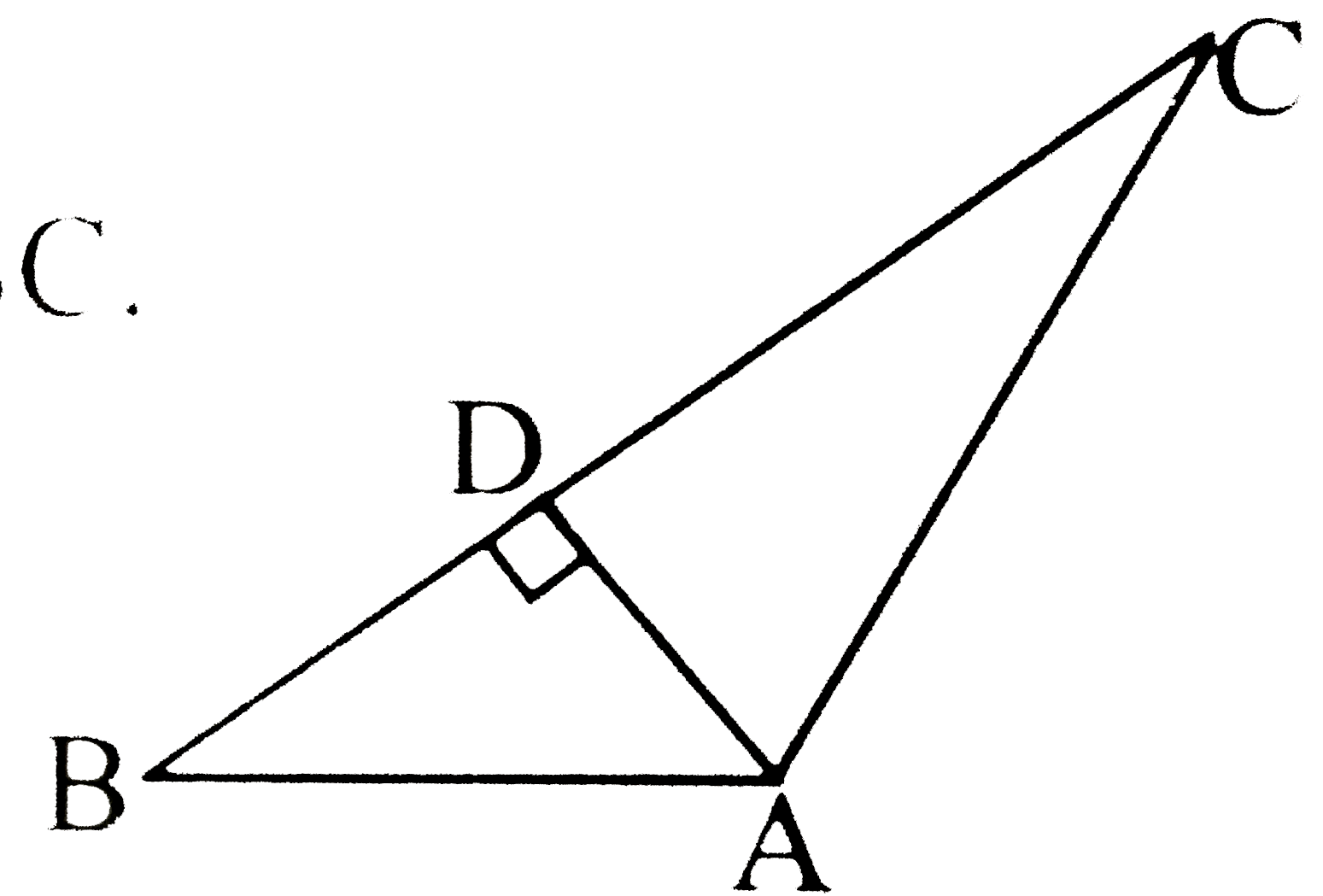
View SolutionIn the figure, seg AD⊥ side BC and B−D−C, then prove AB2−BD2=AC2−CD2.
 View Solution
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIf in ΔABC, seg AM is the median, AB2+AC2=410 and BC=12 then AM=?
View Solution

