In the figure, seg $A B ≅$ seg $A C$ , ray $C E$ bisects $∠ A C B$ , ray $B D$ bisects $∠ A B C$ . Prove that ray $E D ∣ ∣$ side $B C$ .

Video Solution

|

Answer

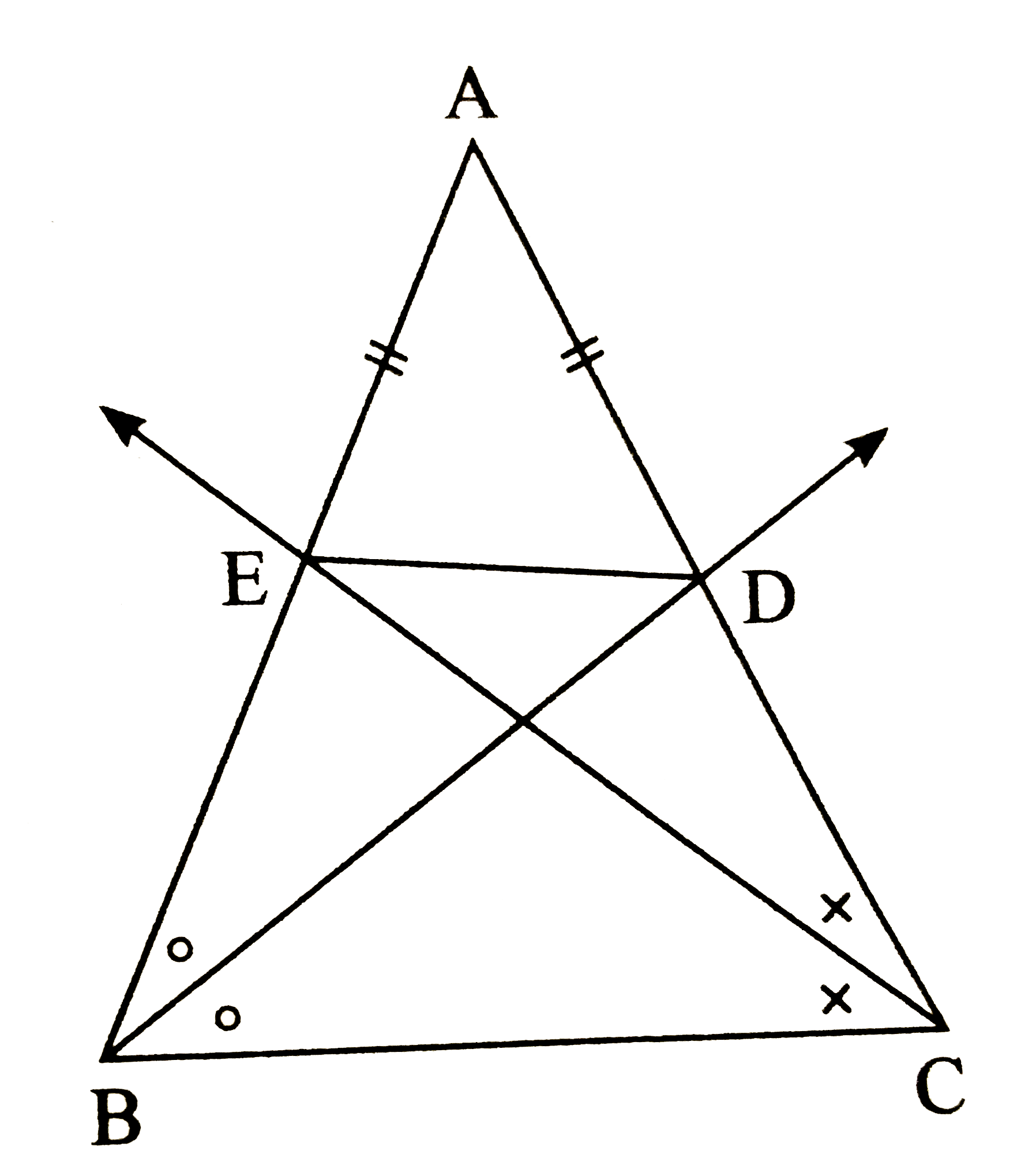
Step by step video & image solution for In the figure, seg AB~= seg AC, ray CE bisects /_ACB , ray BD bisects /_ABC. Prove that ray ED|| side BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

In the given figure, $A B ∣ ∣ E C, A B = A C$ and AE bisects $∠ D A C$ . Prove that:
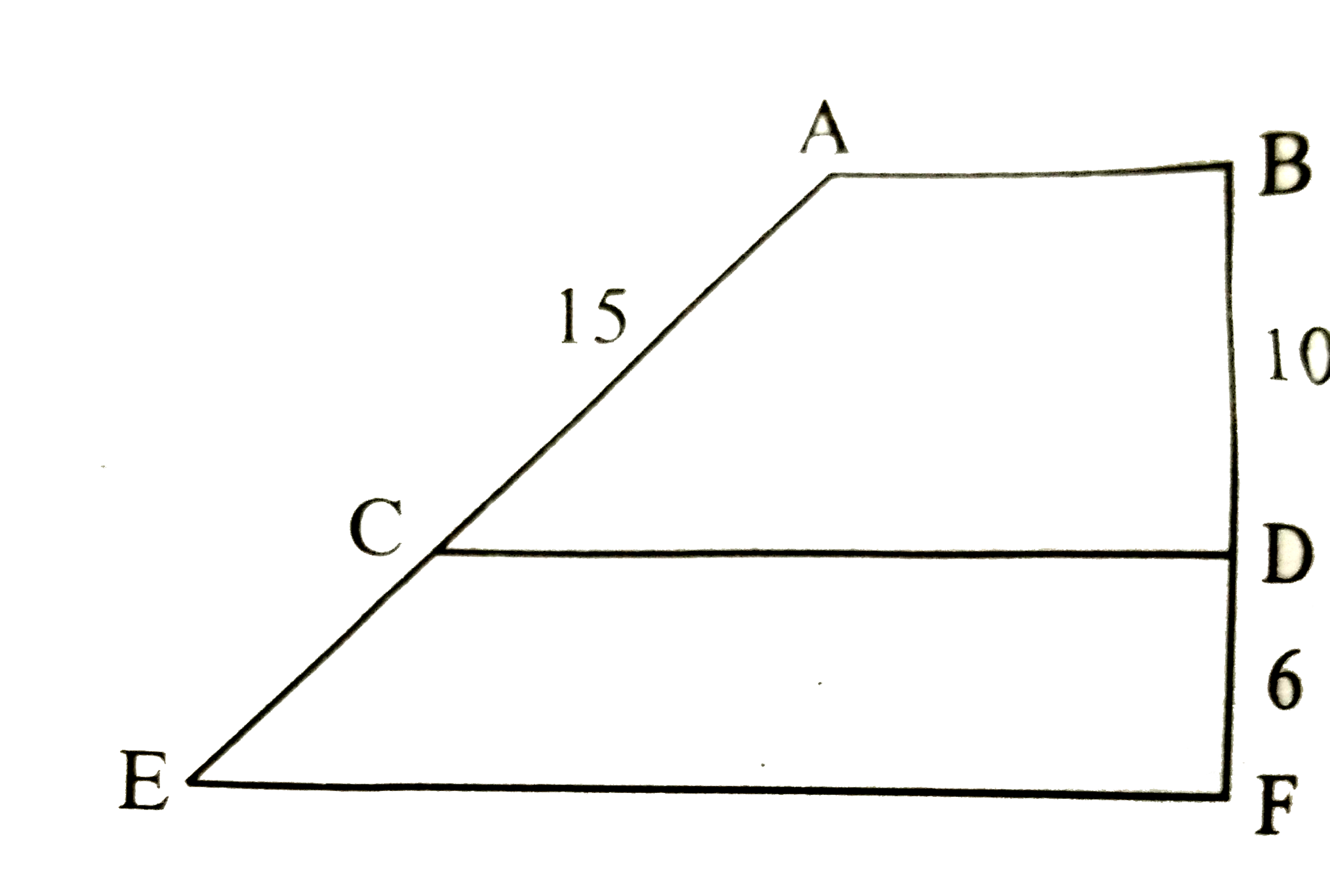
View Solution
In the figure, seg $A B ∣ ∣$ seg $C D ∣ ∣$ seg $E F$ $A C = 1.5$ , $B D = 10$ , $D F = 6$ then $A E = ?$

View Solution
In the given figure, $Δ A B C$ is an isosceles triangle in which AB=AC and AE bisects $∠ C A D$ . Prove that $A E ∣ ∣ B C$ .
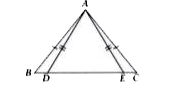
View Solution
In $Δ A B C$ ,ray BD bisects $∠ A B C$ and ray CE bisects $∠ A C B$ . If seg AB $≅$ seg AC, then prove that ED $| |$ BC.
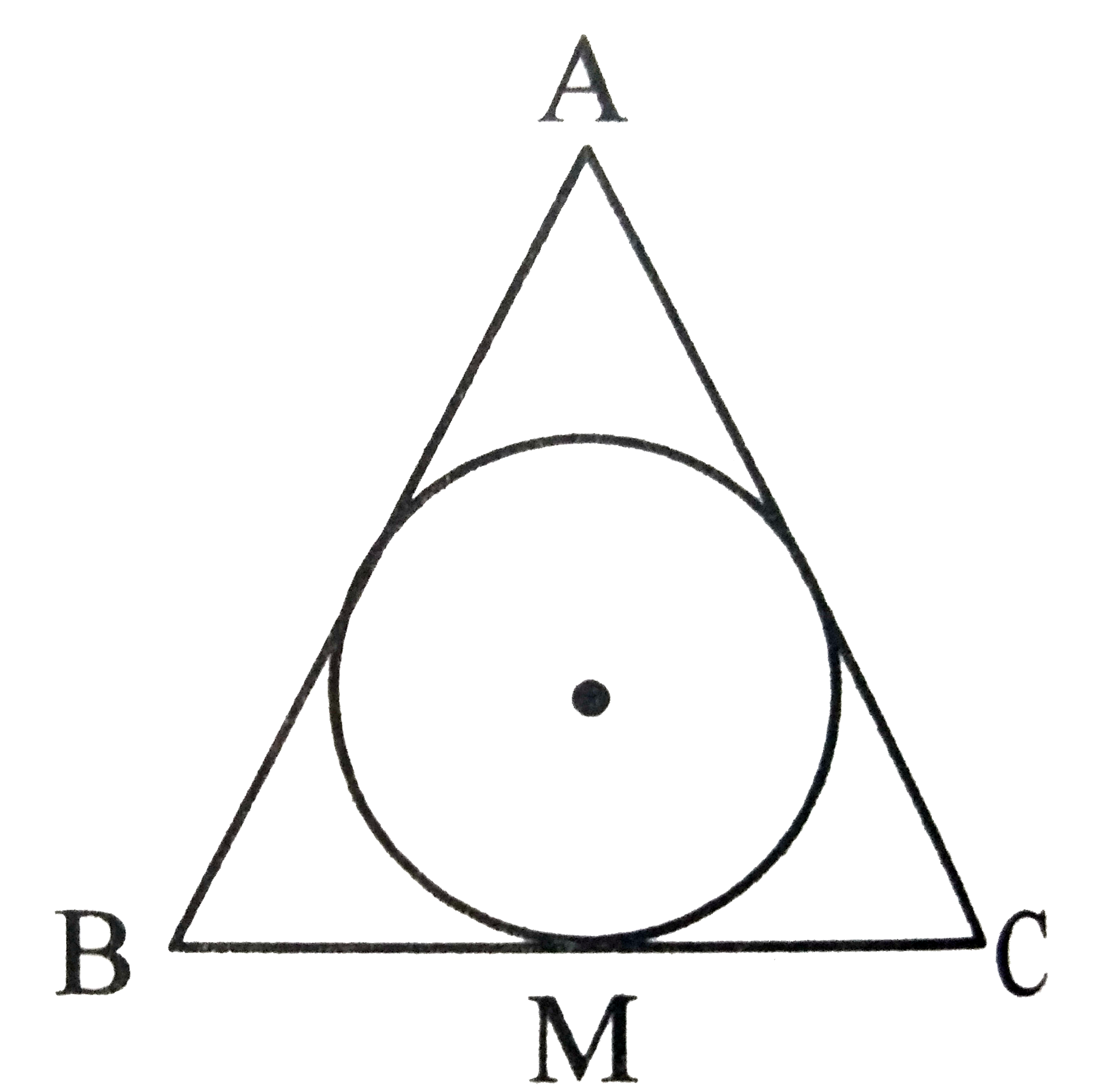
View Solution
In the adjoining figure, the circle is the incircle of isosceles $Δ A B C$ , where seg AB $=$ seg AC. Prove that M bisects BC.

View Solution
In the given figure, ray AE $∣ ∣$ ray BD, ray AF is the bisector of $∠ E A B$ and ray BC is the bisector of $∠ A B D$ . Prove that lineAF $∣ ∣$ line BC.

View Solution
Draw seg AB of length 5.7 cm and bisect it.
View Solution
$B D a n d C E$ are bisectors of $∠ B a n d ∠ C$ of an isosceles $A B C$ with $A B = A C$ . Prove that $B D = C E$
View Solution
In the given figure, AB = AC and AD = AE. Prove that:
BD = CE

View Solution
In the adjoining figure,seg DE $| |$ side AC and seg DC $| |$ side AP.
Prove that $\frac{B E}{E C} = \frac{B C}{C P}$ .

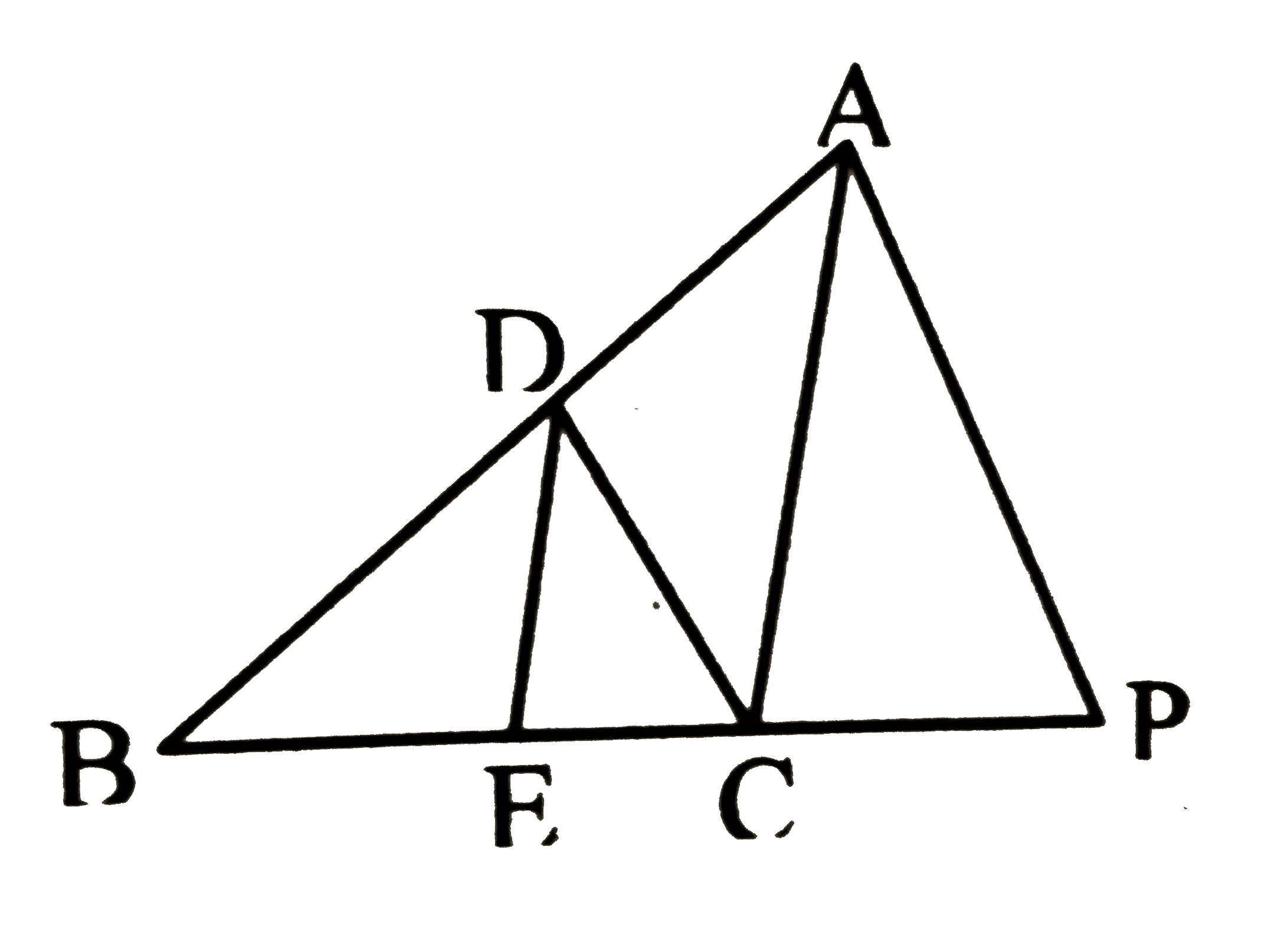
View Solution

In the figure, seg AB≅ seg AC, ray CE bisects ∠ACB , ray BD bisects ∠ABC. Prove that ray ED∣∣ side BC.

Similar Questions

Recommended Questions

In the figure, seg $A B ≅$ seg $A C$ , ray $C E$ bisects $∠ A C B$ , ray $B D$ bisects $∠ A B C$ . Prove that ray $E D ∣ ∣$ side $B C$ .