In the adjoining figure, the circle is the incircle of isosceles , where seg ABseg AC. Prove that M bisects BC.
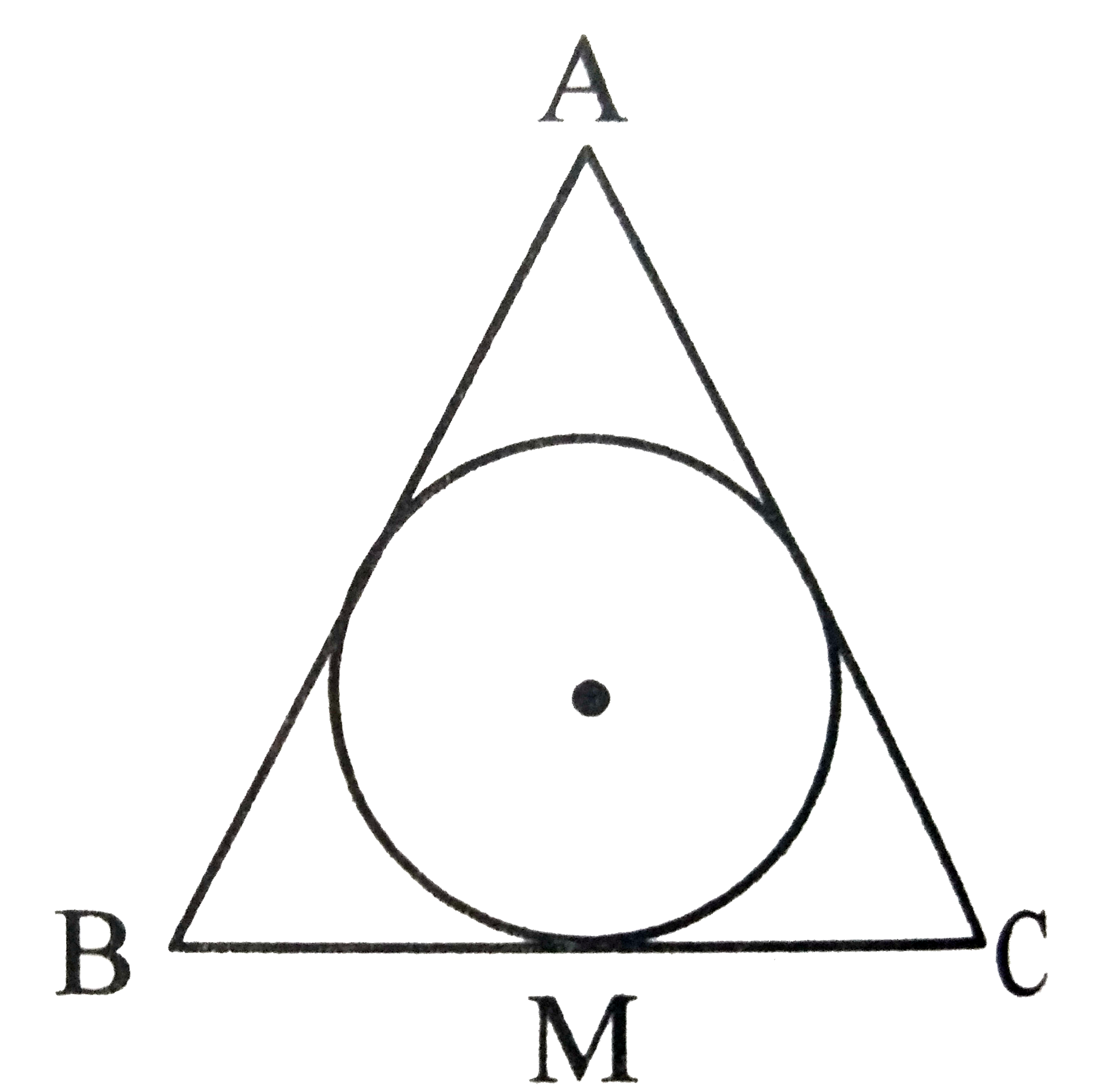
Step by step video & image solution for In the adjoining figure, the circle is the incircle of isosceles DeltaABC, where seg AB=seg AC. Prove that M bisects BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment9videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question25videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
In the adjoining figure, BC = ED, then, prove that ΔABC≅ΔFDE.
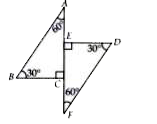 View Solution
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
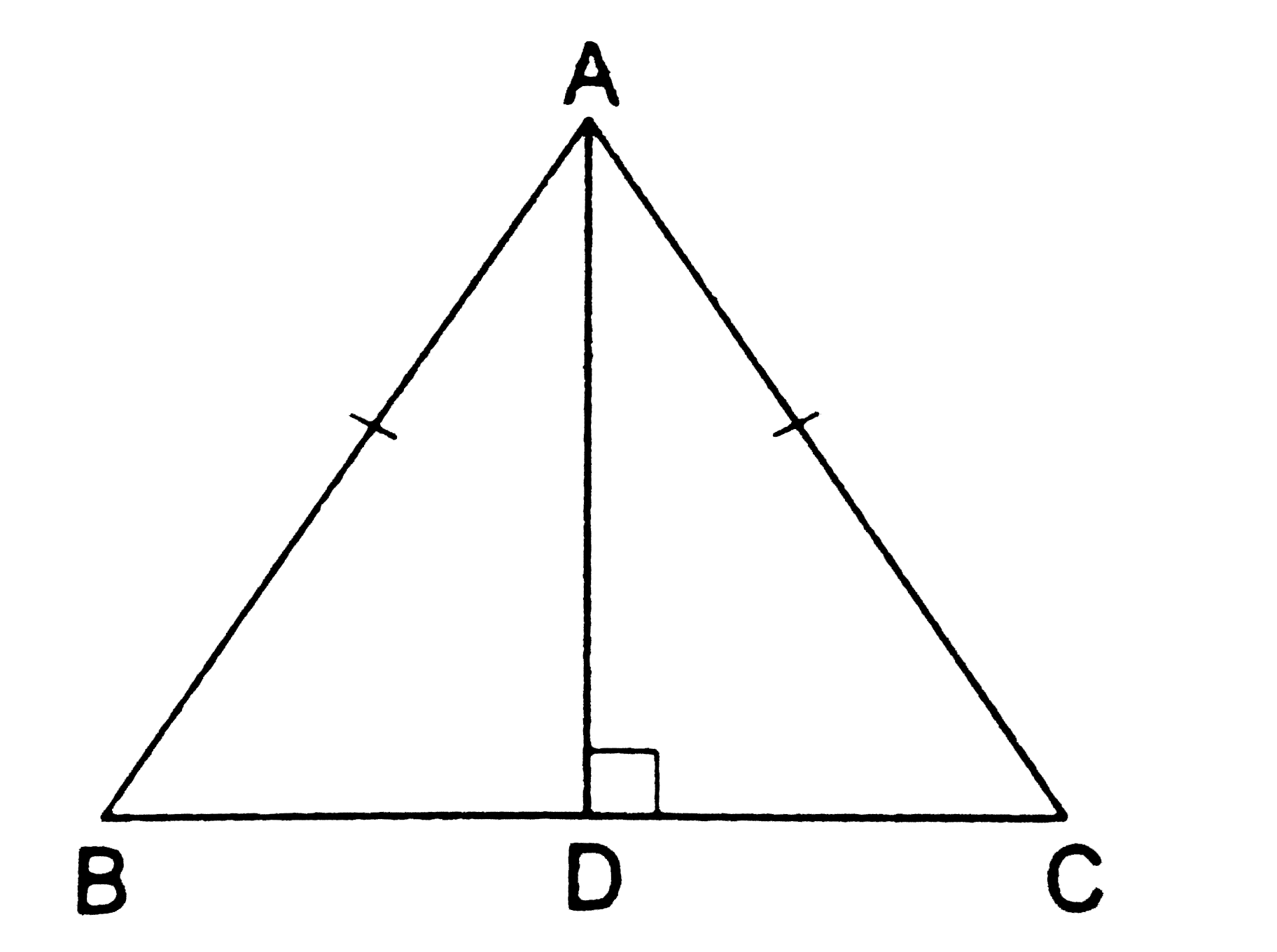 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
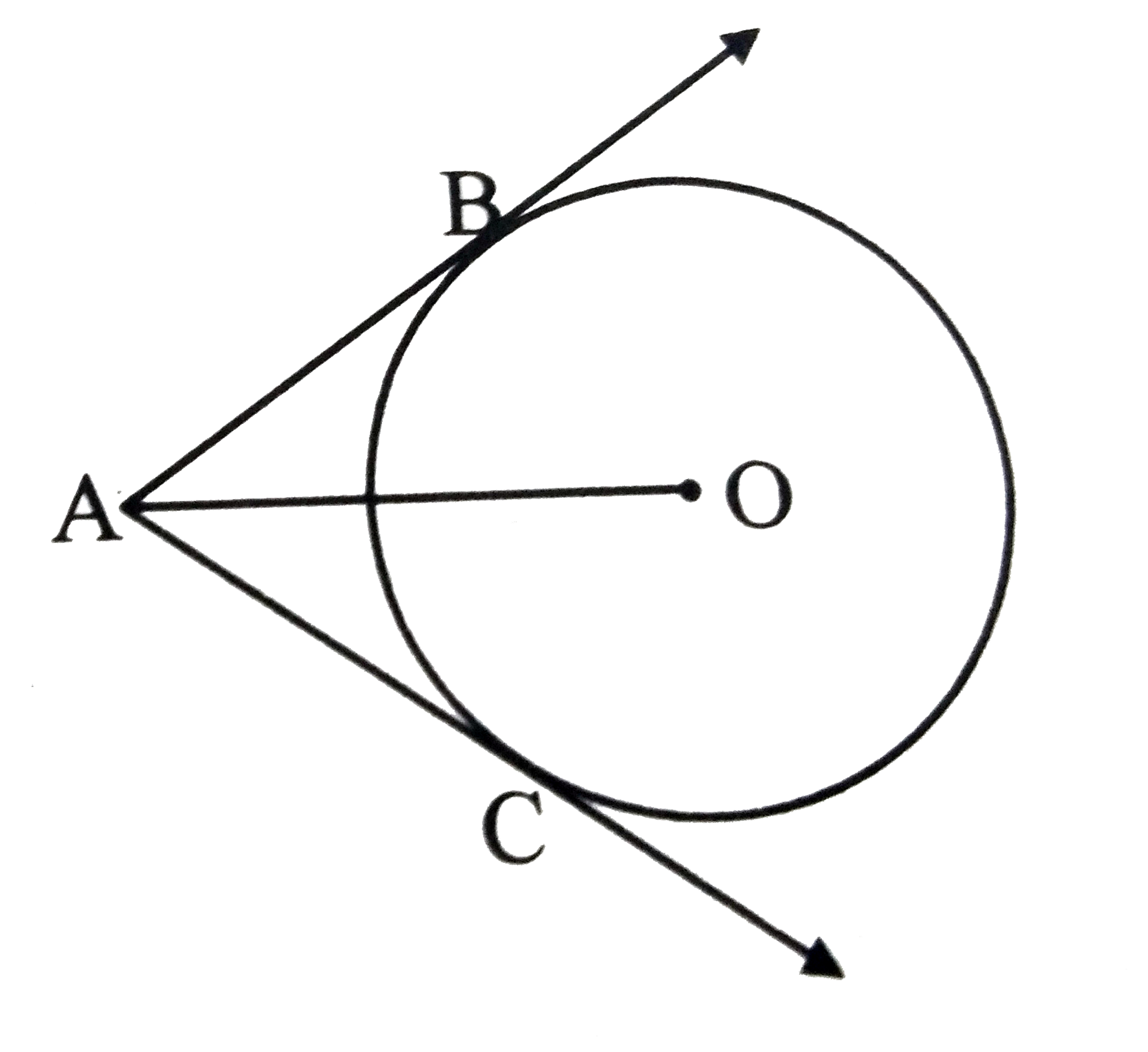 View Solution
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. If BM⊥ACandCN⊥AB, prove that:
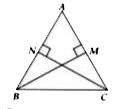
BM = CNView SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
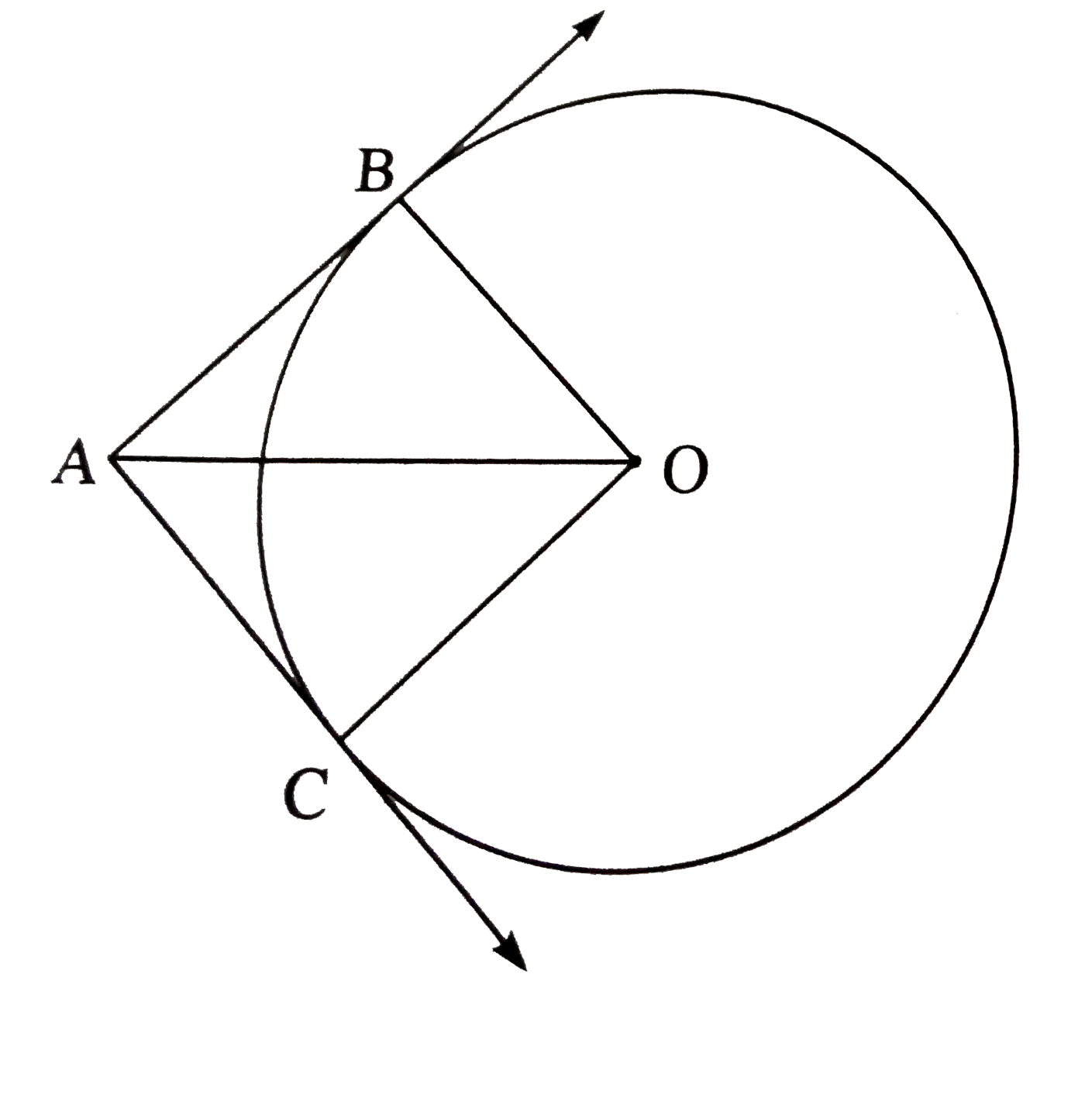 View Solution
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
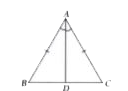
ΔADB≅ΔADCView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CDView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
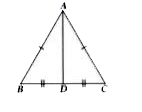 Prove that:
Prove that:
ΔADB≅ΔADCView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
 Prove that:
Prove that:
∠BAD=∠CADView SolutionIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View Solution

