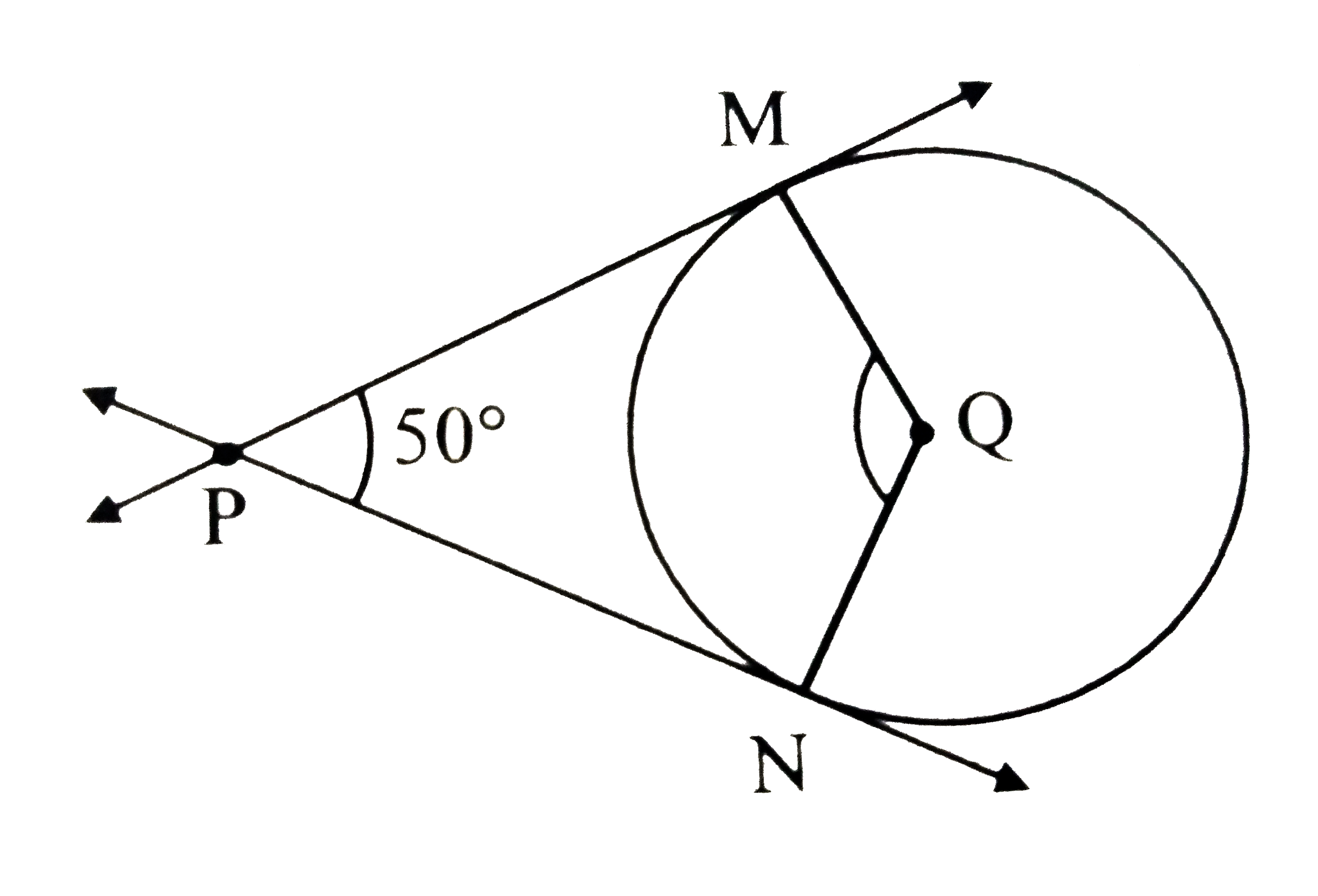
In the figrure, Q is the centre of the circle and PM and PN are tangent segments to the circle. If ∠MPN=40∘, find ∠MQN
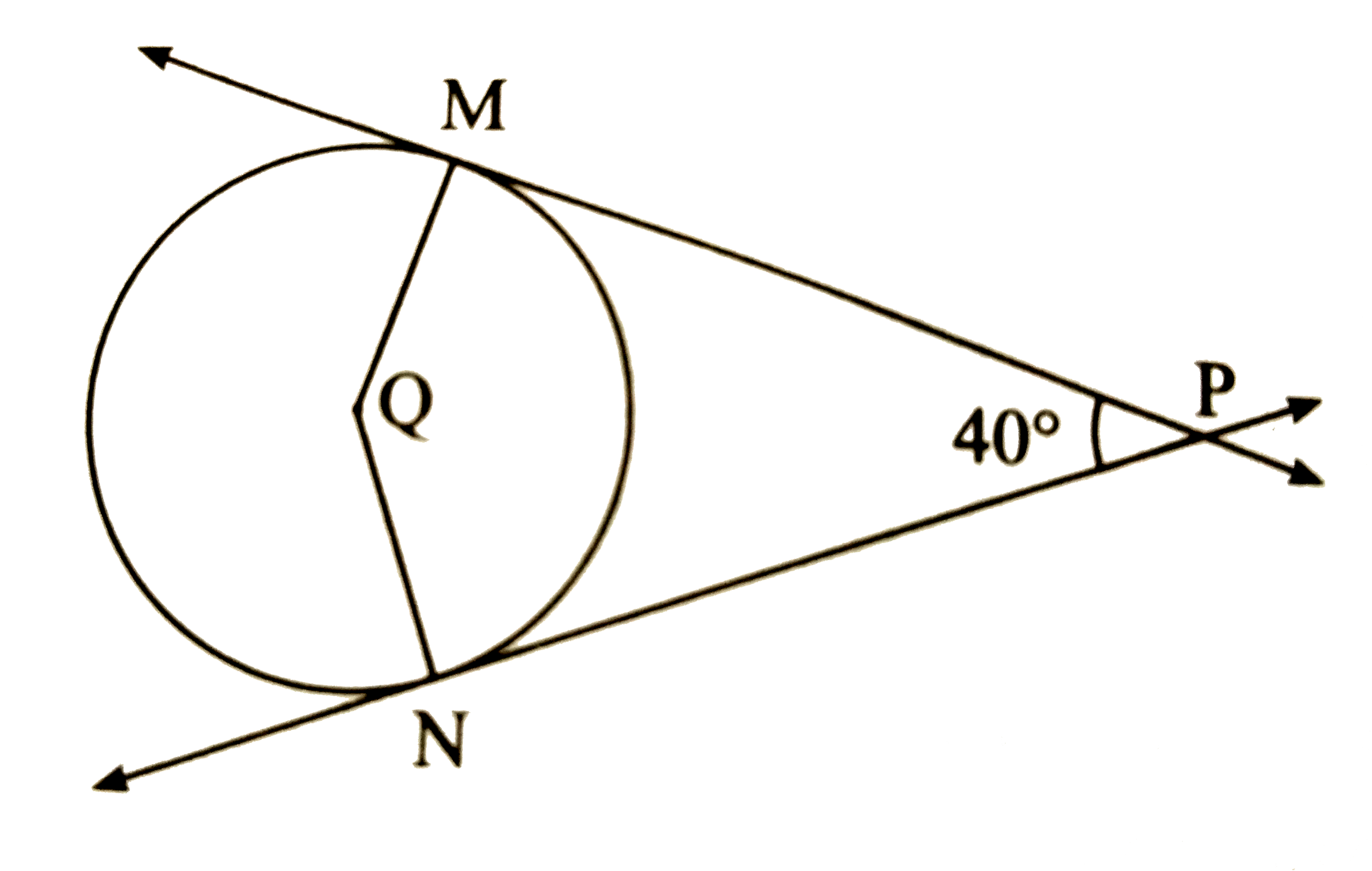
The correct Answer is:∠MQN=140∘
Step by step video & image solution for In the figrure, Q is the centre of the circle and PM and PN are tangent segments to the circle. If /_ MPN = 40^(@), find /_ MQN by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.4
12 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.5
8 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.2
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
ARectangleBSquareCCyclicDNone of these
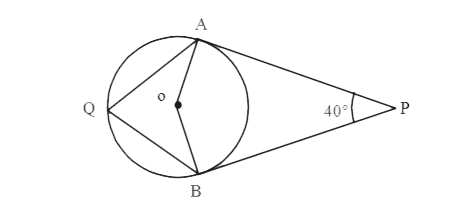
In the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
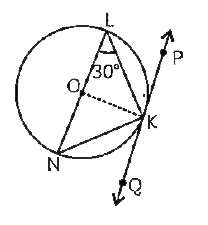
View SolutionIn the figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
View SolutionIn the given figure, O is the centre of the circle. PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
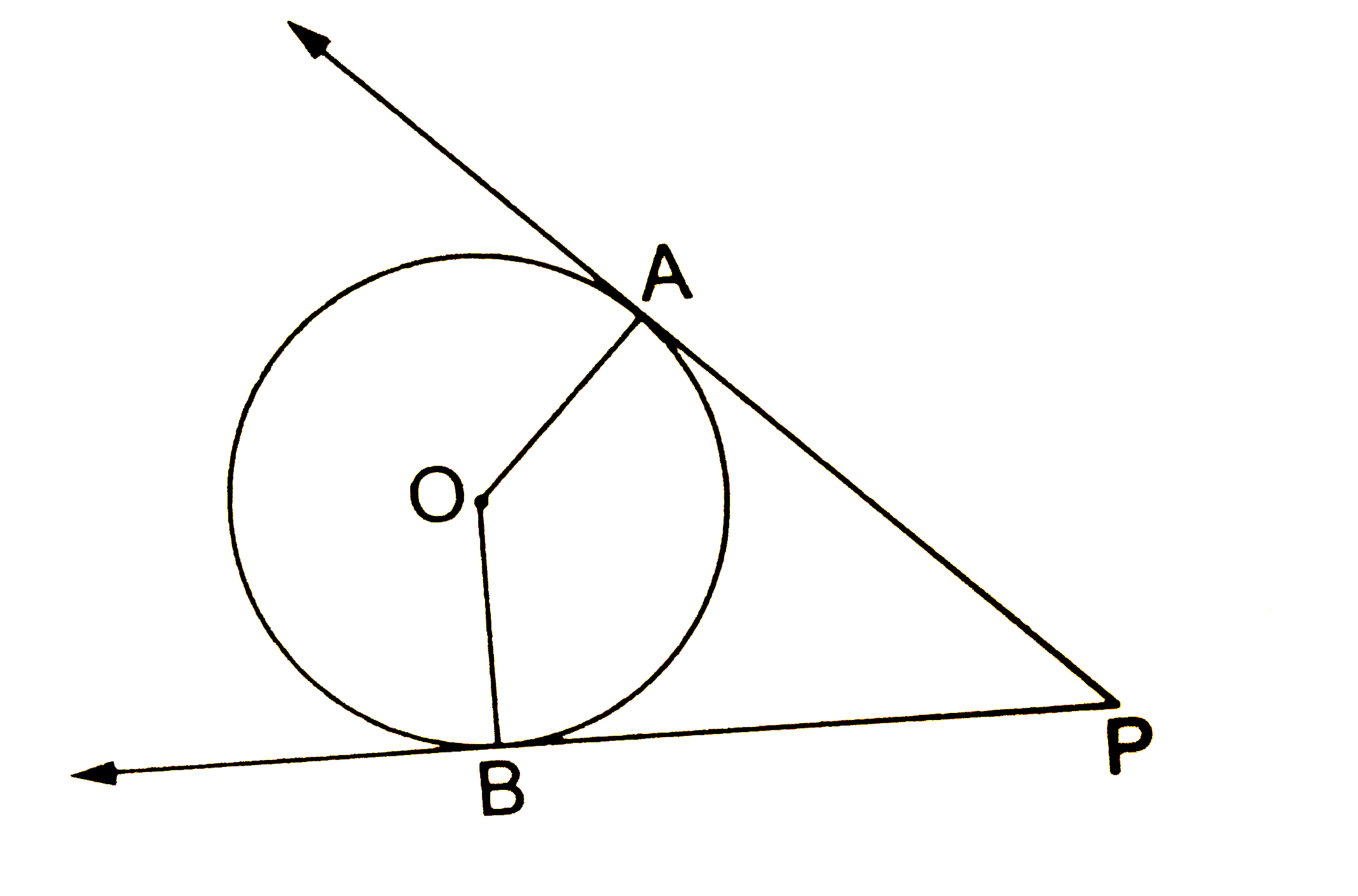
View SolutionIn given figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.

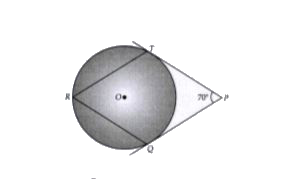
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
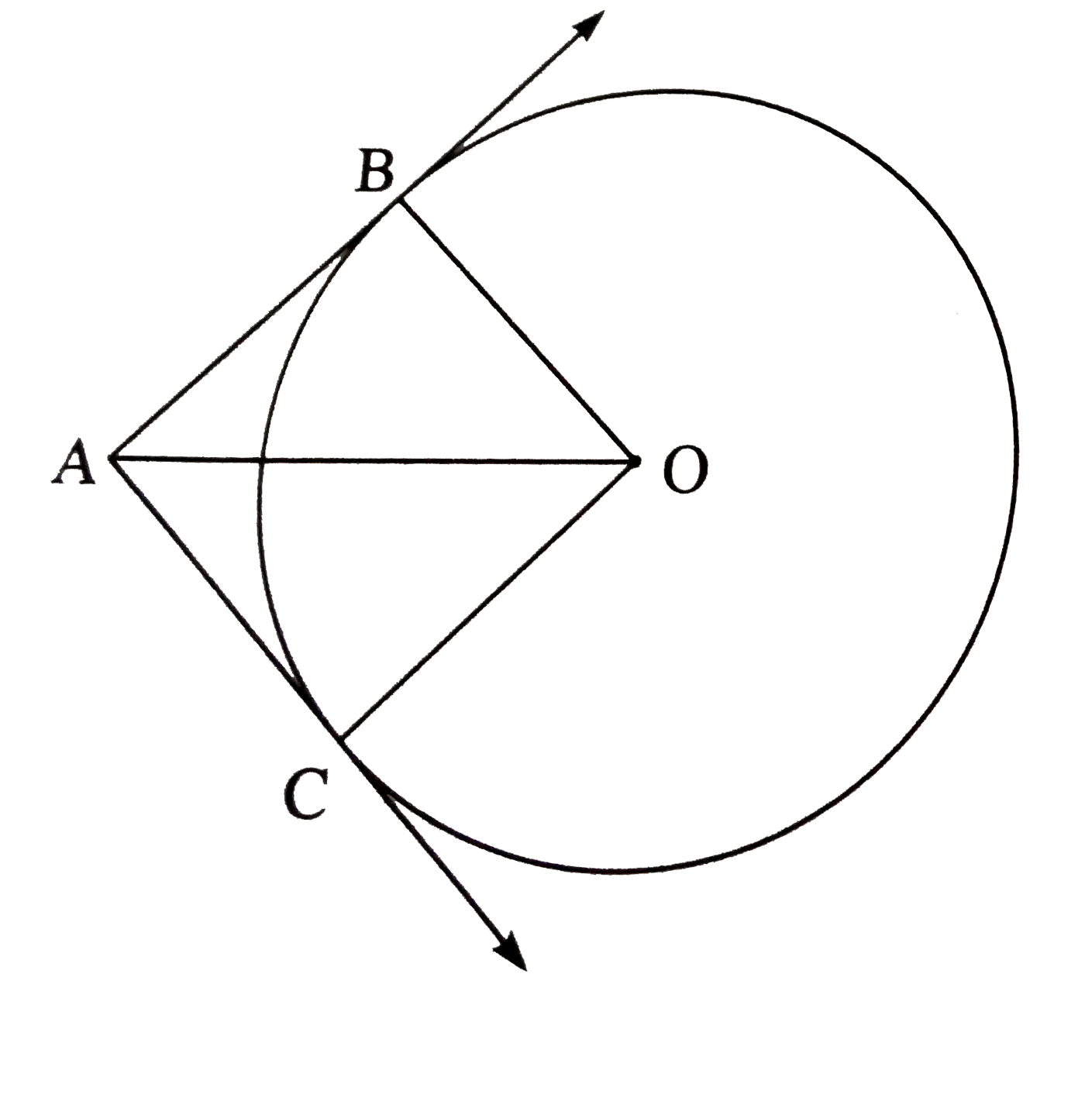
View SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
View SolutionO is the centre of the circle. OP = 5 and OT = 4, and AB = 8. The line PT is a tangent to the circle. Find PB

View Solution