The maximum speed with which a vehicle can be safely driven along curved road of radius r, banked at angle $θ$ is

Video Solution

Text Solution

Verified by Experts

Consider a car taking a left turn along a road of radius r banked at an angle $θ$ for a designed optimum speed v. Let m be the mass of the car. In general, the forces acting on the car are
(a) its weight $- \to m g$ , acting vertically down
(b) the normal reaction of the road $\to N$ , perpendicular to the road surface.
(c ) the frictional force ${\to f}_{s}$ along the inclined surface of the road.

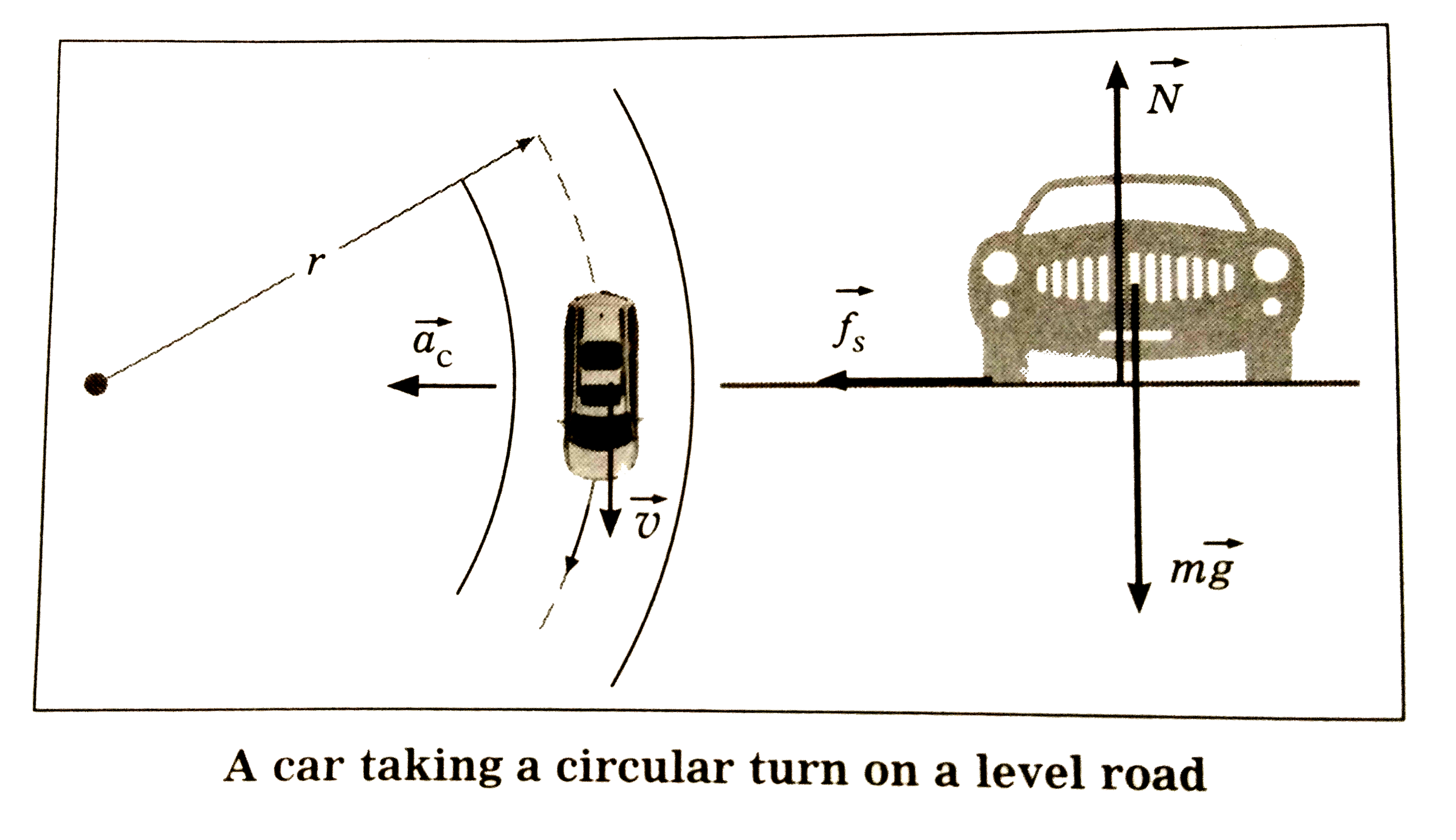
If $μ_{s}$ is the coefficient of static friction between the tyres and raod, $f_{s} = μ_{s} N$ . If the car is driven fast enough, at a speed greater than the optimum speed v, it may skid up the incline so that $\to f_{s}$ is down the incline.
Resolve $\to N$ and $\to f_{s}$ into (i) $cos θ$ vertically up and $f_{s} sin θ$ vertically down (ii) $N sin θ$ and $f_{s} cos θ$ horizontally towards the centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components $N sin θ$ and $f_{s} cos θ$ together provide the necessary centripetal force, and $N cos θ$ balances the sum $m g + f_{s} sin θ$ . If $v_{max}$ is the maximum safe speed of the car (without skidding),
$(m v_{max}^{2}) = N sin θ + f_{s} cos θ + μ_{s} N cos θ$
$= N (sin θ + μ_{s} cos θ) ... (1)$
and $N cos θ = m g + f_{s} sin θ = m g + μ_{s} N sin θ$
$∴ m g = N (cos θ - μ_{s} sin θ) ... (2)$
Dividing Eq. (1) by Eq. (2),
$\frac{m v_{max}^{2} / r}{m g} = \frac{N (sin θ + cos θ)}{N (cos θ - μ_{s} sin θ)}$
$∴ \frac{v_{max}^{2}}{r g} = \frac{sin θ + μ_{s} cos θ}{cos θ - μ_{s} sin θ} = \frac{tan θ + μ_{s}}{1 - μ_{s} tan θ}$
$∴ v_{max} = \sqrt{\frac{r g (tan θ + μ_{s})}{1 - μ tan θ}} ... (3)$
At the optimum speed, the friction between the car tyres and the road surface is not called into play. Hence, by setting $μ_{s} 0$ in Eq. (3), the optimum speed of a car on a banked circular road is
$v = \sqrt{r g tan θ} ... (4)$

Updated on:21/07/2023