Assuming the expression for the MI of a unifrom solid sphere about its diameter, obtain the expression for its moment of inertia about a tangent.
Step by step video & image solution for Assuming the expression for the MI of a unifrom solid sphere about its diameter, obtain the expression for its moment of inertia about a tangent. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Kinetic Theory of Gases and Radiation
5 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - COMMUNICATION SYSTEMS
3 Videos
- DERIVATIONS-IIBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IIEXERCISE - Assignments
9 Videos
Similar Questions
Knowledge Check
If moment of inertia of a solid sphere of mass 5kg about its diameter is 50kgm2 . Its moment of inertia about its tangent in kg m2 is
A260B250C240D175If temperature increases, the moment of inertia of a solid sphere about its diameter
AincreasesBdecreasesCremains unchangedDbecomes negativeThe moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is
A25Kgm2B50kgm2C70kgm2D80kgm2
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionThe moment of inertia of a sphere is 40 kg-m2 about its diametric axis. Determine the moment of inertia about any tangent.
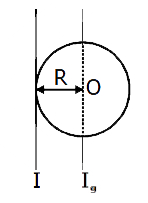
View SolutionState the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
View SolutionState the expression for the MI of a thin ring about a transverse axis through its centre. Hence, derive the expression for the MI of the ring about its tangent perpendicular to the plane.
View SolutionObtain an expression for moment of inertia of a uniform circular disc about a diameter of the disc.
View Solution
