Question

Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is

Explanation

Let M be the mass of a thin ring of radius R. Let `I_(CM)` be the moment of inertia (MI) of the ring about its transverse symmetry axis. Then,
`I_(CM)=MR^(2)`
(1) MI about a diameter : Let x and y-axes be along two perpendicular diameters of the ring as shown in Fig. Let `I_(x) I_(y)` and `I_(z)` be the moments of inertia of the ring about the x,y and z axes, respectively.
Both `I_(x)` and `I_(y)` represent the moment of inertia of the ring about its diameter and, by symmetry, the MI of the ring about any diameter is the same.

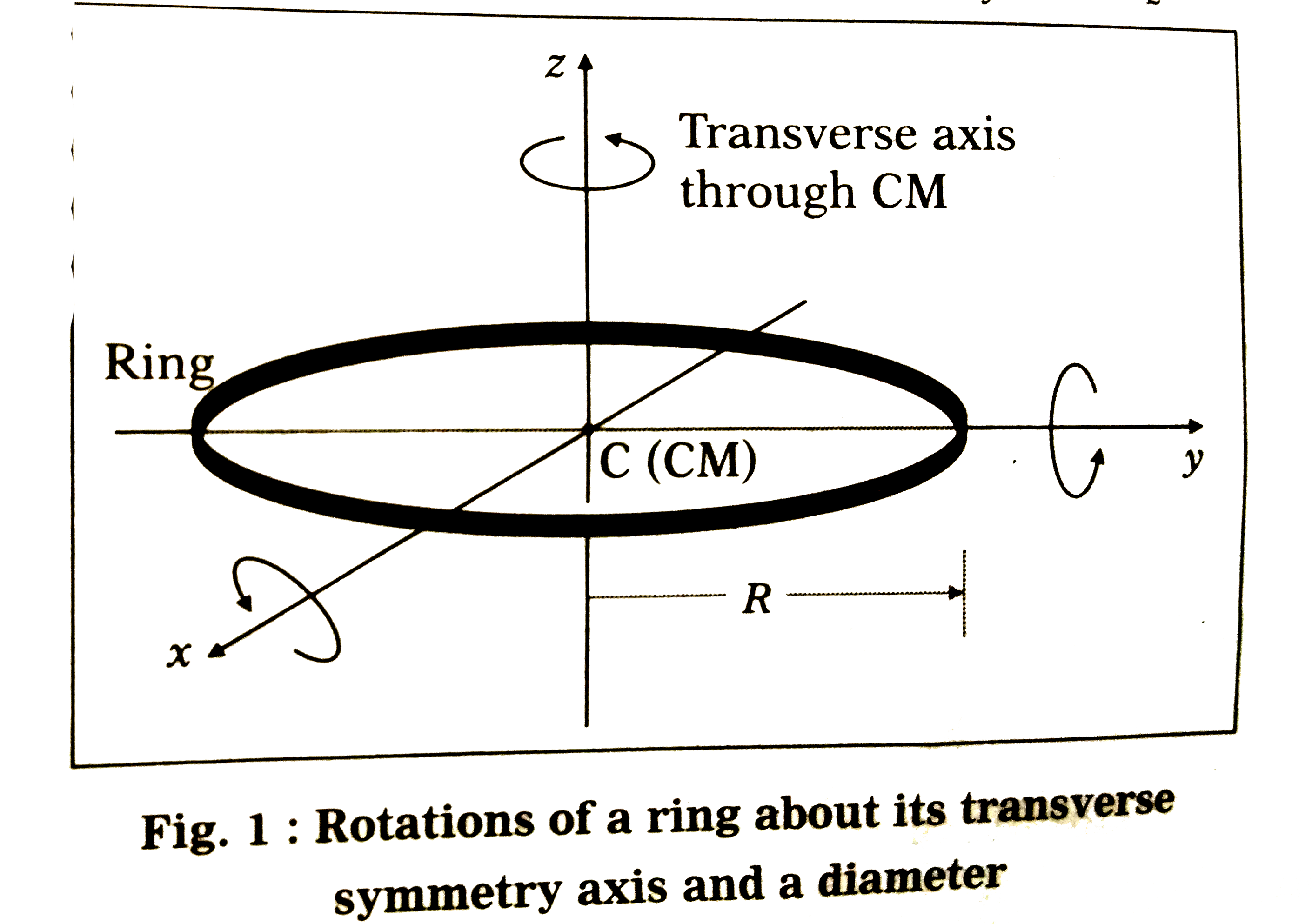
`:. I_(x)=I_(y)" "`......(2)
Also, `I_(z)` being the MI of the ring about its transverse symmetry axis,
`I_(z)=I_(CM)=MR^(2)" "`.......(3)
By the theorem of perpendicular axes,
`I_(z)=I_(x)+I_(y)=2I_(x)""`........(4)
`:. 2I_(x)=MR^(2)`
or `I_(x)=(1)/(2)MR^(2)" "`........(5)
(2) MI about a tangent in its plane : Let I be its MI about an axis in plane of the ring, i.e., parallel to a diameter, and tangent to it. Here, h=R and `I_(CM)=I_(x)=(1)/(2)MR^(2)`.

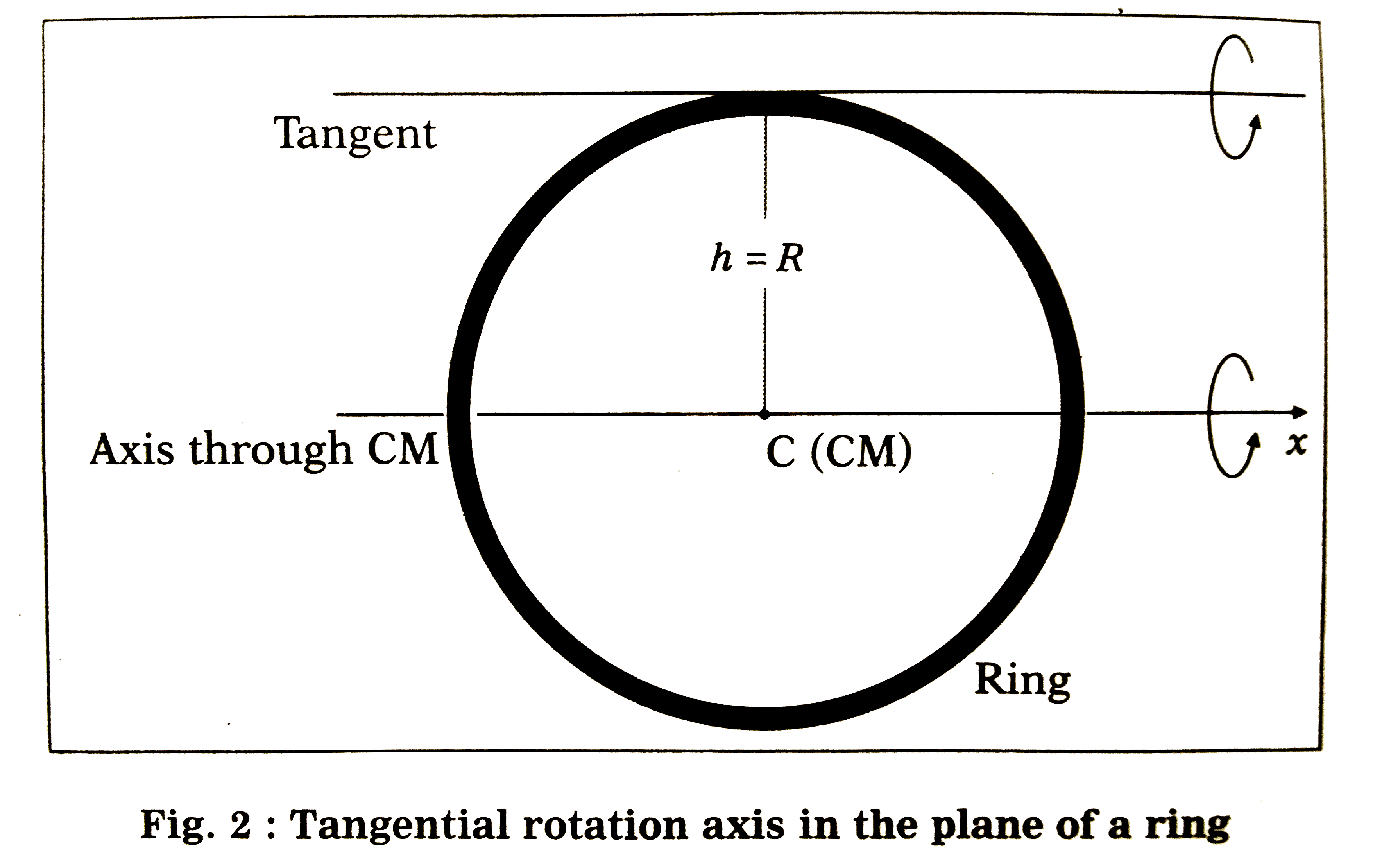
By the theorem of parallel axis,
`I=I_(x)+Mh^(2)`
`=(1)/(2)MR^(2)+MR^(2)=(3)/(2)MR^(2)" "`.....(6)