In the following figure, PR and SQ are chords, of the circle with centre O, intersecting at T and TQ=x,TP=y then show that (TS+TR):(TS−TR)=(x+y):(y−x)
Video Solution
|
Answer
Step by step video & image solution for In the following figure, PR and SQ are chords, of the circle with centre O, intersecting at T and TQ=x, TP=y then show that (TS+TR):(TS-TR)=(x+y):(y-x) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘In the figure, TP and TQ are tangents drawn to the circle with centre at O. If ∠POQ=115∘ then ∠PTQ is:
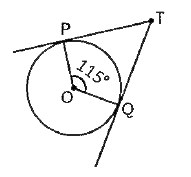 A115∘B57.5∘C55∘D65∘
A115∘B57.5∘C55∘D65∘O is the centre of the circle x and y respectively equal.
 A38∘,45∘B35∘,62∘C62∘,35∘D46∘,38∘
A38∘,45∘B35∘,62∘C62∘,35∘D46∘,38∘
In the given figure , if TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘ , then ∠PTQ is equal to
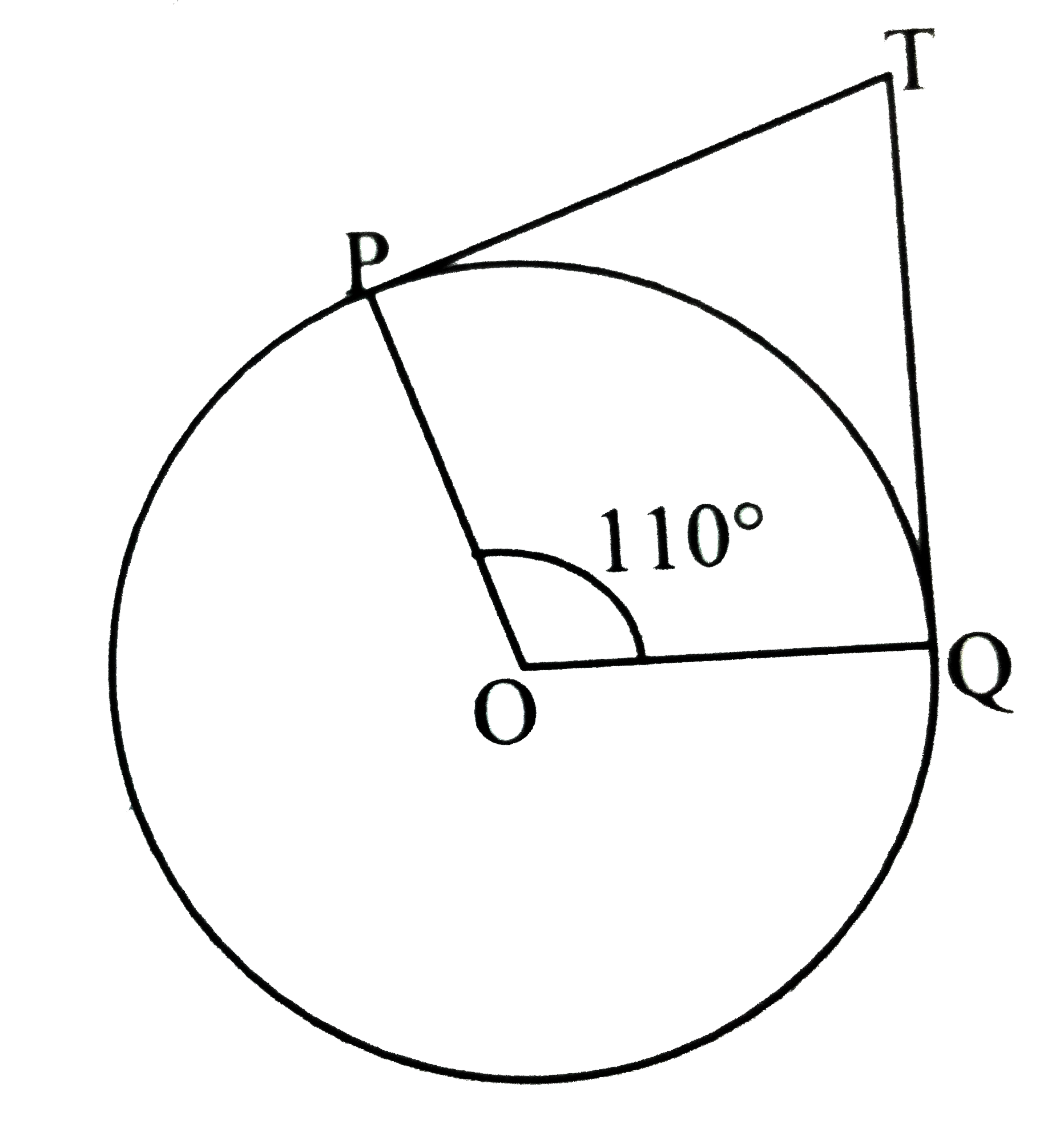
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View Solution

