If TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
To solve the problem, we need to find the angle ∠PTQ given that ∠POQ=110∘ and TP and TQ are tangents to the circle at points P and Q respectively.
1. Identify the Given Information:
- ∠POQ=110∘
- TP and TQ are tangents to the circle.
2. Use the Property of Tangents:
- The tangent at any point on a circle is perpendicular to the radius at that point. Therefore:
- ∠OPT=90∘ (since TP is tangent at point P)
- ∠OQT=90∘ (since TQ is tangent at point Q)
3. Consider Quadrilateral OPTQ:
- In quadrilateral OPTQ, the sum of all interior angles is 360∘.
- Thus, we can write the equation:
∠OPT+∠PTQ+∠OQT+∠POQ=360∘
4. Substitute the Known Angles:
- Substitute the values we know:
90∘+∠PTQ+90∘+110∘=360∘
5. Simplify the Equation:
- Combine the known angles:
90+90+110=290∘
- Therefore, the equation becomes:
∠PTQ+290∘=360∘
6. Solve for ∠PTQ:
- Rearranging gives:
∠PTQ=360∘−290∘=70∘
Final Answer:
Thus, ∠PTQ=70∘.
---
- ∠POQ=110∘
- TP and TQ are tangents to the circle.
- The tangent at any point on a circle is perpendicular to the radius at that point. Therefore:
- ∠OPT=90∘ (since TP is tangent at point P)
- ∠OQT=90∘ (since TQ is tangent at point Q)
- In quadrilateral OPTQ, the sum of all interior angles is 360∘.
- Thus, we can write the equation:
∠OPT+∠PTQ+∠OQT+∠POQ=360∘
- Substitute the values we know:
90∘+∠PTQ+90∘+110∘=360∘
- Combine the known angles:
90+90+110=290∘
- Therefore, the equation becomes:
∠PTQ+290∘=360∘
- Rearranging gives:
∠PTQ=360∘−290∘=70∘
Thus, ∠PTQ=70∘.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.1
2 Videos
- CIRCLESBOOK - NCERT ENGLISHCHAPTER - CIRCLESEXERCISE - SOLVED EXAMPLES
3 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions
65 Videos
- CONSTRUCTIONSBOOK - NCERT ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
7 Videos
Similar Questions
In the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (a) 67o (b) 134o (c) 44o (d) 46o
View SolutionIn Fig. 10.96, if TP and TQ are tangents drawn from an external points T to a circle with centre O such that ∠TQP=60o , then ∠OPQ= (FIGURE) 25o (b) 30o (c) 40o (d) 60o
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
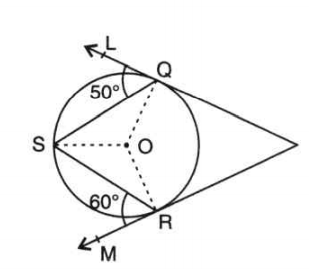
View SolutionIn the given figure, PQL and PRM are two tangents to the circle with centre O at the point Q and R respectively. If S is a point on the circle such that angle SQL = 50° and sk... o angle SRM = 60°. Find the reflex angle QOR.
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80o then ∠POA is equal to :
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View Solution
