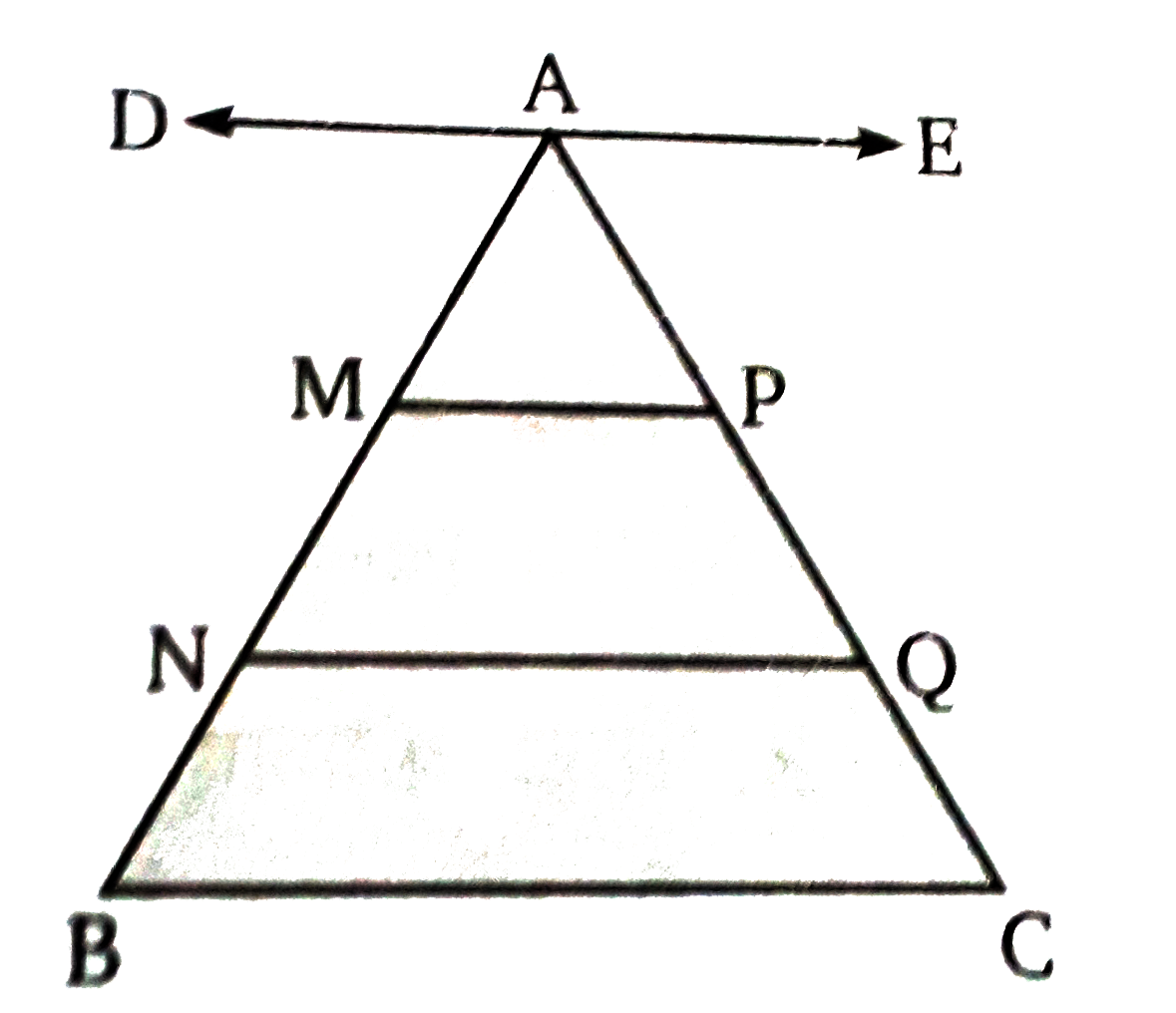
त्रिभुज ABC में भुजा AB को बिन्दु M व N तीन बराबर भागों में बाँटते है। रेखाखण्ड MP व NQ दोनों BC के समान्तर है और AC को क्रमशः P तथा Q पर मिलते है। सिद्ध कीजिए की P व Q भुजा AC को तीन बराबर भागो में बांटते है।
दिया है एक त्रिभुज ABC जिसमे M व N,AB पर दो बिन्दु इस प्रकार है की AM=MN=NB रेखाखण्ड MNवNQ दोनों BC के समान्तर है।
सिद्ध करना है AP=PQ=QC
उपपत्ति DAE∣∣BC तथा MP व NQ दोनों BC के समान्तर है। इसलिए DE,MP व NQ तीनों समान्तर रेखाएँ है। तिर्यक रेखा समान्तर रेखाओं DE,MP व NQ पर क्रमशः A,M व N प्रतिच्छेद करती है तथा AM=MN (दिया है)
इसलिए इन तीनों रेखाओं DAE,MP व NQ द्वारा तिर्यक रेखा पर बने अन्तः खण्ड परस्पर होंगे अथार्त
AP=PQ ...(1)
अब तीन रेखाएँ MP,NQ व BC ले |
∴ तिर्यक रेखा AB समान्तर रेखाओं MP,NQ व BC पर क्रमशः M,N व B इस प्रकार प्रतिच्छेद करती है की MN=NB
इसलिए इन तीनों समान्तर रेखाओं MP,NQ व BC से तिर्यक रेखा AC पर बने अन्तः खण्ड बराबर होंगे
अथार्त PQ=QC ....(2)<br>समीकरण(1)व(2)से<br>AP=PQ=QC
Topper's Solved these Questions
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.1
15 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.2
7 Videos
- घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन BOOK - BALAJI PUBLICATIONCHAPTER - घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
Similar Questions
एक समान्तर चतुर्भुर्ज का के कोण संलग्न (Adjacent) कोण का 23 है । तब समान्तर चतुर्भुर्ज के कोण ज्ञात कीजिए।
View SolutionABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है की EA=AB=BF सिद्ध कीजिए की ED व FC को बढ़ाने पर ये समकोण पर पटिच्छेद करती है ।
View Solutionमंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है । जिसे सांताक्लॉज के चित्र के साथ एक रंगीन कागज़ से ढाका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज़ की कितनी शीटों की आवश्यकता है।
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionकिसी ΔOAB में ∠AOB=90∘ तथा बिन्दु P, Q भुजा AB को समत्रिभाजित करते हैं | सिद्ध कीजिए कि, OP2+OQ2=59AB2.
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solutionदीर्घवृत्त x236+y29=1 की जीवा का समीकरण, जोकि बिन्दु (2, 1) से जाती है, तथा यह बिन्दु जीवा को दो बराबर-बराबर भागों में विभाजित करता है, होगा
View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
View Solutionमरुभूमि में समाज के लिए उपलब्ध पानी को तीन रूपों में बाँटा गया है जिसका पहला रूप है
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionIn a triangle ABC , the sides AB and AC are extended to P and Q respectively. The bisectors of angle PBC and angle QCB intersect at a point R. If angle R= 66^@ , then the measure of angle A is : त्रिभुज ABC में, AB और AC भुजाओं को क्रमशः P और Q तक बढ़ाया जाता है| angle PBC तथा angle QCB के द्विभाजक एक बिंदु R पर मिलते हैं | यदि angle R= 66^@ , है, तो कोण A का मान ज्ञात करें |
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe sides AB and AC of a triangle ABC are extended to P and Q respectively. If the bisectors of angle PBC and angle QCB intersect at O, and angle A=92^@ , then angle BOC is equal to: एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि angle PBC तथा angle QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा angle A=92^@ है, तो angle BOC किसके बराबर है ?
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC ,AD bisects angle A which meets BC at D. If BC = a, AC = b and AB = c, then DC = ? त्रिभुज ABC में, AD कोण A को द्विभाजित करता है जो BC से D पर मिलता है | यदि BC = a, AC = bऔर AB = c है, तो DC = ?
View Solution
