In a △ABC, the sides AB and AC are extended to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at a point R. If ∠R=66∘, then the measure of ∠A is :
त्रिभुज ABC में, AB और AC भुजाओं को क्रमशः P और Q तक बढ़ाया जाता है| ∠PBC तथा ∠QCB के द्विभाजक एक बिंदु R पर मिलते हैं | यदि ∠R=66∘, है, तो कोण A का मान ज्ञात करें |
36∘
24∘
48∘
72∘
To solve the problem, we need to find the measure of angle A in triangle ABC given that the angle R formed by the bisectors of angles PBC and QCB is 66 degrees.
1. Understand the Geometry:
- We have triangle ABC.
- Extend side AB to point P and side AC to point Q.
- The angle bisector of angle PBC meets the angle bisector of angle QCB at point R.
2. Use the Given Information:
- We know that angle R = 66 degrees.
3. Apply the Angle Bisector Theorem:
- There is a well-known result in geometry that states:
∠R=90∘−∠A2
- This means that the angle R formed by the intersection of the angle bisectors can be expressed in terms of angle A.
4. Substitute the Known Value:
- Substitute the value of angle R into the equation:
66∘=90∘−∠A2
5. Rearrange the Equation:
- To isolate ∠A, first subtract 90 degrees from both sides:
66∘−90∘=−∠A2
−24∘=−∠A2
- Multiply both sides by -1:
24∘=∠A2
6. Solve for Angle A:
- Multiply both sides by 2 to find ∠A:
∠A=24∘×2=48∘
Final Answer:
The measure of angle A is 48∘.
---
- We have triangle ABC.
- Extend side AB to point P and side AC to point Q.
- The angle bisector of angle PBC meets the angle bisector of angle QCB at point R.
- We know that angle R = 66 degrees.
- There is a well-known result in geometry that states:
∠R=90∘−∠A2
- This means that the angle R formed by the intersection of the angle bisectors can be expressed in terms of angle A.
- Substitute the value of angle R into the equation:
66∘=90∘−∠A2
- To isolate ∠A, first subtract 90 degrees from both sides:
66∘−90∘=−∠A2
−24∘=−∠A2
- Multiply both sides by -1:
24∘=∠A2
- Multiply both sides by 2 to find ∠A:
∠A=24∘×2=48∘
The measure of angle A is 48∘.
Topper's Solved these Questions
Similar Questions
The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is :
एक त्रिभुज ABC की भुजाएं AB और AC को क्रमशः बिंदु D तथा E तक बढ़ाया जाता है | ∠CBD तथा ∠BCE के समद्विभाजक P पर मिलते हैं | यदि ∠A=72∘ है, तो कोण P का मान ज्ञात करें
View SolutionThe sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View Solution
Knowledge Check
In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
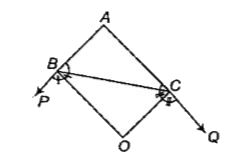 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the aboveThe sides AB and AC of △ABC are produced to points D and E, respectiely. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=82∘, then the measure of ∠P is :
A54∘B60∘C36∘D49∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
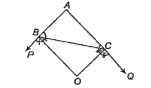 A90∘−12<BACB12(<PBC+<QCB)C90∘+12<BACDNone of the above
A90∘−12<BACB12(<PBC+<QCB)C90∘+12<BACDNone of the above
The sides AB and AC of a △ABC are extended to P and Q respectively. If the bisectors of ∠PBC and ∠QCB intersect at O, and ∠A=92∘, then ∠BOC is equal to:
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि ∠PBC तथा ∠QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा ∠A=92∘ है, तो ∠BOC किसके बराबर है ?
View SolutionThe sides PQ and PR of △PQR are produced to points S and T, respectively. The bisectors of ∠SQR and ∠TRQ meet at U. If ∠QUR=79∘ , then the measure of ∠P is:
त्रिभुज PQR की भुजाओ PQ और QR को क्रमशः S और T तक बढ़ाया जाता है| ∠SQR और ∠TRQ के समद्विभाजक U पर मिलते हैं| यदि ∠QUR=79∘ है, तो कोण P का मान ज्ञात करें |
View SolutionThe sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at O. If the measure of ∠A is 44∘, then what is the measure of 12∠BOC?
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P और Q तक बढ़ाया जाता है | ∠CBP और ∠BCQ के समद्विभाजक O पर मिलते हैं| यदि कोण A का मान 44∘ है, तो 12∠BOC का मान क्या होगा ?
View SolutionIn ∠ABC, AB and AC are produced to points D and E respectively. If the bisector of ∠CBD and ∠BCE meet at a point O and ∠BOC=57∘, then ∠A is equal to :
त्रिभुज ABC में, AB और AC क्रमशः D और E तक बढ़ाये जाते हैं। यदि कोण ∠CBD और ∠BCE के सम द्विभाजक बिंदु O पर मिलते हैं, और ∠BOC=57∘ तो ∠A बराबर है
View SolutionThe sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at R. If the measure of ∠A is 44∘, then what is the measure of 12∠BRC?
त्रिभुज ABC की AB और AC भुजाएं क्रमशः P और Q बनाती हैं। ∠CBP और ∠BCQ के द्विभाजक R पर मिलते हैं। अगर ∠A का माप 44∘ है तो 12∠BRC का माप क्या है?
View Solution
